Example 7.3 Model for Series J Data from Box and Jenkins
This example uses the Series J data from Box and Jenkins (1976). First, the input series X is modeled with a univariate ARMA model. Next, the dependent series Y is cross-correlated with the input series. Since a model has been fit to X, both Y and X are prewhitened by this model before the sample cross-correlations are computed. Next, a transfer function model is fit with no structure on the noise term. The residuals from this model are analyzed; then, the full model, transfer function and noise, is fit to the data.
The following statements read 'Input Gas Rate' and 'Output CO ' from a gas furnace. (Data values are not shown. The full example including data is in the SAS/ETS sample library.)
' from a gas furnace. (Data values are not shown. The full example including data is in the SAS/ETS sample library.)
title1 'Gas Furnace Data';
title2 '(Box and Jenkins, Series J)';
data seriesj;
input x y @@;
label x = 'Input Gas Rate'
y = 'Output CO2';
datalines;
... more lines ...
The following statements produce Output 7.3.1 through Output 7.3.11:
proc arima data=seriesj;
/*--- Look at the input process ----------------------------*/
identify var=x;
run;
/*--- Fit a model for the input ----------------------------*/
estimate p=3 plot;
run;
/*--- Crosscorrelation of prewhitened series ---------------*/
identify var=y crosscorr=(x) nlag=12;
run;
/*--- Fit a simple transfer function - look at residuals ---*/
estimate input=( 3 $ (1,2)/(1) x );
run;
/*--- Final Model - look at residuals ----------------------*/
estimate p=2 input=( 3 $ (1,2)/(1) x );
run;
quit;
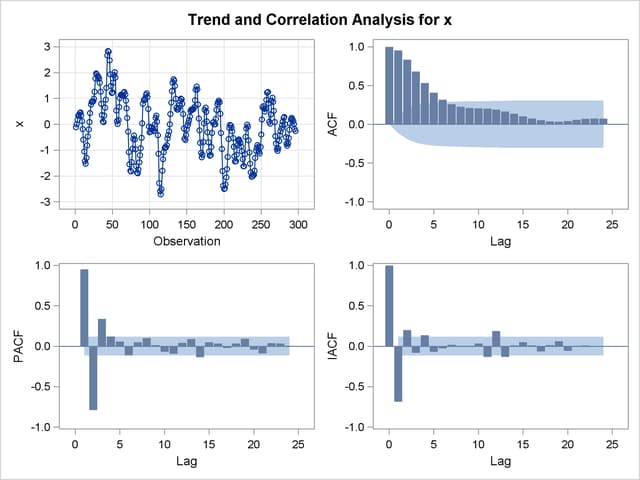
The results of the first IDENTIFY statement for the input series X are shown in Output 7.3.1. The correlation analysis suggests an AR(3) model.
Output 7.3.1
IDENTIFY Statement Results for X
Output 7.3.2
IDENTIFY Statement Results for X: Trend and Correlation
The ESTIMATE statement results for the AR(3) model for the input series X are shown in Output 7.3.3.
Output 7.3.3
Estimates of the AR(3) Model for X
| -0.12280 |
0.10902 |
-1.13 |
0.2609 |
0 |
| 1.97607 |
0.05499 |
35.94 |
<.0001 |
1 |
| -1.37499 |
0.09967 |
-13.80 |
<.0001 |
2 |
| 0.34336 |
0.05502 |
6.24 |
<.0001 |
3 |
| -0.00682 |
| 0.035797 |
| 0.1892 |
| -141.667 |
| -126.906 |
| 296 |
| 1 - 1.97607 B**(1) + 1.37499 B**(2) - 0.34336 B**(3) |
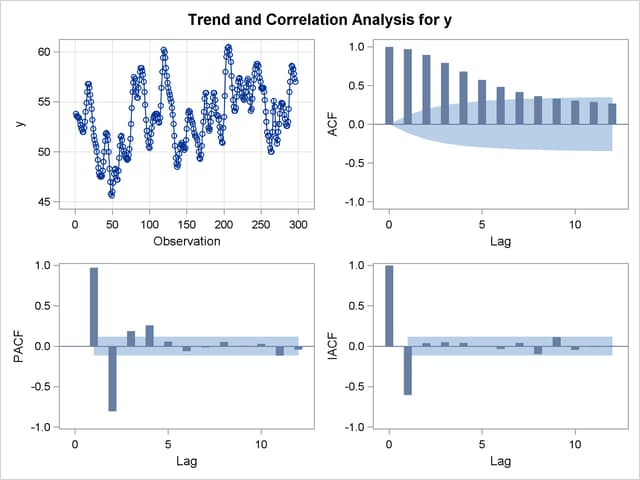
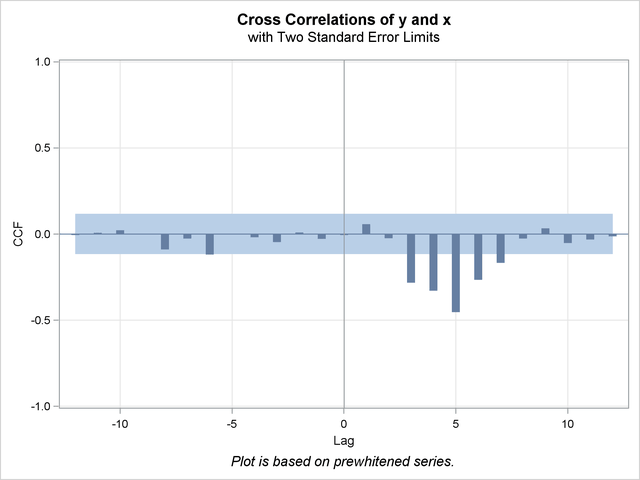
The IDENTIFY statement results for the dependent series Y cross-correlated with the input series X are shown in Output 7.3.4, Output 7.3.5, Output 7.3.6, and Output 7.3.7. Since a model has been fit to X, both Y and X are prewhitened by this model before the sample cross-correlations are computed.
Output 7.3.4
Summary Table: Y Cross-Correlated with X
Both series have been prewhitened.
Output 7.3.5
Prewhitening Filter
| 1 - 1.97607 B**(1) + 1.37499 B**(2) - 0.34336 B**(3) |
Output 7.3.6
IDENTIFY Statement Results for Y: Trend and Correlation
Output 7.3.7
IDENTIFY Statement for Y Cross-Correlated with X
The ESTIMATE statement results for the transfer function model with no structure on the noise term are shown in
Output 7.3.8,
Output 7.3.9, and
Output 7.3.10.
Output 7.3.8
Estimation Output of the First Transfer Function Model
| 53.32256 |
0.04926 |
1082.51 |
<.0001 |
0 |
y |
0 |
| -0.56467 |
0.22405 |
-2.52 |
0.0123 |
0 |
x |
3 |
| 0.42623 |
0.46472 |
0.92 |
0.3598 |
1 |
x |
3 |
| 0.29914 |
0.35506 |
0.84 |
0.4002 |
2 |
x |
3 |
| 0.60073 |
0.04101 |
14.65 |
<.0001 |
1 |
x |
3 |
| 53.32256 |
| 0.702625 |
| 0.838227 |
| 728.0754 |
| 746.442 |
| 291 |
Output 7.3.9
Model Summary: First Transfer Function Model
| -0.5647 - 0.42623 B**(1) - 0.29914 B**(2) |
Output 7.3.10
Residual Analysis: First Transfer Function Model
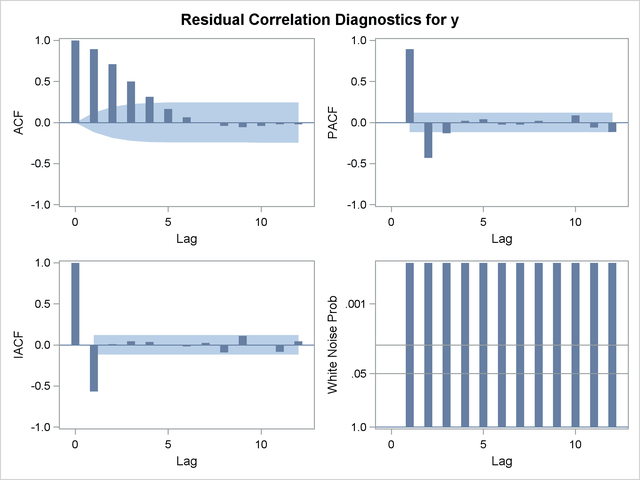
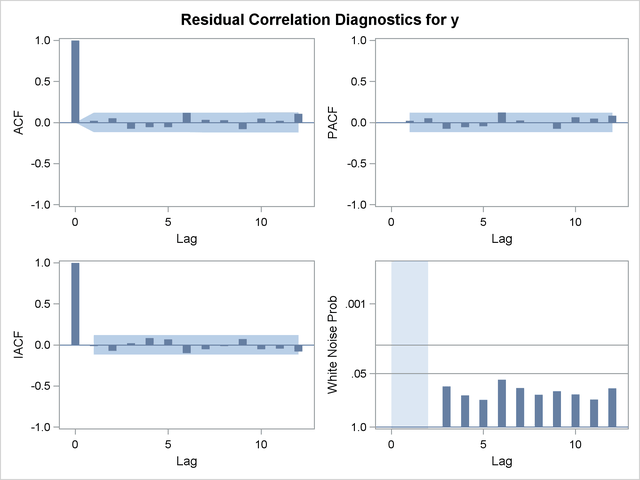
The residual correlation analysis suggests an AR(2) model for the noise part of the model. The ESTIMATE statement results for the final transfer function model with AR(2) noise are shown in Output 7.3.11.
Output 7.3.11
Estimation Output of the Final Model
| 53.26304 |
0.11929 |
446.48 |
<.0001 |
0 |
y |
0 |
| 1.53291 |
0.04754 |
32.25 |
<.0001 |
1 |
y |
0 |
| -0.63297 |
0.05006 |
-12.64 |
<.0001 |
2 |
y |
0 |
| -0.53522 |
0.07482 |
-7.15 |
<.0001 |
0 |
x |
3 |
| 0.37603 |
0.10287 |
3.66 |
0.0003 |
1 |
x |
3 |
| 0.51895 |
0.10783 |
4.81 |
<.0001 |
2 |
x |
3 |
| 0.54841 |
0.03822 |
14.35 |
<.0001 |
1 |
x |
3 |
| 5.329425 |
| 0.058828 |
| 0.242544 |
| 8.292809 |
| 34.00607 |
| 291 |
Output 7.3.12
Residual Analysis of the Final Model
Output 7.3.13
Model Summary of the Final Model
| 1 - 1.53291 B**(1) + 0.63297 B**(2) |
| -0.5352 - 0.37603 B**(1) - 0.51895 B**(2) |
 The Three Stages of ARIMA Modeling Identification Stage Estimation and Diagnostic Checking Stage Forecasting Stage Using ARIMA Procedure Statements General Notation for ARIMA Models Stationarity Differencing Subset, Seasonal, and Factored ARMA Models Input Variables and Regression with ARMA Errors Intervention Models and Interrupted Time Series Rational Transfer Functions and Distributed Lag Models Forecasting with Input Variables Data Requirements
The Three Stages of ARIMA Modeling Identification Stage Estimation and Diagnostic Checking Stage Forecasting Stage Using ARIMA Procedure Statements General Notation for ARIMA Models Stationarity Differencing Subset, Seasonal, and Factored ARMA Models Input Variables and Regression with ARMA Errors Intervention Models and Interrupted Time Series Rational Transfer Functions and Distributed Lag Models Forecasting with Input Variables Data Requirements
 The Inverse Autocorrelation Function The Partial Autocorrelation Function The Cross-Correlation Function The ESACF Method The MINIC Method The SCAN Method Stationarity Tests Prewhitening Identifying Transfer Function Models Missing Values and Autocorrelations Estimation Details Specifying Inputs and Transfer Functions Initial Values Stationarity and Invertibility Naming of Model Parameters Missing Values and Estimation and Forecasting Forecasting Details Forecasting Log Transformed Data Specifying Series Periodicity Detecting Outliers OUT= Data Set OUTCOV= Data Set OUTEST= Data Set OUTMODEL= SAS Data Set OUTSTAT= Data Set Printed Output ODS Table Names Statistical Graphics
The Inverse Autocorrelation Function The Partial Autocorrelation Function The Cross-Correlation Function The ESACF Method The MINIC Method The SCAN Method Stationarity Tests Prewhitening Identifying Transfer Function Models Missing Values and Autocorrelations Estimation Details Specifying Inputs and Transfer Functions Initial Values Stationarity and Invertibility Naming of Model Parameters Missing Values and Estimation and Forecasting Forecasting Details Forecasting Log Transformed Data Specifying Series Periodicity Detecting Outliers OUT= Data Set OUTCOV= Data Set OUTEST= Data Set OUTMODEL= SAS Data Set OUTSTAT= Data Set Printed Output ODS Table Names Statistical Graphics
 ' from a gas furnace. (Data values are not shown. The full example including data is in the SAS/ETS sample library.)
' from a gas furnace. (Data values are not shown. The full example including data is in the SAS/ETS sample library.)