| The MODEL Procedure |
Example 18.16 Simulated Method of Moments—AR(1) Process
This example illustrates how to use SMM to estimate an AR(1) regression model for the following process:
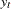 |
 |
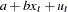 |
|||
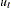 |
 |
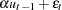 |
|||
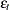 |
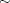 |
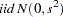 |
In the following SAS statements, 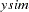 is simulated by using this model, and the endogenous variable
is simulated by using this model, and the endogenous variable  is set to be equal to
is set to be equal to 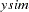 . The MOMENT statement creates two more moments for the estimation. One is the second moment and the other is the first-order autocovariance. The NPREOBS=20 option instructs PROC MODEL to run the simulation 20 times before
. The MOMENT statement creates two more moments for the estimation. One is the second moment and the other is the first-order autocovariance. The NPREOBS=20 option instructs PROC MODEL to run the simulation 20 times before 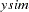 is compared to the first observation of
is compared to the first observation of  . Because the initial
. Because the initial 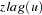 is zero, the first
is zero, the first 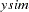 is
is 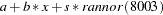 . Without the NPREOBS option, this
. Without the NPREOBS option, this 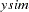 is matched with the first observation of
is matched with the first observation of  . With NPREOBS, this
. With NPREOBS, this 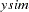 , along with the next 19
, along with the next 19 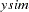 , is thrown away, and the moment match starts with the twenty-first
, is thrown away, and the moment match starts with the twenty-first 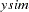 with the first observation of
with the first observation of  . This way, the initial values do not exert a large inference on the simulated endogenous variables.
. This way, the initial values do not exert a large inference on the simulated endogenous variables.
%let nobs=500;
data ardata;
lu =0;
do i=-10 to &nobs;
x = rannor( 1011 );
e = rannor( 1011 );
u = .6 * lu + 1.5 * e;
Y = 2 + 1.5 * x + u;
lu = u;
if i > 0 then output;
end;
run;
title1 'Simulated Method of Moments for AR(1) Process';
proc model data=ardata ;
parms a b s 1 alpha .5;
instrument x;
u = alpha * zlag(u) + s * rannor( 8003 );
ysim = a + b * x + u;
y = ysim;
eq.ysq = y*y - ysim*ysim;
eq.ylagy = y * lag(y) - ysim * lag( ysim );
fit y ysq ylagy / gmm npreobs=10 ndraw=10;
bound s > 0, 1 > alpha > 0;
run;
The output of the MODEL procedure is shown in Output 18.16.1:
| Model Summary | |
|---|---|
| Model Variables | 1 |
| Parameters | 4 |
| Equations | 3 |
| Number of Statements | 6 |
| Program Lag Length | 1 |
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.