PROC MODEL: Simulated Method of Moments—Stochastic Volatility Model

The MODEL Procedure

Example 18.17 Simulated Method of Moments—Stochastic Volatility Model

This example illustrates how to use SMM to estimate a stochastic volatility model as in Andersen and Sorensen (1996):

$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

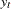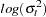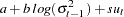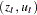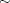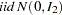This model is widely used in modeling the return process of stock prices and foreign exchange rates. This is called the stochastic volatility model because the volatility is stochastic as the random variable 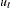$\text{[math]}$ appears in the volatility equation. The following SAS statements use three moments: absolute value, the second-order moment, and absolute value of the first-order autoregressive moment. Note the ADJSMMV option in the FIT statement to request the SMM covariance adjustment for the parameter estimates. Although these moments have closed form solution as shown by Andersen and Sorensen (1996), the simulation approach significantly simplifies the moment conditions.

   %let nobs=1000;
   data _tmpdata;
      a = -0.736; b=0.9; s=0.363;
      ll=sqrt( exp(a/(1-b)));;
      do i=-10 to &nobs;
         u = rannor( 101 );
         z = rannor( 98761 );
         lnssq = a+b*log(ll**2) +s*u;
         st = sqrt(exp(lnssq));
         ll = st;
         y = st * z;
         if i > 0 then output;
      end;
   run;
   
   title1 'Simulated Method of Moments for Stochastic Volatility Model';
   
   proc model data=_tmpdata ;
      parms a b .5 s 1;
      instrument _exog_ / intonly;
   
      u = rannor( 8801 );
      z = rannor( 9701 );
      lsigmasq = xlag(sigmasq,exp(a));
      lnsigmasq = a + b * log(lsigmasq) + s * u;
      sigmasq = exp( lnsigmasq );
   
      ysim = sqrt(sigmasq) * z;
      eq.m1 = abs(y) - abs(ysim);
      eq.m2 = y**2 - ysim**2;
      eq.m5 = abs(y*lag(y))-abs(ysim*lag(ysim));
   
      fit m1 m2 m5 / gmm npreobs=10 ndraw=10;
      bound s > 0, 1 > b > 0;
   run;

The output of the MODEL procedure is shown in Output 18.17.1.

Output 18.17.1 PROC MODEL Output

Simulated Method of Moments for Stochastic Volatility Model

The MODEL Procedure

Model Summary
Parameters	3
Equations	3
Number of Statements	10
Program Lag Length	1

Parameters(Value)	a b(0.5) s(1)
Equations	m1 m2 m5

The 3 Equations to Estimate
m1 =	F(a, b, s)
m2 =	F(a, b, s)
m5 =	F(a, b, s)
Instruments	1

Nonlinear GMM Parameter Estimates
Parameter	Estimate	Approx Std Err	t Value	Approx Pr > \|t\|
a	-2.2299	1.0357	-2.15	0.0316
b	0.695469	0.1417	4.91	<.0001
s	0.747779	0.1491	5.02	<.0001

Top of Page