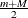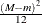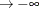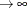The HPQLIM Procedure
Prior Distributions
The PRIOR statement specifies the prior distribution of the model parameters. You must specify one parameter or a list of
parameters, a tilde  , and then a distribution with its parameters. You can specify multiple PRIOR
statements to define independent priors. Parameters that are associated with a regressor variable are referred to by the
name of the corresponding regressor variable.
, and then a distribution with its parameters. You can specify multiple PRIOR
statements to define independent priors. Parameters that are associated with a regressor variable are referred to by the
name of the corresponding regressor variable.
You can specify the special keyword _REGRESSORS to consider all the regressors of a model. If multiple PRIOR statements affect the same parameter, the last PRIOR statement prevails. For example, in a regression with two regressors (X1, X2), the following statements imply that the prior on X1 is NORMAL(MEAN=0, VAR=1), the prior on X2 is GAMMA(SHAPE=3, SCALE=4).
... prior _Regressors ~ uniform(min=0, max=1); prior X1 X2 ~ gamma(shape=3, scale=4); prior X1 ~ normal(mean=0, var=1); ...
If a parameter is not associated with a PRIOR statement or if some of the prior hyperparameters are missing, then the default choices in Table Table 8.3 are considered.
Table 8.3: Default Values for Prior Distributions
|
PRIOR Distribution |
|
|
|
|
|
|---|---|---|---|---|---|
|
NORMAL |
|
|
|
|
|
|
IGAMMA |
|
|
|
|
|
|
GAMMA |
|
|
|
|
|
|
UNIFORM |
|
|
|||
|
BETA |
|
|
|
|
|
|
T |
|
|
|
|
For density specification, see the section Standard Distributions.
Standard Distributions
Table 8.4 through Table 8.9 show all the distribution density functions that PROC HPQLIM recognizes. You specify these distribution densities in the PRIOR statement.
Table 8.4: Beta Distribution
|
PRIOR statement |
BETA(SHAPE1=a, SHAPE2=b, MIN=m, MAX=M) |
|
Note: Commonly |
|
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Defaults |
SHAPE1=SHAPE2=1, |
Table 8.5: Gamma Distribution
|
PRIOR statement |
GAMMA(SHAPE=a, SCALE=b) |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Defaults |
SHAPE=SCALE=1 |
Table 8.6: Inverse Gamma Distribution
|
PRIOR statement |
IGAMMA(SHAPE=a, SCALE=b) |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Defaults |
SHAPE=2.000001, SCALE=1 |
Table 8.7: Normal Distribution
|
PRIOR statement |
NORMAL(MEAN= |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Defaults |
MEAN=0, VAR=1000000 |
Table 8.8: t Distribution
|
PRIOR statement |
T(LOCATION= |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Defaults |
LOCATION=0, DF=3 |
Table 8.9: Uniform Distribution
|
PRIOR statement |
UNIFORM(MIN=m, MAX=M) |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
Not unique |
|
Defaults |
MIN |

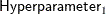
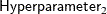
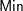
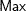
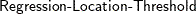
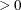
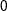
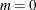
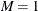
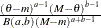
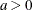
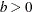
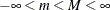
![$ \left\{ \begin{array}{ll} \left[ m, M \right] & \mbox{when } a = 1, b = 1 \\ \left[ m, M \right) & \mbox{when } a = 1, b \neq 1 \\ \left( m, M \right] & \mbox{when } a \neq 1, b = 1 \\ \left( m, M \right) & \mbox{otherwise} \end{array} \right. $](images/etshpug_hpqlim0144.png)
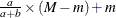
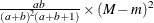
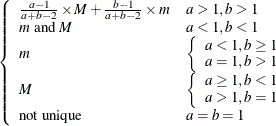
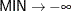
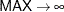
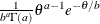
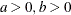
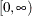
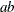
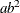
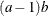
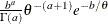
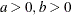
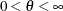

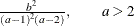
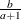
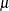
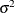
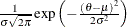
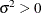
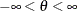

![$\frac{\Gamma \left(\frac{\nu +1}{2}\right)}{\Gamma \left(\frac{\nu }{2}\right)\sqrt {\pi \nu }}\left[1+\frac{(\theta -\mu )^2}{\nu }\right]^{-\frac{\nu +1}{2}} $](images/etshpug_hpqlim0165.png)
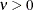
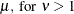
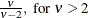
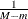
![$ \theta \in [m, M]$](images/etshpug_hpqlim0170.png)