The HPQLIM Procedure

Limited Dependent Variable Models

Subsections:

Censored Regression Models

When the dependent variable is censored, values in a certain range are all transformed to a single value. For example, the standard Tobit model can be defined as

\[ y^{*}_{i} = \mathbf{x}_{i}’\bbeta + \epsilon _{i} \]
\[ y_{i} = \left\{ \begin{array}{ll} y^{*}_{i} & \mr{if} y^{*}_{i}>0 \\ 0 & \mr{if} y^{*}_{i}\leq 0 \end{array} \right. \]

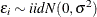where $\epsilon _{i} \sim iid N(0,\sigma ^{2})$.

The Tobit model can be generalized to handle observation-by-observation censoring. The censored model on both the lower and upper limits can be defined as

\[ y_{i} = \left\{ \begin{array}{ll} R_{i} & \mr{if} \; y_{i}^{*} \geq R_{i} \\ y_{i}^{*} & \mr{if} \; L_{i} < y_{i}^{*} < R_{i} \\ L_{i} & \mr{if} \; y_{i}^{*} \leq L_{i} \end{array} \right. \]

You can see Censored Regression Models: Censored Regression Models in SAS/ETS 14.1 User's Guide, for more details.

Truncated Regression Models

In a truncated model, the observed sample is a subset of the population where the dependent variable falls within a certain range. For example, when neither a dependent variable nor exogenous variables are observed for 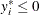$y^{*}_{i} \leq 0$, the truncated regression model can be specified as

\[ \ell = \sum _{i\in \{ y_{i}>0\} } \left\{ -\ln \Phi (\mathbf{x}_{i}’\bbeta /\sigma ) + \ln \left[\frac{\phi ((y_{i} - \mathbf{x}_{i}'\bbeta )/\sigma )}{\sigma } \right] \right\} \]

For more information, see the section Truncated Regression Models in SAS/ETS 14.1 User's Guide.