The HPQLIM Procedure

Bayesian Analysis

Subsections:

To perform Bayesian analysis, you must specify a BAYES statement. Unless otherwise stated, all options that are described in this section are options in the BAYES statement.

By default, PROC HPQLIM uses the random walk Metropolis algorithm to obtain posterior samples. For the implementation details of the Metropolis algorithm in PROC HPQLIM, such as the blocking of the parameters and tuning of the covariance matrices, see the sections Blocking of Parameters and Tuning the Proposal Distribution.

The Bayes theorem states that

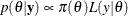
\begin{equation*} p(\theta | \mb{y})\propto \pi (\theta ) L(y|\theta ) \end{equation*}

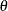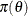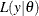where $\theta $ is a parameter or a vector of parameters and $\pi (\theta )$ is the product of the prior densities that are specified in the PRIOR statement. The term $L(y|\theta )$ is the likelihood that is associated with the MODEL statement.

Blocking of Parameters

In a multivariate parameter model, all the parameters are updated in one single block (by default or when you specify the SAMPLING=MULTIMETROPOLIS option). This can be inefficient, especially when parameters have vastly different scales. As an alternative, you can update the parameters one at a time (by specifying SAMPLING=UNIMETROPOLIS).

Tuning the Proposal Distribution

One key factor in achieving high efficiency of a Metropolis-based Markov chain is finding a good proposal distribution for each block of parameters. This process is called tuning. The tuning phase consists of a number of loops that are controlled by the options MINTUNE and MAXTUNE. The MINTUNE= option controls the minimum number of tuning loops and has a default value of 2. The MAXTUNE= option controls the maximum number of tuning loops and has a default value of 24. Each loop repeats the number of times specified by the NTU= option, which has a default of 500. At the end of every loop, PROC HPQLIM examines the acceptance probability for each block. The acceptance probability is the percentage of NTU proposed values that have been accepted. If this probability does not fall within the acceptance tolerance range (see the following section), the proposal distribution is modified before the next tuning loop.

A good proposal distribution should resemble the actual posterior distribution of the parameters. Large sample theory states that the posterior distribution of the parameters approaches a multivariate normal distribution (Gelman et al. 2004, Appendix B; Schervish 1995, Section 7.4). That is why a normal proposal distribution often works well in practice. The default proposal distribution in PROC HPQLIM is the normal distribution.

You can see Bayesian Analysis: Bayesian Analysis in SAS/ETS 14.1 User's Guide, for more details.

Initial Values of the Markov Chains

You can assign initial values to any parameters. For more information, see the INIT statement. If you use the optimization PROPCOV= option, PROC HPQLIM starts the tuning at the optimized values. This option overwrites the provided initial values.