The HPSEVERITY Procedure

PROC HPSEVERITY Statement

PROC HPSEVERITY options;

The PROC HPSEVERITY statement invokes the procedure. You can specify two types of options in the PROC HPSEVERITY statement. One set of options controls input and output. The other set of options controls the model estimation and selection process.

The following options control the input data sets used by PROC HPSEVERITY and various forms of output generated by PROC HPSEVERITY. The options are listed in alphabetical order.

COVOUT

specifies that the OUTEST= data set contain the estimate of the covariance structure of the parameters. This option has no effect if you do not specify the OUTEST= option. For more information about how the covariance is reported in the OUTEST= data set, see the section OUTEST= Data Set.

DATA=SAS-data-set

names the input data set. If you do not specify the DATA= option, then the most recently created SAS data set is used.

EDFALPHA=confidence-level

specifies the confidence level in the (0,1) range that is used for computing the confidence intervals for the EDF estimates. The lower and upper confidence limits that correspond to this level are reported in the OUTCDF= data set, if specified, and are displayed in the plot that is created when you specify the PLOTS=CDFPERDIST option.

If you do not specify the EDFALPHA= option, then PROC HPSEVERITY uses a default value of 0.05.

INEST=SAS-data-set

names the input data set that contains the initial values of the parameter estimates to start the optimization process. The initial values that you specify in the INIT= option in the DIST statement take precedence over any initial values that you specify in the INEST= data set. For more information about the variables in this data set, see the section INEST= Data Set.

If you specify the SCALEMODEL statement, then PROC HPSEVERITY reads the INEST= data set only if the SCALEMODEL statement contains singleton continuous effects. For more generic regression effects, you should save the estimates by specifying the OUTSTORE= item store in a step and then use the INSTORE= option to read those estimates. The INSTORE= option is the newer and more flexible method of specifying initial values for distribution and regression parameters.

INITSAMPLE (initsample-option) INITSAMPLE (initsample-option …initsample-option)

specifies that a sample of the input data be used for initializing the distribution parameters. If you specify more than one initsample-option, then separate them with spaces.

When you do not specify initial values for the distribution parameters, PROC HPSEVERITY needs to compute the empirical distribution function (EDF) estimates as part of the default method for parameter initialization. The EDF estimation process can be expensive, especially when you specify censoring or truncation effects for the loss variable. Furthermore, it is not amenable to parallelism due to the sequential nature of the algorithm for truncation effects. You can use the INITSAMPLE option to specify that only a fraction of the input data be used in order to reduce the time taken to compute the EDF estimates. PROC HPSEVERITY uses the uniform random sampling method to select the sample, the size and randomness of which is controlled by the following initsample-options:

FRACTION=number: specifies the fraction, between 0 and 1, of the input data to be used for sampling.
SEED=number: specifies the seed to be used for the uniform random number generator. This option enables you to select the same sample from the same input data across different runs of PROC HPSEVERITY, which can be useful for replicating the results across different runs. If you do not specify the seed value, PROC HPSEVERITY generates a seed that is based on the system clock.
SIZE=number: specifies the size of the sample. If the data are distributed across different nodes, then this size applies to the sample that is prepared at each node. For example, let the input data set of size 100,000 observations be distributed across 10 nodes such that each node has 10,000 observations. If you specify SIZE=1000, then each node computes a local EDF estimate by using a sample of size 1,000 selected randomly from its 10,000 observations. If you specify both of the SIZE= and FRACTION= options, then the value that you specify in the SIZE= option is used and the FRACTION= option is ignored.

If you do not specify the INITSAMPLE option, then a uniform random sample of at most 10,000 observations is used for EDF estimation.

INSTORE=store-name

names the item store that contains the context and results of the severity model estimation process. An item store has a binary file format that cannot be modified. You must specify an item store that you have created in another PROC HPSEVERITY step by using the OUTSTORE= option.

The store-name is a usual one- or two-level SAS name, as for SAS data sets. If you specify a one-level name, then PROC HPSEVERITY reads the item store from the WORK library. If you specify a two-level name of the form libname.membername, then PROC HPSEVERITY reads the item store from the libname library.

This option is more flexible than the INEST= option, because it can read estimates of any type of scale regression model; the INEST= option can read only scale regression models that contain singleton continuous effects.

For more information about how the input item store is used for parameter initialization, see the sections Parameter Initialization and Parameter Initialization for Regression Models.

NAMELEN=number

specifies the length to which long regression effect names are shortened. The default and minimum value is 20.

This option does not apply to the names of singleton continuous effects if you have not specified any CLASS variables.

NOCLPRINT<=number>

suppresses the display of the "Class Level Information" table if you do not specify number. If you specify number, the values of the classification variables are displayed for only those variables whose number of levels is less than number. Specifying a number helps to reduce the size of the "Class Level Information" table if some classification variables have a large number of levels. This option has no effect if you do not specify the CLASS statement.

NOPRINT

turns off all displayed and graphical output. If you specify this option, then any value that you specify for the PRINT= and PLOTS= options is ignored.

OUTCDF=SAS-data-set

names the output data set to contain estimates of the cumulative distribution function (CDF) value at each of the observations. This data set is created only when you run PROC HPSEVERITY in single-machine mode.

The information is output for each specified model whose parameter estimation process converges. The data set also contains the estimates of the empirical distribution function (EDF). For more information about the variables in this data set, see the section OUTCDF= Data Set.

OUTEST=SAS-data-set

names the output data set to contain estimates of the parameter values and their standard errors for each model whose parameter estimation process converges. For more information about the variables in this data set, see the section OUTEST= Data Set.

If you specify the SCALEMODEL statement such that it contains at least one effect that is not a singleton continuous effect, then the OUTEST= data set that this option creates cannot be used as an INEST= data set in a subsequent PROC HPSEVERITY step. In such cases, it is recommended that you use the newer OUTSTORE= option to save the estimates and specify those estimates in a subsequent PROC HPSEVERITY step by using the INSTORE= option.

OUTMODELINFO=SAS-data-set

names the output data set to contain the information about each candidate distribution. For more information about the variables in this data set, see the section OUTMODELINFO= Data Set.

OUTSTAT=SAS-data-set

names the output data set to contain the values of statistics of fit for each model whose parameter estimation process converges. For more information about the variables in this data set, see the section OUTSTAT= Data Set.

OUTSTORE=store-name

names the item store to contain the context and results of the severity model estimation process. The resulting item store has a binary file format that cannot be modified. You can specify this item store in a subsequent PROC HPSEVERITY step by using the INSTORE= option.

The store-name is a usual one- or two-level SAS name, as for SAS data sets. If you specify a one-level name, then the item store resides in the WORK library and is deleted at the end of the SAS session. Because item stores are meant to be consumed by a subsequent PROC HPSEVERITY step for parameter initialization, typical usage specifies a two-level name of the form libname.membername.

This option is more useful than the OUTEST= option, especially when you specify a scale regression model that contains interaction effects or effects that have CLASS variables. You can initialize such scale regression models in a subsequent PROC HPSEVERITY step only by specifying the item store that this option creates as an INSTORE= item store in that step.

PLOTS <(global-plot-options)> <=plot-request-option> PLOTS <(global-plot-options)> <=(plot-request-option …plot-request-option)>

specifies the desired graphical output. The graphical output is created only when you run PROC HPSEVERITY in single-machine mode. If you specify more than one global-plot-option, then separate them with spaces and enclose them in parentheses. If you specify more than one plot-request-option, then separate them with spaces and enclose them in parentheses.

You can specify the following global-plot-options:

HISTOGRAM: plots the histogram of the response variable on the PDF plots.
KERNEL: plots the kernel estimate of the probability density of the response variable on the PDF plots.
ONLY: turns off the default graphical output and creates only the requested plots.

You can specify the following plot-request-options:

ALL: creates all the graphical output.
CDF: creates a plot that compares the cumulative distribution function (CDF) estimates of all the candidate distribution models to the empirical distribution function (EDF) estimate. The plot does not contain CDF estimates for models whose parameter estimation process does not converge.
CDFPERDIST: creates a plot of the CDF estimates of each candidate distribution model. A plot is not created for models whose parameter estimation process does not converge.
NONE: creates none of the graphical output. If you specify this option, then it overrides all the other plot-request-options. The default graphical output is also suppressed.
PDF: creates a plot that compares the probability density function (PDF) estimates of all the candidate distribution models. The plot does not contain PDF estimates for models whose parameter estimation process does not converge.
PDFPERDIST: creates a plot of the PDF estimates of each candidate distribution model. A plot is not created for models whose parameter estimation process does not converge.
PP: creates the probability-probability plot (known as the P-P plot), which compares the CDF estimate of each candidate distribution model to the empirical distribution function (EDF). The data that are shown in this plot are used for computing the EDF-based statistics of fit.
QQ: creates the quantile-quantile plot (known as the Q-Q plot), which compares the empirical quantiles to the quantiles of each candidate distribution model.

If you do not specify the PLOTS= option or if you do not specify the ONLY global-plot-option, then the default graphical output is equivalent to specifying PLOTS(HISTOGRAM KERNEL)=(CDF PDF).

PRINT <(global-display-option)> <=display-option> PRINT <(global-display-option)> <= (display-option …display-option) >

specifies the desired displayed output. If you specify more than one display-option, then separate them with spaces and enclose them in parentheses.

You can specify the following global-display-option:

ONLY: turns off the default displayed output and displays only the requested output.

You can specify the following display-options:

ALL: displays all the output.
ALLFITSTATS: displays the comparison of all the statistics of fit for all the models in one table. The table does not include the models whose parameter estimation process does not converge.
CONVSTATUS: displays the convergence status of the parameter estimation process.
DESCSTATS: displays the descriptive statistics for the response variable. If you specify the SCALEMODEL statement, then this option also displays the descriptive statistics for the regression effects that do not contain a CLASS variable.
DISTINFO: displays the information about each specified distribution. For each distribution, the information includes the name, description, validity status, and number of distribution parameters.
ESTIMATES | PARMEST: displays the final estimates of parameters. The estimates are not displayed for models whose parameter estimation process does not converge.
ESTIMATIONDETAILS: displays the details of the estimation process for all the models in one table.
INITIALVALUES: displays the initial values and bounds used for estimating each model.
NLOHISTORY: displays the iteration history of the nonlinear optimization process used for estimating the parameters.
NLOSUMMARY: displays the summary of the nonlinear optimization process used for estimating the parameters.
NONE: displays none of the output. If you specify this option, then it overrides all other display options. The default displayed output is also suppressed.
SELECTION | SELECT: displays the model selection table.
STATISTICS | FITSTATS: displays the statistics of fit for each model. The statistics of fit are not displayed for models whose parameter estimation process does not converge.

If you do not specify the PRINT= option or if you do not specify the ONLY global-display-option, then the default displayed output is equivalent to specifying PRINT=(SELECTION CONVSTATUS NLOSUMMARY STATISTICS ESTIMATES).

VARDEF=DF | N

specifies the denominator to use for computing the covariance estimates. You can specify one of the following values:

DF: specifies that the number of nonmissing observations minus the model degrees of freedom (number of parameters) be used.
N: specifies that the number of nonmissing observations be used.

For more information about the covariance estimation, see the section Estimating Covariance and Standard Errors.

The following options control the model estimation and selection process:

CRITERION | CRITERIA | CRIT=criterion-option

specifies the model selection criterion.

If you specify two or more candidate models for estimation, then the one with the best value for the selection criterion is chosen as the best model. If you specify the OUTSTAT= data set, then the best model’s observation has a value of 1 for the _SELECTED_ variable.

You can specify one of the following criterion-options:

AD

specifies the Anderson-Darling (AD) statistic value, which is computed by using the empirical distribution function (EDF) estimate, as the selection criterion. A lower value is deemed better.

AIC

specifies Akaike’s information criterion (AIC) as the selection criterion. A lower value is deemed better.

AICC

specifies the finite-sample corrected Akaike’s information criterion (AICC) as the selection criterion. A lower value is deemed better.

BIC

specifies the Schwarz Bayesian information criterion (BIC) as the selection criterion. A lower value is deemed better.

CUSTOM

specifies the custom objective function as the selection criterion. You can specify this only if you also specify the OBJECTIVE= option. A lower value is deemed better.

CVM

specifies the Cra

$\'{m}$

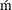
er-von Mises (CvM) statistic value, which is computed by using the empirical distribution function (EDF) estimate, as the selection criterion. A lower value is deemed better.

KS

specifies the Kolmogorov-Smirnov (KS) statistic value, which is computed by using the empirical distribution function (EDF) estimate, as the selection criterion. A lower value is deemed better.

LOGLIKELIHOOD | LL

specifies 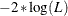$-2 * \log (L)$ as the selection criterion, where L is the likelihood of the data. A lower value is deemed better. This is the default.

For more information about these criterion-options, see the section Statistics of Fit.

EMPIRICALCDF | EDF=method

specifies the method to use for computing the nonparametric or empirical estimate of the cumulative distribution function of the data. You can specify one of the following values for method:

AUTOMATIC | AUTO

specifies that the method be chosen automatically based on the data specification.

If you do not specify any censoring or truncation, then the standard empirical estimation method (STANDARD) is chosen. If you specify both right-censoring and left-censoring, then Turnbull’s estimation method (TURNBULL) is chosen. For all other combinations of censoring and truncation, the Kaplan-Meier method (KAPLANMEIER) is chosen.

KAPLANMEIER | KM

specifies that the product limit estimator proposed by Kaplan and Meier (1958) be used. Specification of this method has no effect when you specify both right-censoring and left-censoring.

MODIFIEDKM | MKM <(options)>

specifies that the modified product limit estimator be used. Specification of this method has no effect when you specify both right-censoring and left-censoring.

This method allows Kaplan-Meier’s product limit estimates to be more robust by ignoring the contributions to the estimate due to small risk-set sizes. The risk set is the set of observations at the risk of failing, where an observation is said to fail if it has not been processed yet and might experience censoring or truncation. You can specify the minimum risk-set size that makes it eligible to be included in the estimation either as an absolute lower bound on the size (RSLB= option) or a relative lower bound determined by the formula 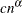$c n^{\alpha }$ proposed by Lai and Ying (1991). You can specify the values of c and $\alpha$ by using the C= and ALPHA= options, respectively. By default, the relative lower bound is used with values of c = 1 and $\alpha$ = 0.5. However, you can modify the default by using the following options:

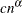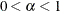ALPHA | A=number: specifies the value to use for $\alpha$ when the lower bound on the risk set size is defined as $c n^{\alpha }$ . This value must satisfy $0 < \alpha < 1$ .
C=number: specifies the value to use for c when the lower bound on the risk set size is defined as 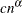$c n^{\alpha }$ . This value must satisfy $c > 0$ .
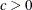RSLB=number: specifies the absolute lower bound on the risk set size to be included in the estimate.

NOTURNBULL

specifies that the method be chosen automatically based on the data specification and that Turnbull’s method not be used. This option is the default.

This method first replaces each left-censored or interval-censored observation with an uncensored observation. If the resulting set of observations has any truncated or right-censored observations, then the Kaplan-Meier method (KAPLANMEIER) is chosen. Otherwise, the standard empirical estimation method (STANDARD) is chosen. The observations are modified only for the purpose of computing the EDF estimates; the modification does not affect the parameter estimation process.

STANDARD | STD

specifies that the standard empirical estimation method be used. If you specify both right-censoring and left-censoring, then the specification of this method has no effect. If you specify any other combination of censoring or truncation effects, then this method ignores such effects, and can thus result in estimates that are more biased than those obtained with other methods that are more suitable for censored or truncated data.

TURNBULL | EM <(options)>

specifies that the Turnbull’s method be used. This method is used when you specify both right-censoring and left-censoring. An iterative expectation-maximization (EM) algorithm proposed by Turnbull (1976) is used to compute the empirical estimates. If you also specify truncation, then the modification suggested by Frydman (1994) is used.

This method is used if you specify both right-censoring and left-censoring and if you explicitly specify the EMPIRICALCDF=TURNBULL option.

You can modify the default behavior of the EM algorithm by using the following options:

ENSUREMLE: specifies that the final EDF estimates be maximum likelihood estimates. The Kuhn-Tucker conditions are computed for the likelihood maximization problem and checked to ensure that EM algorithm converges to maximum likelihood estimates. The method generalizes the method proposed by Gentleman and Geyer (1994) by taking into account any truncation information that you might specify.
EPS=number: specifies the maximum relative error to be allowed between estimates of two consecutive iterations. This criterion is used to check the convergence of the algorithm. If you do not specify this option, then PROC HPSEVERITY uses a default value of 1.0E–8.
MAXITER=number: specifies the maximum number of iterations to attempt to find the empirical estimates. If you do not specify this option, then PROC HPSEVERITY uses a default value of 500.
ZEROPROB=number: specifies the threshold below which an empirical estimate of the probability is considered zero. This option is used to decide if the final estimate is a maximum likelihood estimate. This option does not have an effect if you do not specify the ENSUREMLE option. If you specify the ENSUREMLE option, but do not specify this option, then PROC HPSEVERITY uses a default value of 1.0E–8.

For more information about each of the methods, see the section Empirical Distribution Function Estimation Methods.

OBJECTIVE=symbol-name

names the symbol that represents the objective function in the SAS programming statements that you specify. For each model to be estimated, PROC HPSEVERITY executes the programming statements to compute the value of this symbol for each observation. The values are added across all observations to obtain the value of the objective function. The optimization algorithm estimates the model parameters such that the objective function value is minimized. A separate optimization problem is solved for each candidate distribution. If you specify a BY statement, then a separate optimization problem is solved for each candidate distribution within each BY group.

For more information about writing SAS programming statements to define your own objective function, see the section Custom Objective Functions.