The HPQLIM Procedure
This example shows the use of the Bayesian analysis available in the HPQLIM procedure with an emphasis on processing a large data set and on the performance improvements that are achieved by executing in a high-performance distributed environment.
The model and the data set are the same as in Example 4.1, and the priors are set to the defaults.
The model is executed in the distributed computing environment with two threads and only one node. These settings are used to obtain a hypothetical environment that might resemble running the HPQLIM procedure on a desktop workstation with a dual-core CPU. To run the following statements successfully, you need to set the macro variables GRIDHOST and GRIDINSTALLLOC to resolve to appropriate values, or you can replace the references to the macro variables in the example with the appropriate values.
option set=GRIDHOST="&GRIDHOST";
option set=GRIDINSTALLLOC="&GRIDINSTALLLOC";
proc hpqlim data=simulate ;
bayes nbi=10000 nmc=30000;
performance nthreads=2 nodes=1 details ;
model y=x1-x7 /censored(lb=0 ub=400);
run;
Output 4.2.1 shows a summary of the posterior distribution that is associated with the censored model when you use diffuse prior distributions.
Output 4.2.1: Posterior Summary for Bayesian Censored Model
| Estimating a Tobit model |
| Posterior Summaries | ||||||
|---|---|---|---|---|---|---|
| Parameter | N | Mean | Standard Deviation |
Percentiles | ||
| 25% | 50% | 75% | ||||
| Intercept | 30000 | 2.2104 | 0.2219 | 2.0605 | 2.2115 | 2.3629 |
| x1 | 30000 | 3.0565 | 0.1991 | 2.9205 | 3.0585 | 3.1925 |
| x2 | 30000 | 4.0045 | 0.1992 | 3.8706 | 4.0054 | 4.1342 |
| x3 | 30000 | 1.8466 | 0.1993 | 1.7142 | 1.8502 | 1.9823 |
| x4 | 30000 | 4.1695 | 0.1965 | 4.0355 | 4.1700 | 4.3059 |
| x5 | 30000 | -3.0167 | 0.1983 | -3.1511 | -3.0167 | -2.8843 |
| x6 | 30000 | -5.1583 | 0.1895 | -5.2845 | -5.1611 | -5.0255 |
| x7 | 30000 | -2.6868 | 0.2038 | -2.8267 | -2.6860 | -2.5529 |
| _Sigma | 30000 | 400.0 | 0.2597 | 399.8 | 400.0 | 400.2 |
Output 4.2.2 show a summary of the performance when you use a distributed computing environment with one node and two threads.
Output 4.2.2: Performance Analysis for Bayesian Censored Model on One Node with Two Threads
| Estimating a Tobit model |
| Performance Information | |
|---|---|
| Host Node | << your grid host >> |
| Execution Mode | Distributed |
| Grid Mode | Symmetric |
| Number of Compute Nodes | 1 |
| Number of Threads per Node | 2 |
| Estimating a Tobit model |
| Procedure Task Timing | ||
|---|---|---|
| Task | Seconds | Percent |
| Reading and Levelizing Data | 3.73 | 0.00% |
| Communication to Client | 0.15 | 0.00% |
| Bayesian Analysis: Likelihood for MCMC | 86759.60 | 99.85% |
| Bayesian Analysis: MCMC | 1.15 | 0.00% |
| Optimization | 124.95 | 0.14% |
| Post-optimization | 0.00 | 0.00% |
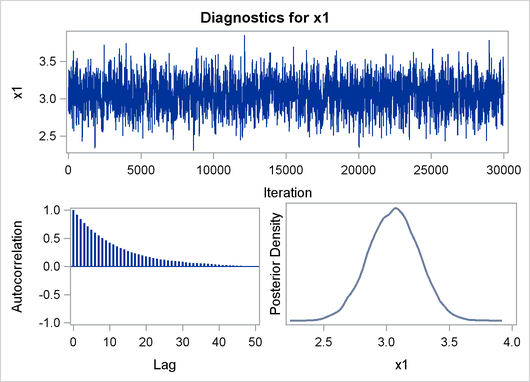
Finally, Output 4.2.3 shows the diagnostic and summary plots that are associated with X1.
In the following statements, the PERFORMANCE statement is modified to use a grid with 10 nodes, where each node spawns eight threads:
option set=GRIDHOST="&GRIDHOST";
option set=GRIDINSTALLLOC="&GRIDINSTALLLOC";
proc hpqlim data=simulate ;
bayes nbi=10000 nmc=30000;
performance nthreads=8 nodes=10 details ;
model y=x1-x7 /censored(lb=0 ub=400);
run;
The two models are identical, but the second implementation, which was run on a grid that used 10 nodes with eight threads each, took only 49 minutes instead of 24 hours and 6 minutes to sample from the same posterior distribution.
Output 4.2.4: Performance Analysis for Bayesian Censored Model on Ten Nodes with Eight Threads Each
| Estimating a Tobit model |
| Performance Information | |
|---|---|
| Host Node | << your grid host >> |
| Execution Mode | Distributed |
| Grid Mode | Symmetric |
| Number of Compute Nodes | 10 |
| Number of Threads per Node | 8 |
| Estimating a Tobit model |
| Procedure Task Timing | ||
|---|---|---|
| Task | Seconds | Percent |
| Reading and Levelizing Data | 0.31 | 0.01% |
| Communication to Client | 0.17 | 0.01% |
| Bayesian Analysis: Likelihood for MCMC | 2921.57 | 99.85% |
| Bayesian Analysis: MCMC | 0.55 | 0.02% |
| Optimization | 3.43 | 0.12% |
| Post-optimization | 0.00 | 0.00% |