The HPQLIM Procedure

Tests on Parameters

In general, the tested hypothesis can be written as

$H_{0}: \mb {h} (\theta ) = 0$

where ${\mb {h} (\theta )}$ is an r $\times$ 1 vector-valued function of the parameters ${\theta }$ given by the r expressions that are specified in the TEST statement.

Let ${\hat{V}}$ be the estimate of the covariance matrix of ${\hat{\theta }}$ . Let ${\hat{\theta }}$ be the unconstrained estimate of ${\theta }$ and ${\tilde{\theta }}$ be the constrained estimate of ${\theta }$ such that ${h(\tilde{\theta }) = 0}$ . Let

$A(\theta ) = {{\partial } h(\theta )}/{{\partial } \theta }~ |_{\hat{\theta }}$

Using this notation, the test statistics for the three types of tests are computed as follows.

The Wald test statistic is defined as

$W = h^{}(\hat{\theta })\big \lgroup { {A(\hat{\theta }) \hat{V} A^{} (\hat{\theta })} }\big \rgroup ^{-1} h(\hat{\theta })$

The Wald test is not invariant to reparameterization of the model (Gregory and Veall 1985; Gallant 1987, p. 219). For more information about the theoretical properties of the Wald test, see Phillips and Park (1988).
The Lagrange multiplier test statistic is

$LM = {\lambda }^{} A(\tilde{\theta }) \tilde{V} A^{}(\tilde{\theta }) {\lambda }$

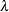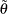where ${{\lambda }}$ is the vector of Lagrange multipliers from the computation of the restricted estimate ${\tilde{\theta }}$ .
The likelihood ratio test statistic is

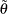$LR = 2 \left({L(\hat{\theta }) - L(\tilde{\theta })}\right)$

where ${\tilde{\theta }}$ represents the constrained estimate of 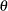${\theta }$ and 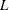is the concentrated log-likelihood value.

For each type of test, under the null hypothesis the test statistic is asymptotically distributed as a ${{\chi }^{2}}$ random variable with r degrees of freedom, where r is the number of expressions in the TEST statement. The p-values reported for the tests are computed from the ${{\chi }^{2}(r)}$ distribution and are only asymptotically valid.

Monte Carlo simulations suggest that the asymptotic distribution of the Wald test is a poorer approximation to its small sample distribution than that of the other two tests. However, the Wald test has the lowest computational cost, because it does not require computation of the constrained estimate ${\tilde{\theta }}$ .

The following statements use the TEST statement to perform a likelihood ratio test:

   proc hpqlim;
      model y = x1 x2 x3;
      test x1 = 0, x2 * .5 + 2 * x3 = 0 /lr;
   run;