The VARCOMP Procedure
Example 121.2 Using the GRR Method
In this example from Houf and Burman (1988), the response variable is the thermal performance of a module measured in Celsius degrees per watt. Each of three operators measures 10 parts three times. It is assumed that parts and operators are selected at random from larger populations. The following statements produce Output 121.2.1.
data Houf; input a b y @@; datalines; 1 1 37 1 1 38 1 1 37 1 2 41 1 2 41 1 2 40 1 3 41 1 3 42 1 3 41 2 1 42 2 1 41 2 1 43 2 2 42 2 2 42 2 2 42 2 3 43 2 3 42 2 3 43 3 1 30 3 1 31 3 1 31 3 2 31 3 2 31 3 2 31 3 3 29 3 3 30 3 3 28 4 1 42 4 1 43 4 1 42 4 2 43 4 2 43 4 2 43 4 3 42 4 3 42 4 3 42 5 1 28 5 1 30 5 1 29 5 2 29 5 2 30 5 2 29 5 3 31 5 3 29 5 3 29 6 1 42 6 1 42 6 1 43 6 2 45 6 2 45 6 2 45 6 3 44 6 3 46 6 3 45 7 1 25 7 1 26 7 1 27 7 2 28 7 2 28 7 2 30 7 3 29 7 3 27 7 3 27 8 1 40 8 1 40 8 1 40 8 2 43 8 2 42 8 2 42 8 3 43 8 3 43 8 3 41 9 1 25 9 1 25 9 1 25 9 2 27 9 2 29 9 2 28 9 3 26 9 3 26 9 3 26 10 1 35 10 1 34 10 1 34 10 2 35 10 2 35 10 2 34 10 3 35 10 3 34 10 3 35 ;
proc varcomp data=Houf method=grr (speclimits=(18,58) ratio); class a b; model y=a|b/cl; run;
You specify METHOD= GRR in this example to drive the VARCOMP procedure to produce a gauge repeatability and reproducibility analysis . With the option speclimits=(18 58), the parameters PTR and Cp are estimated and displayed. With the RATIO option, certain additional ratios of variance components are also estimated and displayed. Finally, the CL= option in the MODEL statement specifies that estimates of GRR quantities should have the corresponding confidence limits.
Output 121.2.1: Class Level Information Using Method=GRR
The "Class Level Information" table in Output 121.2.1 displays the levels of each variable specified in the CLASS statement.
Output 121.2.2: Analysis of Variance Using Method=GRR
| GRR Analysis of Variance | ||||
|---|---|---|---|---|
| Source | DF | Sum of Squares | Mean Square | Expected Mean Square |
| a | 9 | 3935.955556 | 437.328395 | Var(Error) + 3 Var(a*b) + 9 Var(a) |
| b | 2 | 39.266667 | 19.633333 | Var(Error) + 3 Var(a*b) + 30 Var(b) |
| a*b | 18 | 48.511111 | 2.695062 | Var(Error) + 3 Var(a*b) |
| Error | 60 | 30.666667 | 0.511111 | Var(Error) |
| Corrected Total | 89 | 4054.400000 | ||
The GRR analysis of variance in Output 121.2.2 is the same as for the Type I analysis when the design is balanced.
Finally, the estimates of the GRR parameters of interest and their confidence limits are displayed in Output 121.2.3.
Output 121.2.3: Parameter Estimates Using Method=GRR
| GRR Estimates | |||
|---|---|---|---|
| Parameter | Estimate | 95% Confidence Limits | |
| Mu Y | 35.80000 | 30.49477 | 41.10523 |
| Var(a) | 48.29259 | 22.69452 | 161.63918 |
| Var(b) | 0.56461 | 0.07296 | 25.75077 |
| Var(a*b) | 0.72798 | 0.33273 | 1.79272 |
| Var(Error) | 0.51111 | 0.36816 | 0.75754 |
| Gamma Y | 50.09630 | 24.48844 | 166.22217 |
| Gamma P | 48.29259 | 22.69452 | 161.63918 |
| Gamma M | 1.80370 | 1.20623 | 27.01724 |
| Gamma R | 26.77413 | 1.69168 | 105.60895 |
| SNR | 7.31767 | 1.83939 | 14.53334 |
| PTR(18,58,6) | 0.20145 | 0.16474 | 0.77967 |
| Cp(18,58,6) | 0.95933 | 0.52437 | 1.39942 |
| DR | 54.54825 | 4.38336 | 212.21791 |
| Rho P | 0.96400 | 0.62848 | 0.99062 |
| Rho M | 0.03600 | 0.0093801 | 0.37152 |
| Var(a)/Gamma Y | 0.96400 | 0.62848 | 0.99062 |
| Var(b)/Gamma Y | 0.01127 | 0.0008700 | 0.34151 |
| Var(a*b)/Gamma Y | 0.01453 | 0.0027083 | 0.04744 |
| Var(a)/Var(Error) | 94.48551 | 40.19199 | 327.32469 |
| Var(b)/Var(Error) | 1.10467 | 0.13662 | 50.37744 |
| Var(a*b)/Var(Error) | 1.42432 | 0.55232 | 3.74691 |
You can draw the following inferences from the results of the analysis. Most of the variation is due to differences between parts because of the relative larger value of Gamma R . The measurement system is nearly inadequate because the PTR exceeds 20%. However, the measurement system is of value in monitoring the process since the SNR is greater than five. See Burdick, Borror, and Montgomery (2003) for more information about interpreting gauge R&R studies.
The confidence limits in Output 121.2.3 are based on large-sample asymptotic approximation. You can alternatively compute more accurate and usually smaller confidence intervals by using CL=GCL for generalized confidence limits. The following statements produce Output 121.2.4:
proc varcomp data=Houf method=grr (speclimits=(18,58) ratio) seed=104; class a b; model y=a|b/cl=gcl; run;
Output 121.2.4: Generalized Confidence Limits
| GRR Estimates | |||
|---|---|---|---|
| Parameter | Estimate | 95% Generalized Confidence Limits |
|
| Mu Y | 35.80000 | 30.23607 | 41.39887 |
| Var(a) | 48.29259 | 22.46186 | 160.90542 |
| Var(b) | 0.56461 | 0.06936 | 29.93347 |
| Var(a*b) | 0.72798 | 0.33182 | 1.79558 |
| Var(Error) | 0.51111 | 0.36816 | 0.75754 |
| Gamma Y | 50.09630 | 25.20454 | 175.29591 |
| Gamma P | 48.29259 | 22.46186 | 160.90542 |
| Gamma M | 1.80370 | 1.18137 | 31.03229 |
| Gamma R | 26.77413 | 1.66841 | 84.92030 |
| SNR | 7.31767 | 1.82670 | 13.03229 |
| PTR(18,58,6) | 0.20145 | 0.16304 | 0.83560 |
| Cp(18,58,6) | 0.95933 | 0.52556 | 1.40665 |
| DR | 54.54825 | 4.33682 | 170.84061 |
| Rho P | 0.96400 | 0.62524 | 0.98836 |
| Rho M | 0.03600 | 0.01164 | 0.37476 |
| Var(a)/Gamma Y | 0.96400 | 0.62524 | 0.98836 |
| Var(b)/Gamma Y | 0.01127 | 0.0009352 | 0.35629 |
| Var(a*b)/Gamma Y | 0.01453 | 0.0032977 | 0.04258 |
| Var(a)/Var(Error) | 94.48551 | 40.62919 | 325.51792 |
| Var(b)/Var(Error) | 1.10467 | 0.13051 | 56.94205 |
| Var(a*b)/Var(Error) | 1.42432 | 0.55232 | 3.74691 |
Note that the generalized confidence interval widths from Output 121.2.4 for parameters 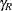 and DR are 85.7 and 171.4, respectively. These widths are much shorter than the MLS-based widths, which are 103.9 and 207.8
from Output 121.2.3.
and DR are 85.7 and 171.4, respectively. These widths are much shorter than the MLS-based widths, which are 103.9 and 207.8
from Output 121.2.3.
In general, the GCL method provides a more accurate confidence interval with a shorter interval width than the MLS method. However, as discussed in the section Generalized Confidence Limits, they are computationally intensive and somewhat nondeterministic, because they are based on an underlying Monte Carlo simulation.
