The SURVEYFREQ Procedure

Kappa Coefficients

Simple Kappa Coefficient

The KAPPA option provides an estimate of the simple kappa coefficient, its standard error, and the confidence limits. This option is available with replication-based variance estimation methods (which you can request by specifying the VARMETHOD=JACKKNIFE or VARMETHOD=BRR option).

The simple kappa coefficient (Cohen 1960) is a measure of interrater agreement, where the row and column variables of the two-way table are viewed as two independent ratings. When there is perfect agreement between the two ratings, the kappa coefficient is +1. When the observed agreement exceeds chance agreement, the value of kappa is positive, and its magnitude reflects the strength of agreement. The minimum value of kappa is between –1 and 0, depending on the marginal proportions. For more information, see Fleiss, Levin, and Paik (2003).

PROC SURVEYFREQ computes the simple kappa coefficient as

\[ \hat{\kappa } = \left( P_ o - P_ e \right) ~ / ~ \left( 1-P_ e \right) \]

where

\[ P_ o = \sum _ i \widehat{P}_{ii} \]
\[ P_ e = \sum _ i \left( \widehat{P}_{i \cdot } \widehat{P}_{\cdot i} \right) \]

where $\widehat{P}_{ii}$ is the estimate of the proportion in table cell (i, i), $\widehat{P}_{i \cdot }$ is the estimate of the proportion in row i, and $\widehat{P}_{\cdot i}$ is the estimate of the proportion in column i. For information about how PROC SURVEYFREQ computes the proportion estimates, see the section Proportions.

If you request jackknife variance estimation (by specifying the VARMETHOD=JACKKNIFE option), PROC SURVEYFREQ estimates the variance of the simple kappa coefficient as described in the section The Jackknife Method. If you request BRR variance estimation (by specifying the VARMETHOD=BRR option in the PROC SURVEYFREQ statement), the procedure estimates the variance as described in the section Balanced Repeated Replication (BRR).

PROC SURVEYFREQ computes confidence limits for the simple kappa coefficient as

\[ \hat{\kappa } \pm \left( t_{\mi{df}, \alpha /2} \times \mr{StdErr}(\hat{\kappa }) \right) \]

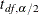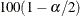where $\mr{StdErr}(\hat{\kappa })$ is the standard error of the kappa coefficient and $t_{\mi{df}, \alpha /2}$ is the $100(1-\alpha /2)$th percentile of the t distribution with df degrees of freedom. (For more information, see the section Degrees of Freedom.) The value of the confidence coefficient $\alpha $ is determined by the ALPHA= option; by default, ALPHA=0.05, which produces 95% confidence limits.

Weighted Kappa Coefficient

The weighted kappa coefficient is a generalization of the simple kappa coefficient that uses agreement weights to quantify the relative difference between categories (levels). By default, PROC SURVEYFREQ uses Cicchetti-Allison agreement weights to compute the weighted kappa coefficient; if you specify the WTKAPPA(WT=FC) option, the procedure uses Fleiss-Cohen agreement weights. For information about how the agreement weights are computed, see the section Kappa Agreement Weights. For more information, see Fleiss, Cohen, and Everitt (1969) and Fleiss, Levin, and Paik (2003).

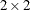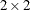For $2 \times 2$ tables, the weighted kappa coefficient equals the simple kappa coefficient; PROC SURVEYFREQ displays the weighted kappa coefficient only for tables larger than $2 \times 2$.

PROC SURVEYFREQ computes the weighted kappa coefficient as

\[ \hat{\kappa }_ w = \left( P_{o(w)} - P_{e(w)} \right) ~ / ~ \left( 1-P_{e(w)} \right) \]

where

\[ P_{o(w)} = \sum _ i \sum _ j \left( w_{ij} \widehat{P}_{ij} \right) \]
\[ P_{e(w)} = \sum _ i \sum _ j \left( w_{ij} \widehat{P}_{i \cdot } \widehat{P}_{\cdot j} \right) \]

where $w_{ij}$ is the agreement weight for table cell (i, j), $\widehat{P}_{ij}$ is the estimate of the proportion in table cell (i, j), $\widehat{P}_{i \cdot }$ is the estimate of the proportion in row i, and $\widehat{P}_{\cdot i}$ is the estimate of the proportion in column i. For information about how PROC SURVEYFREQ computes the proportion estimates, see the section Proportions.

If you request jackknife variance estimation (by specifying the VARMETHOD=JACKKNIFE option), PROC SURVEYFREQ estimates the variance of the weighted kappa coefficient as described in the section The Jackknife Method. If you request BRR variance estimation (by specifying the VARMETHOD=BRR option in the PROC SURVEYFREQ statement), the procedure estimates the variance as described in the section Balanced Repeated Replication (BRR).

PROC SURVEYFREQ computes confidence limits for the weighted kappa coefficient as

\[ \hat{\kappa }_ w \pm \left( t_{\mi{df}, \alpha /2} \times \mr{StdErr}(\hat{\kappa }_ w) \right) \]

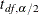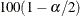where $\mr{StdErr}(\hat{\kappa }_ w)$ is the standard error of the weighted kappa coefficient and $t_{\mi{df}, \alpha /2}$ is the $100(1-\alpha /2)$th percentile of the t distribution with df degrees of freedom. (For more information, see the section Degrees of Freedom.) The value of the confidence coefficient $\alpha $ is determined by the ALPHA= option; by default, ALPHA=0.05, which produces 95% confidence limits.

Kappa Agreement Weights

PROC SURVEYFREQ computes the weighted kappa coefficient by using the Cicchetti-Allison form (by default) or the Fleiss-Cohen form of agreement weights. These weights are based on the scores of the column variable in the two-way table request. If the column variable is numeric, the column scores are the numeric values of the column levels. If the column variable is a character variable, the column scores are the column numbers, where the columns are numbered in the order in which they appear in the crosstabulation table.

PROC SURVEYFREQ computes Cicchetti-Allison agreement weights as

\[ w_{ij} = 1 - \left( |C_ i - C_ j| ~ / ~ (C_ c - C_1) \right) \]

where $C_ i$ is the score for column i and c is the number of columns (categories). For more information, see Cicchetti and Allison (1971).

PROC SURVEYFREQ computes Fleiss-Cohen agreement weights as

\[ w_{ij} = 1 - \left( (C_ i - C_ j) ~ / ~ (C_ c - C_1) \right)^2 \]

For more information, see Fleiss and Cohen (1973).

The agreement weights $w_{ij}$ are constructed so that $w_{ii}=1$ for all i, and $w_{ij}=w_{ji}$. For $i\not=j$, the agreement weights must be nonnegative and less than 1, which is always true for character variables (where the scores are the column numbers). For numeric variables, you should assign numeric variable levels (scores) so that all agreement weights are nonnegative and less than 1.

You can assign numeric values to the variable levels in a way that reflects their degree of similarity. For example, suppose the column variable is numeric and has four levels, which you order according to similarity. If you assign the values 0, 2, 4, and 10 to the column variable levels, the Cicchetti-Allison agreement weights take the following values: $ w_{12}$ = 0.8, $ w_{13}$ = 0.6, $ w_{14}$ = 0.0, $ w_{23}$ = 0.8, $ w_{24}$ = 0.2, and $ w_{34}$ = 0.4. For this example, the Fleiss-Cohen agreement weights are as follows: $ w_{12}$ = 0.96, $ w_{13}$ = 0.84, $ w_{14}$ = 0.00, $ w_{23}$ = 0.96, $ w_{24}$ = 0.36, and $ w_{34}$ = 0.64.

To display the kappa agreement weights, you can specify the WTKAPPA(PRINTKWTS) option.