The SURVEYFREQ Procedure
Proportions
PROC SURVEYFREQ computes the estimate of the proportion in table cell (r, c) as the ratio of the estimated total for the table cell to the estimated overall total,
![\begin{eqnarray*} \widehat{P}_{rc} & = & \widehat{N}_{rc} ~ / ~ \widehat{N} \\[0.1in]& = & \left( \sum _{h=1}^ H ~ \sum _{i=1}^{n_ h} ~ \sum _{j=1}^{m_{hi}} ~ {\delta _{hij} (r,c) ~ W_{hij}} \right) ~ / ~ \left( \sum _{h=1}^ H ~ \sum _{i=1}^{n_ h} ~ \sum _{j=1}^{m_{hi}} ~ {W_{hij}} \right) \end{eqnarray*}](images/statug_surveyfreq0046.png)
If you request BRR variance estimation (by specifying the VARMETHOD=BRR option in the PROC SURVEYFREQ statement), the procedure estimates the variances of proportion estimates as described in the section Balanced Repeated Replication (BRR). If you request jackknife variance estimation (by specifying the VARMETHOD=JACKKNIFE option), the procedure estimates the variances as described in the section The Jackknife Method.
If you do not specify the VARMETHOD= option or a REPWEIGHTS statement, the default variance estimation method is Taylor series, which you can also request by specifying the VARMETHOD=TAYLOR option. By using Taylor series linearization, the variance of a proportion estimate can be expressed as
![\[ \widehat{\mr{Var}}(\widehat{P}_{rc}) = \sum _{h=1}^ H \widehat{\mr{Var}}_ h(\widehat{P}_{rc}) \]](images/statug_surveyfreq0047.png)
where if 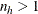 ,
,
![\begin{eqnarray*} \widehat{\mr{Var}}_ h(\widehat{P}_{rc}) & =& \frac{n_ h(1-f_ h)}{n_ h-1} ~ \sum _{i=1}^{n_ h} (e_{rc}^{~ hi} - \bar{e}_{rc}^{~ h})^2 \\ e_{rc}^{~ hi} & =& \left( \sum _{j=1}^{m_{hi}} ~ ({\delta _{hij} (r,c) - \widehat{P}_{rc}) ~ W_{hij}} \right) ~ / ~ \widehat{N} \\[0.1in] \bar{e}_{rc}^{~ h} & =& \left( \sum _{i=1}^{n_ h} ~ {e_{rc}^{~ hi}} \right) ~ / ~ n_ h \end{eqnarray*}](images/statug_surveyfreq0048.png)
and if 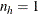 ,
,
![\[ \widehat{\mr{Var}}_ h(\widehat{P}_{rc}) = \left\{ \begin{array}{ll} \mbox{missing} & \mbox{ if } n_{h'}=1 \mbox{ for } h’=1, 2, \ldots , H \\ 0 & \mbox{ if } n_{h'}>1 \mbox{ for some } 1 \leq h’ \leq H \end{array} \right. \]](images/statug_surveyfreq0049.png)
The standard error of the proportion is computed as
![\[ \mr{StdErr}( \widehat{P}_{rc} ) = \sqrt { \widehat{\mr{Var}}( \widehat{P}_{rc} ) } \]](images/statug_surveyfreq0050.png)
Similarly, the estimate of the proportion in row r is
![\[ \widehat{P}_{r \cdot } = \widehat{N}_{r \cdot } ~ / ~ \widehat{N} \]](images/statug_surveyfreq0051.png)
And its variance estimate is
![\[ \widehat{\mr{Var}}(\widehat{P}_{r \cdot }) = \sum _{h=1}^ H \widehat{\mr{Var}}_ h(\widehat{P}_{r \cdot }) \]](images/statug_surveyfreq0052.png)
where if 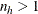 ,
,
![\begin{eqnarray*} \widehat{\mr{Var}}_ h(\widehat{P}_{r \cdot }) & =& \frac{n_ h(1-f_ h)}{n_ h-1} ~ \sum _{i=1}^{n_ h} (e_{r \cdot }^{~ hi} - \bar{e}_{r \cdot }^{~ h})^2 \\ e_{r \cdot }^{ hi} & =& \left( \sum _{j=1}^{m_{hi}} ({\delta _{hij} (r ~ \cdot ) - \widehat{P}_{r \cdot }) ~ W_{hij}} \right) ~ / ~ \widehat{N} \\[0.1in] \bar{e}_{r \cdot }^{ h} & =& \left( \sum _{i=1}^{n_ h} ~ {e_{r \cdot }^{~ hi}} \right) ~ / ~ n_ h \end{eqnarray*}](images/statug_surveyfreq0053.png)
and if 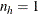 ,
,
![\[ \widehat{\mr{Var}}_ h(\widehat{P}_{r \cdot }) = \left\{ \begin{array}{ll} \mbox{missing} & \mbox{ if } n_{h'}=1 \mbox{ for } h’=1, 2, \ldots , H \\ 0 & \mbox{ if } n_{h'}>1 \mbox{ for some } 1 \leq h’ \leq H \end{array} \right. \]](images/statug_surveyfreq0054.png)
The standard error of the proportion in row r is computed as
![\[ \mr{StdErr}( \widehat{P}_{r \cdot } ) = \sqrt { \widehat{\mr{Var}}( \widehat{P}_{r \cdot } ) } \]](images/statug_surveyfreq0055.png)
Computations for the proportion in column c are done in the same way.
