The QUANTSELECT Procedure
Quantile Process Regression
You can specify QUANTILE=PROCESS in the MODEL statement to perform quantile process regression. Quantile process regression fits quantile regression models for the entire range of quantile levels from 0 to 1. Because a quantile function is the inverse of its cumulative distribution function, quantile process regression can estimate the entire distribution of a response variable conditional on its covariates.
Because of the piecewise linearity of the check loss function, the optimal quantile regression solution 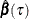 is a step function in
is a step function in ![$\tau \in [0,1]$](images/statug_qrsel0075.png) . In other words, given any optimal solution
. In other words, given any optimal solution 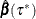 , there exists an optimal quantile-level range
, there exists an optimal quantile-level range ![$[\tau _1,\tau _2]$](images/statug_qrsel0077.png) such that
such that 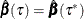 is optimal for any
is optimal for any ![$\tau \in [\tau _1,\tau _2]$](images/statug_qrsel0079.png) . This step-function property can simplify integration computation in quantile process regression. For example, to estimate
conditional mean by using quantile process regression, you can substitute integration by using the summation
. This step-function property can simplify integration computation in quantile process regression. For example, to estimate
conditional mean by using quantile process regression, you can substitute integration by using the summation
![\[ E(Y|\bX =\mb{x})=\int _0^1\mb{x}\hat{\bbeta }(\tau )d\tau =\mb{x}\sum _{i=1}^ s (\tau _{i+1}-\tau _ i)\hat{\bbeta }_ i \]](images/statug_qrsel0080.png)
where 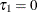 ,
, 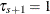 , and
, and 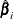 is the optimal solution for quantile range
is the optimal solution for quantile range ![$[\tau _ i,\tau _{i+1}]$](images/statug_qrsel0084.png) .
.
If you specify the NTAU=ALL suboption in the QUANTILE=PROCESS option, PROC QUANTSELECT outputs 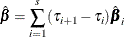 as the mean parameter estimates in the parameter estimates table. If you request the "Parameter Estimates for Quantile Process"
table, PROC QUANTSELECT outputs parameter estimates in the following quantile-level grid:
as the mean parameter estimates in the parameter estimates table. If you request the "Parameter Estimates for Quantile Process"
table, PROC QUANTSELECT outputs parameter estimates in the following quantile-level grid:
![\[ \left\{ 0,{\tau _1+\tau _2\over 2},{\tau _2+\tau _3\over 2},\ldots ,{\tau _ s+\tau _{s+1}\over 2},1\right\} \]](images/statug_qrsel0086.png)
For more information about the "Parameter Estimates for Quantile Process" table, see Parameter Estimates for Quantile Process. PROC QUANTSELECT also uses this grid to estimate observation quantile levels.
If you specify NTAU=n, PROC QUANTSELECT approximates the quantile process regression in the following quantile-level grid:
![\[ \left\{ 0,{1\over n+1},{2\over n+1},\ldots ,0.5,\ldots ,{n\over n+1},1\right\} \]](images/statug_qrsel0087.png)
When NTAU=n, PROC QUANTSELECT also approximates integrations by using the linear interpolation method, which defines
![\[ \hat{\bbeta }(\tau )={\tau -\tau _1\over \tau _2-\tau _1}\hat{\bbeta }(\tau _2)+{\tau _2-\tau \over \tau _2-\tau _1}\hat{\bbeta }(\tau _1) \]](images/statug_qrsel0088.png)
Here,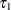 and
and 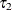 denote two consecutive quantile levels in the quantile-level grid that satisfy
denote two consecutive quantile levels in the quantile-level grid that satisfy ![$\tau \in [\tau _1,\tau _2]$](images/statug_qrsel0079.png) .
.
