The PHREG Procedure

Type 3 Tests and Joint Tests

Subsections:

For models that use less-than-full-rank parameterization (as specified by the PARAM=GLM option in the CLASS statement), a Type 3 test of an effect of interest (main effect or interaction) is a test of the Type III estimable functions that are defined for that effect. When the model contains no missing cells, the Type 3 test of a main effect corresponds to testing the hypothesis of equal marginal means. For more information about Type III estimable functions, see Chapter 46: The GLM Procedure, and Chapter 15: The Four Types of Estimable Functions. Also see Littell, Freund, and Spector (1991).

For models that use full-rank parameterization, all parameters are estimable when there are no missing cells, so it is unnecessary to define estimable functions. The standard test of an effect of interest in this case is the joint test that the values of the parameters associated with that effect are zero. For a model that uses effects parameterization (as specified by the PARAM=EFFECT option in the CLASS statement), the joint test for a main effect is equivalent to testing the equality of marginal means. For a model that uses reference parameterization (as specified by the PARAM=REF option in the CLASS statement), the joint test is equivalent to testing the equality of cell means at the reference level of the other model effects. For more information about the coding scheme and the associated interpretation of results, see Muller and Fetterman (2002, Chapter 14).

If there is no interaction term, the Type 3 test of an effect for a model that uses GLM parameterization is the same as the joint test of the effect for the model that uses full-rank parameterization. In this situation, the joint test is also called the Type 3 test. For a model that contains an interaction term and no missing cells, the Type 3 test of a component main effect under GLM parameterization is the same as the joint test of the component main effect under effect parameterization. Both test the equality of cell means. But this Type 3 test differs from the joint test under reference parameterization, which tests the equality of cell means at the reference level of the other component main effect. If some cells are missing, you can obtain meaningful tests only by testing a Type III estimation function, so in this case you should use GLM parameterization.

The results of a Type 3 test or a joint test do not depend on the order in which you specify the terms in the MODEL statement.

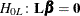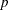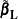The following statistics can be used to test the null hypothesis $H_{0L}\colon {\mb{L}\bbeta } = \Strong{0}$, where $\mb{L}$ is a matrix of known coefficients. Under mild assumptions, each of the following statistics has an asymptotic chi-square distribution with $\mi{p}$ degrees of freedom, where p is the rank of $\mb{L}$. Let $\tilde{\bbeta }_{\mb{L}}$ be the maximum likelihood of 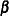$\bbeta $ under the null hypothesis 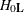$H_{0\mb{L}}$; that is,

\[ l(\tilde{\bbeta }_{\mb{L}}) = \max _{\mb{L}\bbeta =0}l(\bbeta ) \]

Likelihood Ratio Statistic

\[ \chi ^{2}_{\mr{LR}}=2 \left[ l (\hat{\bbeta }) - l(\tilde{\bbeta }_{\mb{L}}) \right] \]

Score Statistic

\[ \chi ^{2}_{S}= \left[\frac{ \partial l(\tilde{\bbeta }_{\mb{L}}) }{ \partial {\bbeta } } \right]’ \left[-\frac{\partial ^2 l(\tilde{\bbeta }_{\mb{L}})}{\partial \bbeta ^2} \right]^{-1} \left[ \frac{ \partial l(\tilde{\bbeta }_{\mb{L}}) }{ \partial {\bbeta } } \right] \]

Wald’s Statistic

\[ \chi ^{2}_{W}=\left( \mb{L}\hat{\bbeta } \right) ’ \left[ \mb{L}\hat{\mb{V}}(\hat{\bbeta })\mb{L}’ \right] ^{-1} \left( \mb{L}\hat{\bbeta } \right) \]

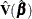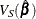where $\hat{\bV }(\hat{\bbeta })$ is the estimated covariance matrix, which can be the model-based covariance matrix $\left[-\frac{\partial ^2 l(\hat{\bbeta })}{\partial \bbeta ^2} \right]^{-1}$ or the sandwich covariance matrix $V_ S(\hat{\bbeta })$. For more information, see the section Robust Sandwich Variance Estimate.