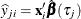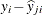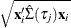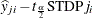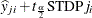The HPQUANTSELECT Procedure

Diagnostic Statistics

This section gathers the formulas for the statistics available in the OUTPUT statement. All the statistics available in the OUTPUT statement are conditional on the selected model and do not take into account the variability that is introduced by doing model selection.

The model to be fit is 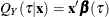$Q_ Y(\tau |\mb{x})=\mb{x}’\bbeta (\tau )$, and the parameter estimate 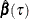$\hat{\bbeta }(\tau )$ is the solution that minimizes 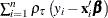$\sum _{i=1}^ n \rho _\tau \left(y_ i-\mb{x}_ i^{\prime }\bbeta \right)$. The subscript i is for the ith observation. The subscript j is for the jth-smallest quantile level among all the specified QUANTILE= levels in the MODEL statement. 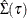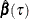$\hat{\Sigma }(\tau )$ denotes the covariance estimation for $\hat{\bbeta }(\tau )$.

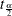The ALPHA= option in the PROC HPQUANTSELECT statement sets the $\alpha $ value for the confidence limit statistics. The degrees of freedom for $t_{\frac{\alpha }{2}}$ are $n-p$.

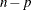Table 59.7 contains the diagnostic statistics and their formulas. Each statistic is computed for each observation.

Table 59.7: Formulas and Definitions for Diagnostic Statistics

MODEL Option or Statistic

Formula

PREDj

$\widehat{y}_{ji}=\mb{x}_ i’\hat{\bbeta }(\tau _ j)$

RESj

$y_ i - \widehat{y}_{ji}$

STDPj

$\sqrt {\mb{x}_ i’\hat{\Sigma }(\tau _ j)\mb{x}_ i}$

LCLMj

$\widehat{y}_{ji}-t_{\frac{\alpha }{2}}\mbox{STDP}j_{i}$

UCLMj

$\widehat{y}_{ji}+t_{\frac{\alpha }{2}}\mbox{STDP}j_{i}$