The HPGENSELECT Procedure

RESTRICT Statement

RESTRICT <’label’> constraint-specification <, …, constraint-specification><operator <value>> </ option>;

The RESTRICT statement enables you to specify linear equality or inequality constraints among the parameters of a model. These restrictions are incorporated into the maximum likelihood analysis.

Following are reasons why you might want to place constraints and restrictions on the model parameters:

to fix a parameter at a particular value
to equate parameters in a model
to impose order conditions on the parameters in a model
to specify contrasts among the parameters that the fitted model should honor

A restriction is composed of a left-hand side and a right-hand side, separated by an operator. If you do not specify the operator and right-hand side, the restriction is assumed to be an equality constraint against zero. If you do not specify the right-hand side, the value is assumed to be zero.

You write an individual constraint-specification in (nearly) the same form as you specify estimable linear functions in the ESTIMATE statement of the GLM, MIXED, or GLIMMIX procedure. The constraint-specification takes the form

model-effect value-list < …model-effect value-list >

You must specify at least one model-effect, followed by one or more values in the value-list. The values in the list correspond to the multipliers of the corresponding parameter that is associated with the position in the model effect. If you specify more values in the value-list than the model-effect occupies in the model design matrix, the extra coefficients are ignored.

The following statements provide an example. Here, A is a CLASS variable that has three levels.

proc hpgenselect;
   class A;
   model y/n = A x /  dist=binomial;
   restrict A 1 0 -1;
   restrict x 2 >= 0.5;
run;

The linear predictor for this model can be written as

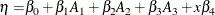
$\begin{align*} \eta =& \beta _{0} + \beta _{1}A_1 + \beta _{2}A_2 + \beta _{3}A_3+ x\beta _{4} \\ \end{align*}$

where 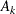$A_ k$ is the binary variable associated with the kth level of A.

The first RESTRICT statement specifies that the parameter estimates that are associated with the first and third levels of the A effect be identical. In terms of the linear predictor, the restriction can be written as

$\beta _{1} - \beta _{3} = 0$

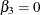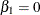Because, in the default GLM parameterization, $\beta _3=0$ , the RESTRICT statement has the effect of setting $\beta _1=0$ .

The second RESTRICT statement involves the regression parameter associated with the variable x and specifies that the parameter estimate satisfy 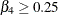$\beta _4\geq 0.25$ . In terms of the linear predictor, the restriction can be written as

$2 \beta _{4} \geq \frac{1}{2}$

PROC HPGENSELECT applies both of these restrictions when it computes the maximum likelihood estimates of the regression parameters of the model.

Zero-inflated models contain two components: a model for the mean of the underlying distribution and a model for the zero-inflation probability. To specify restrictions for effects in specific components of the model, separate the constraint-specifications by commas. The following statements provide an example:

proc hpgenselect data=b itdetails itselect cov;
   class  C;
   model B = C / dist=ZIP;
   zeromodel X;
   restrict Intercept 0, X 1 = 0;
run;

In this example, the model for the mean has a single regressor, which is specified by the CLASS variable C. The model for the zero-inflation probability has a continuous regressor X. The RESTRICT statement specifies that the parameter estimate associated with X be constrained to be 0. The Intercept 0 constraint-specification serves as a placeholder and has no effect on the model for the mean. You must include this model-effect value-list pair in order to specify constraints on the zero-inflation part of the model. You can use any model-effect in the model for the mean in place of Intercept. For example, the following statement has the same effect, because C is in the model for the mean:

   restrict C 0, X 1 = 0;

The generalized logit model for a nominal multinomial response consists of a regression model for each nonreference level of the response variable. To specify restrictions for effects in specific components of the model, you specify a constraint-specification for each component to which you want to apply constraints. You specify the constraint-specifications in the sort order of the response variable and separate them with commas. You must specify a null constraint-specification with a value-list set to zero for each component model that has a lower response variable sort order than the one to which you want to apply constraints. The following statements provide an example. In this example, a generalized logit regression model is fit to the categorical response variable Y, with four levels. The generalized logit model consists of a regression model with a CLASS regressor Visit and a continuous regressor Lage for each level of the response variable Y. The RESTRICT statements constrain the model to have identical values of the estimated regression coefficient for Lage for all three nonreference categories of Y; that is, a common-slopes model is fit. In the second RESTRICT statement, the constraint-specification of Lage 0 is necessary as a placeholder and does not affect the regression coefficient of Lage for the first level of Y.

proc hpgenselect data=thallMult_hgen7809;
   class Visit / Param=Ref;
   model Y=Visit Lage/dist=Multinomial link=Glogit;
   restrict Lage 1 , Lage -1;
   restrict Lage 0 , Lage  1, Lage -1;
run;

You can use following operators to separate the left- and right-hand sides of the restriction: =, >, <, >=, <=.

Some distributions involve a dispersion parameter (the parameter $\phi$ in the expressions for the log likelihood), and in the case of the Tweedie distribution, a power parameter. You cannot use the RESTRICT statement to constrain either of these parameters. Instead, you can use the MODEL statement options PHI= to set the dispersion to a fixed value and P= to set the Tweedie power parameter to a fixed value.

You can specify the following option after a slash (/):

DIVISOR=value: specifies a value by which all coefficients on the right-hand and left-hand sides of the restriction are divided.