The PHREG Procedure
- Overview
-
Getting Started

-
Syntax
 PROC PHREG StatementASSESS StatementBASELINE StatementBAYES StatementBY StatementCLASS StatementCONTRAST StatementEFFECT StatementESTIMATE StatementFREQ StatementHAZARDRATIO StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsRANDOM StatementSTRATA StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement
PROC PHREG StatementASSESS StatementBASELINE StatementBAYES StatementBY StatementCLASS StatementCONTRAST StatementEFFECT StatementESTIMATE StatementFREQ StatementHAZARDRATIO StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsRANDOM StatementSTRATA StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement -
Details
 Failure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelCounting Process Style of InputLeft-Truncation of Failure TimesThe Multiplicative Hazards ModelThe Frailty ModelHazard RatiosProportional Rates/Means Models for Recurrent EventsNewton-Raphson MethodFirth’s Modification for Maximum Likelihood EstimationRobust Sandwich Variance EstimateTesting the Global Null HypothesisType 3 TestsConfidence Limits for a Hazard RatioUsing the TEST Statement to Test Linear HypothesesAnalysis of Multivariate Failure Time DataModel Fit StatisticsResidualsDiagnostics Based on Weighted ResidualsInfluence of Observations on Overall Fit of the ModelSurvivor Function EstimatorsEffect Selection MethodsAssessment of the Proportional Hazards ModelThe Penalized Partial Likelihood Approach for Fitting Frailty ModelsSpecifics for Bayesian AnalysisComputational ResourcesInput and Output Data SetsDisplayed OutputODS Table NamesODS Graphics
Failure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelCounting Process Style of InputLeft-Truncation of Failure TimesThe Multiplicative Hazards ModelThe Frailty ModelHazard RatiosProportional Rates/Means Models for Recurrent EventsNewton-Raphson MethodFirth’s Modification for Maximum Likelihood EstimationRobust Sandwich Variance EstimateTesting the Global Null HypothesisType 3 TestsConfidence Limits for a Hazard RatioUsing the TEST Statement to Test Linear HypothesesAnalysis of Multivariate Failure Time DataModel Fit StatisticsResidualsDiagnostics Based on Weighted ResidualsInfluence of Observations on Overall Fit of the ModelSurvivor Function EstimatorsEffect Selection MethodsAssessment of the Proportional Hazards ModelThe Penalized Partial Likelihood Approach for Fitting Frailty ModelsSpecifics for Bayesian AnalysisComputational ResourcesInput and Output Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise RegressionBest Subset SelectionModeling with Categorical PredictorsFirth’s Correction for Monotone LikelihoodConditional Logistic Regression for m:n MatchingModel Using Time-Dependent Explanatory VariablesTime-Dependent Repeated Measurements of a CovariateSurvival CurvesAnalysis of ResidualsAnalysis of Recurrent Events DataAnalysis of Clustered DataModel Assessment Using Cumulative Sums of Martingale ResidualsBayesian Analysis of the Cox ModelBayesian Analysis of Piecewise Exponential Model
Stepwise RegressionBest Subset SelectionModeling with Categorical PredictorsFirth’s Correction for Monotone LikelihoodConditional Logistic Regression for m:n MatchingModel Using Time-Dependent Explanatory VariablesTime-Dependent Repeated Measurements of a CovariateSurvival CurvesAnalysis of ResidualsAnalysis of Recurrent Events DataAnalysis of Clustered DataModel Assessment Using Cumulative Sums of Martingale ResidualsBayesian Analysis of the Cox ModelBayesian Analysis of Piecewise Exponential Model - References
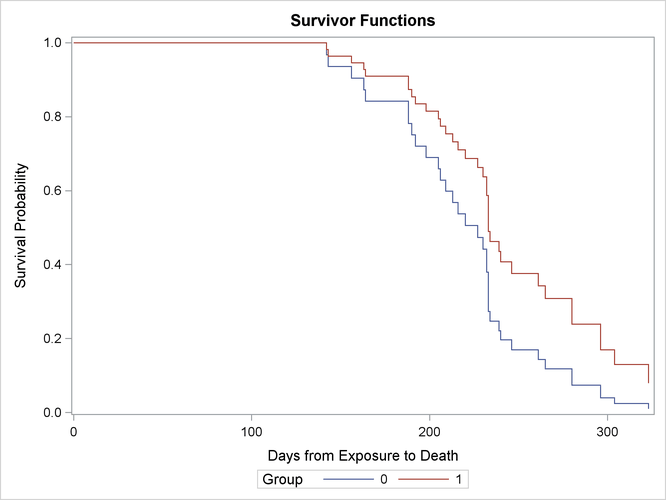
PROC PHREG fits the Cox model by maximizing the partial likelihood and computes the baseline survivor function by using the Breslow (1972) estimate. The following statements produce Figure 67.1 and Figure 67.2:
ods graphics on; proc phreg data=Rats plot(overlay)=survival; model Days*Status(0)=Group; baseline covariates=regimes out=_null_; run; ods graphics off;
In the MODEL statement, the response variable, Days, is crossed with the censoring variable, Status, with the value that indicates censoring is enclosed in parentheses. The values of Days are considered censored if the value of Status is 0; otherwise, they are considered event times.
Graphs are produced when ODS Graphics is enabled. The survival curves for the two observations in the data set Regime, specified in the COVARIATES= option in the BASELINE statement, are requested through the PLOTS= option with the OVERLAY
option for overlaying both survival curves in the same plot.
Figure 67.2 shows a typical printed output of a classical analysis. Since Group takes only two values, the null hypothesis for no difference between the two groups is identical to the null hypothesis that
the regression coefficient for Group is 0. All three tests in the “Testing Global Null Hypothesis: BETA=0” table (see the section Testing the Global Null Hypothesis) suggest that the survival curves for the two pretreatment groups might not be the same. In this model, the hazard ratio (or risk ratio) for Group, defined as the exponentiation of the regression coefficient for Group, is the ratio of the hazard functions between the two groups. The estimate is 0.551, implying that the hazard function for Group=1 is smaller than that for Group=0. In other words, rats in Group=1 lived longer than those in Group=0. This conclusion is also revealed in the plot of the survivor functions in Figure 67.2.
Figure 67.1: Comparison of Two Survival Curves
| Model Information | ||
|---|---|---|
| Data Set | WORK.RATS | |
| Dependent Variable | Days | Days from Exposure to Death |
| Censoring Variable | Status | |
| Censoring Value(s) | 0 | |
| Ties Handling | BRESLOW | |
|
|
|---|
| Summary of the Number of Event and Censored Values |
|||
|---|---|---|---|
| Total | Event | Censored | Percent Censored |
| 40 | 36 | 4 | 10.00 |
| Convergence Status |
|---|
| Convergence criterion (GCONV=1E-8) satisfied. |
| Model Fit Statistics | ||
|---|---|---|
| Criterion | Without Covariates |
With Covariates |
| -2 LOG L | 204.317 | 201.438 |
| AIC | 204.317 | 203.438 |
| SBC | 204.317 | 205.022 |
| Testing Global Null Hypothesis: BETA=0 | |||
|---|---|---|---|
| Test | Chi-Square | DF | Pr > ChiSq |
| Likelihood Ratio | 2.8784 | 1 | 0.0898 |
| Score | 3.0001 | 1 | 0.0833 |
| Wald | 2.9254 | 1 | 0.0872 |
| Analysis of Maximum Likelihood Estimates | ||||||
|---|---|---|---|---|---|---|
| Parameter | DF | Parameter Estimate |
Standard Error |
Chi-Square | Pr > ChiSq | Hazard Ratio |
| Group | 1 | -0.59590 | 0.34840 | 2.9254 | 0.0872 | 0.551 |
In this example, the comparison of two survival curves is put in the form of a proportional hazards model. This approach is essentially the same as the log-rank (Mantel-Haenszel) test. In fact, if there are no ties in the survival times, the likelihood score test in the Cox regression analysis is identical to the log-rank test. The advantage of the Cox regression approach is the ability to adjust for the other variables by including them in the model. For example, the present model could be expanded by including a variable that contains the initial body weights of the rats.
Next, consider a simple test of the validity of the proportional hazards assumption. The proportional hazards model for comparing the two pretreatment groups is given by the following:
The ratio of hazards is ![]() , which does not depend on time. If the hazard ratio changes with time, the proportional hazards model assumption is invalid.
Simple forms of departure from the proportional hazards model can be investigated with the following time-dependent explanatory
variable
, which does not depend on time. If the hazard ratio changes with time, the proportional hazards model assumption is invalid.
Simple forms of departure from the proportional hazards model can be investigated with the following time-dependent explanatory
variable ![]() :
:
Here, ![]() is used instead of t to avoid numerical instability in the computation. The constant, 5.4, is the average of the logs of the survival times and
is included to improve interpretability. The hazard ratio in the two groups then becomes
is used instead of t to avoid numerical instability in the computation. The constant, 5.4, is the average of the logs of the survival times and
is included to improve interpretability. The hazard ratio in the two groups then becomes ![]() , where
, where ![]() is the regression parameter for the time-dependent variable x. The term
is the regression parameter for the time-dependent variable x. The term ![]() represents the hazard ratio at the geometric mean of the survival times. A nonzero value of
represents the hazard ratio at the geometric mean of the survival times. A nonzero value of ![]() would imply an increasing
would imply an increasing ![]() or decreasing
or decreasing ![]() trend in the hazard ratio with time.
trend in the hazard ratio with time.
The following statements implement this simple test of the proportional hazards assumption. The MODEL statement includes the
time-dependent explanatory variable X, which is defined subsequently by the programming statement. At each event time, subjects in the risk set (those alive just before the event time) have their X values changed accordingly.
proc phreg data=Rats; model Days*Status(0)=Group X; X=Group*(log(Days) - 5.4); run;
The analysis of the parameter estimates is displayed in Figure 67.3. The Wald chi-square statistic for testing the null hypothesis that ![]() is 0.0158. The statistic is not statistically significant when compared to a chi-square distribution with one degree of freedom
(p = 0.8999). Thus, you can conclude that there is no evidence of an increasing or decreasing trend over time in the hazard
ratio.
is 0.0158. The statistic is not statistically significant when compared to a chi-square distribution with one degree of freedom
(p = 0.8999). Thus, you can conclude that there is no evidence of an increasing or decreasing trend over time in the hazard
ratio.
Figure 67.3: A Simple Test of Trend in the Hazard Ratio
| Analysis of Maximum Likelihood Estimates | ||||||
|---|---|---|---|---|---|---|
| Parameter | DF | Parameter Estimate |
Standard Error |
Chi-Square | Pr > ChiSq | Hazard Ratio |
| Group | 1 | -0.59976 | 0.34837 | 2.9639 | 0.0851 | 0.549 |
| X | 1 | -0.22952 | 1.82489 | 0.0158 | 0.8999 | 0.795 |