The MCMC Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin Diagnostics
Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin Diagnostics - References
Proper transformations of parameters can often improve the mixing in PROC MCMC. You already saw this in Nonlinear Poisson Regression Models, which sampled using the ![]() scale of parameters that priors that are strictly positive, such as the gamma priors. This example shows another useful transformation:
the logit transformation on parameters that take a uniform prior on [0, 1].
scale of parameters that priors that are strictly positive, such as the gamma priors. This example shows another useful transformation:
the logit transformation on parameters that take a uniform prior on [0, 1].
The data set is taken from Sharples (1990). It is used in Chaloner and Brant (1988) and Chaloner (1994) to identify outliers in the data set in a two-level hierarchical model. Congdon (2003) also uses this data set to demonstrates the same technique. This example uses the data set to illustrate how mixing can be improved using transformation and does not address the question of outlier detection as in those papers. The following statements create the data set:
data inputdata; input nobs grp y @@; ind = _n_; datalines; 1 1 24.80 2 1 26.90 3 1 26.65 4 1 30.93 5 1 33.77 6 1 63.31 1 2 23.96 2 2 28.92 3 2 28.19 4 2 26.16 5 2 21.34 6 2 29.46 1 3 18.30 2 3 23.67 3 3 14.47 4 3 24.45 5 3 24.89 6 3 28.95 1 4 51.42 2 4 27.97 3 4 24.76 4 4 26.67 5 4 17.58 6 4 24.29 1 5 34.12 2 5 46.87 3 5 58.59 4 5 38.11 5 5 47.59 6 5 44.67 ;
There are five groups (grp, ![]() ) with six observations (
) with six observations (nobs, ![]() ) in each. The two-level hierarchical model is specified as follows:
) in each. The two-level hierarchical model is specified as follows:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
with the precision parameters related to each other in the following way:
|
|
|
|
|
|
|
|
The total number of parameters in this model is eight: ![]() , and p.
, and p.
The following statements fit the model:
ods graphics on;
proc mcmc data=inputdata nmc=50000 thin=10 outpost=m1 seed=17
plot=trace;
ods select ess tracepanel;
parms p;
parms tau;
parms mu;
prior p ~ uniform(0,1);
prior tau ~ gamma(shape=0.001,iscale=0.001);
prior mu ~ normal(0,prec=0.00000001);
beginnodata;
taub = tau/p;
tauw = taub-tau;
endnodata;
random theta ~ normal(mu, prec=taub) subject=grp monitor=(theta);
model y ~ normal(theta,prec=tauw);
run;
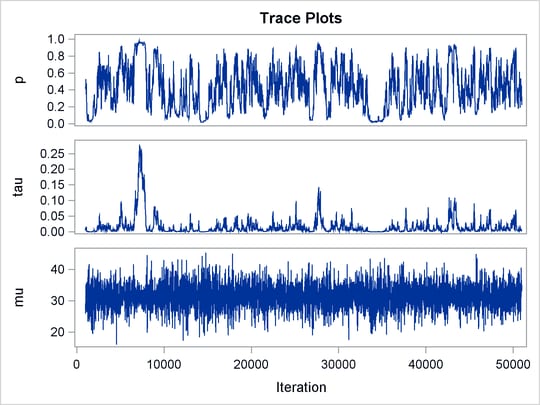
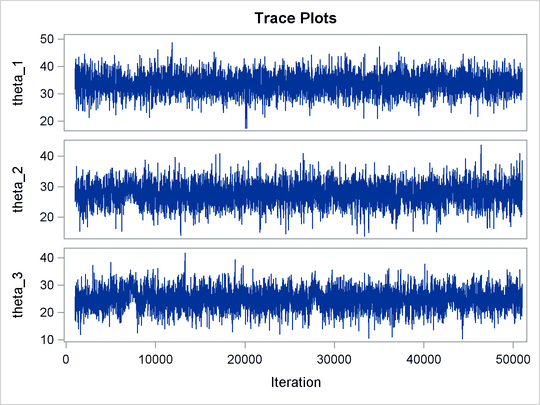
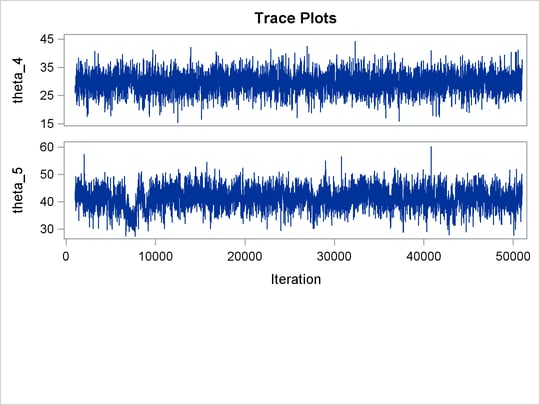
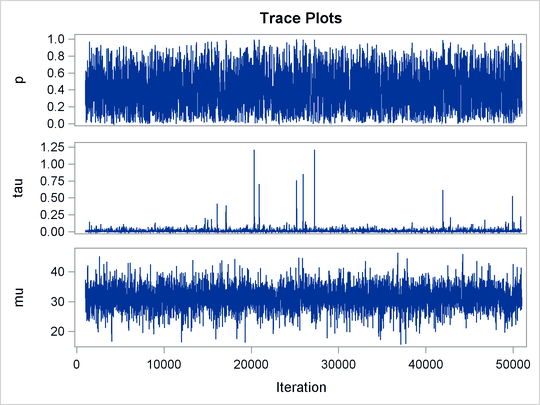
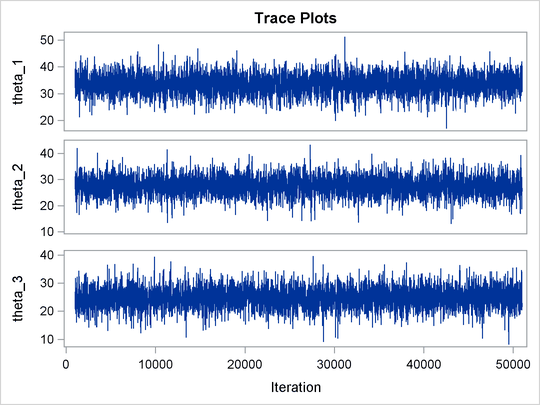
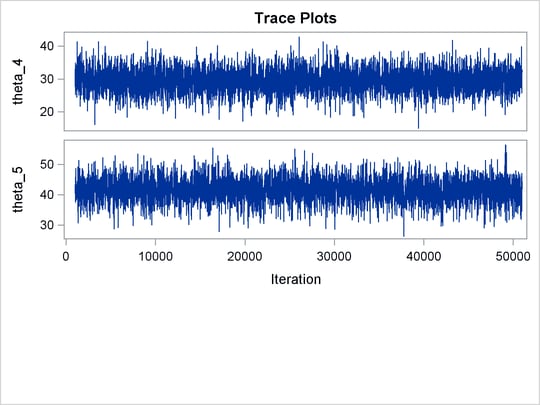
The ODS SELECT statement displays the effective sample size table and the trace plots. The ODS GRAPHICS ON statement enables
ODS Graphics. The PROC MCMC statement specifies the usual options for the procedure run and produces trace plots (PLOTS=TRACE). The three PARMS statements put three model parameters, p, tau, and mu, in three different blocks. The PRIOR statements specify the prior distributions, and the programming statements enclosed with the BEGINNODATA and ENDNODATA statements calculate the transformation to taub and tauw. The RANDOM statement specifies the random effect, its prior distribution, and the subject variable. The resulting trace plots are shown
in Output 55.20.1, and the effective sample size table is shown in Output 55.20.2.
Output 55.20.2: Bad Effective Sample Sizes
| Implement a New Sampling Algorithm |
| Effective Sample Sizes | |||
|---|---|---|---|
| Parameter | ESS | Autocorrelation Time |
Efficiency |
| p | 81.3 | 61.5342 | 0.0163 |
| tau | 61.2 | 81.7440 | 0.0122 |
| mu | 5000.0 | 1.0000 | 1.0000 |
| theta_1 | 4839.9 | 1.0331 | 0.9680 |
| theta_2 | 2739.7 | 1.8250 | 0.5479 |
| theta_3 | 1346.6 | 3.7130 | 0.2693 |
| theta_4 | 4897.5 | 1.0209 | 0.9795 |
| theta_5 | 338.1 | 14.7866 | 0.0676 |
The trace plots show that most parameters have relatively good mixing. Two exceptions appear to be p and ![]() . The trace plot of p shows a slow periodic movement. The
. The trace plot of p shows a slow periodic movement. The ![]() parameter does not have good mixing either. When the values are close to zero, the chain stays there for periods of time.
An inspection of the effective sample sizes table reveals the same conclusion: p and
parameter does not have good mixing either. When the values are close to zero, the chain stays there for periods of time.
An inspection of the effective sample sizes table reveals the same conclusion: p and ![]() have much smaller ESSs than the rest of the parameters.
have much smaller ESSs than the rest of the parameters.
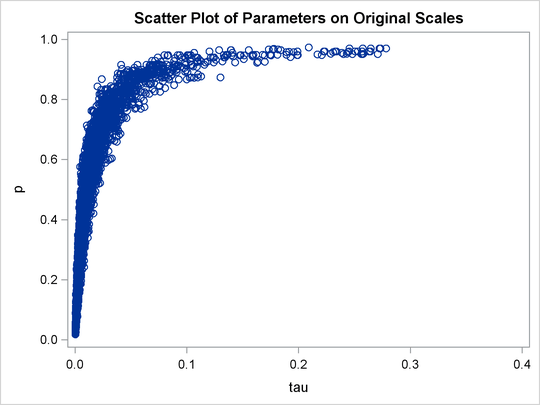
A scatter plot of the posterior samples of p and ![]() reveals why mixing is bad in these two dimensions. The following statements generate the scatter plot in Output 55.20.3:
reveals why mixing is bad in these two dimensions. The following statements generate the scatter plot in Output 55.20.3:
title 'Scatter Plot of Parameters on Original Scales'; proc sgplot data=m1; yaxis label = 'p'; xaxis label = 'tau' values=(0 to 0.4 by 0.1); scatter x = tau y = p; run;
The two parameters clearly have a nonlinear relationship. It is not surprising that the Metropolis algorithm does not work well here. The algorithm is designed for cases where the parameters are linearly related with each other.
To improve on mixing, you can sample on the log of ![]() , instead of sampling on
, instead of sampling on ![]() . The formulation is:
. The formulation is:
|
|
|
|
|
|
|
|
See the section Standard Distributions for the definitions of the gamma and egamma distributions. In addition, you can sample on the logit of p. Note that
is equivalent to
The following statements fit the same model by using transformed parameters:
proc mcmc data=inputdata nmc=50000 thin=10 outpost=m2 seed=17
monitor=(p tau mu) plot=trace;
ods select ess tracepanel;
parms ltau lgp mu ;
prior ltau ~ egamma(shape=0.001,iscale=0.001);
prior lgp ~ logistic(0,1);
prior mu ~ normal(0,prec=0.00000001);
beginnodata;
tau = exp(ltau);
p = logistic(lgp);
taub = tau/p;
tauw = taub-tau;
endnodata;
random theta ~ normal(mu, prec=taub) subject=grp monitor=(theta);
model y ~ normal(theta,prec=tauw);
run;
The variable lgp is the logit transformation of p, and ltau is the log transformation of ![]() . The prior for
. The prior for ltau is egamma, and the prior for lgp is logistic. The TAU and P assignment statements transform the parameters back to their original scales. The rest of the programs remain
unchanged. Trace plots (Output 55.20.4) and effective sample size (Output 55.20.5) both show significant improvements in the mixing for both p and ![]() .
.
Output 55.20.5: Effective Sample Sizes after Transformation
| Effective Sample Sizes | |||
|---|---|---|---|
| Parameter | ESS | Autocorrelation Time |
Efficiency |
| p | 3119.4 | 1.6029 | 0.6239 |
| tau | 2588.0 | 1.9320 | 0.5176 |
| mu | 5000.0 | 1.0000 | 1.0000 |
| theta_1 | 4866.0 | 1.0275 | 0.9732 |
| theta_2 | 5244.5 | 0.9534 | 1.0489 |
| theta_3 | 5000.0 | 1.0000 | 1.0000 |
| theta_4 | 5000.0 | 1.0000 | 1.0000 |
| theta_5 | 4054.8 | 1.2331 | 0.8110 |
The following statements generate Output 55.20.6 and Output 55.20.7:
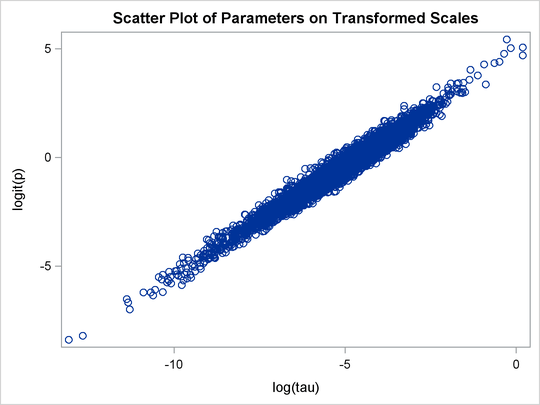
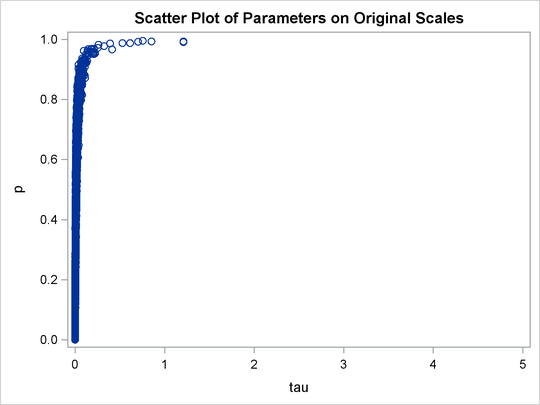
title 'Scatter Plot of Parameters on Transformed Scales'; proc sgplot data=m2; yaxis label = 'logit(p)'; xaxis label = 'log(tau)'; scatter x = ltau y = lgp; run; title 'Scatter Plot of Parameters on Original Scales'; proc sgplot data=m2; yaxis label = 'p'; xaxis label = 'tau' values=(0 to 5.0 by 1); scatter x = tau y = p; run; ods graphics off;
The scatter plot of ![]() versus
versus ![]() shows a linear relationship between the two transformed parameters, and this explains the improvement in mixing. In addition,
the transformations also help the Markov chain better explore in the original parameter space. Output 55.20.7 shows a scatter plot of
shows a linear relationship between the two transformed parameters, and this explains the improvement in mixing. In addition,
the transformations also help the Markov chain better explore in the original parameter space. Output 55.20.7 shows a scatter plot of ![]() versus p. The plot is similar to Output 55.20.3. However, note that
versus p. The plot is similar to Output 55.20.3. However, note that tau has a far longer tail in Output 55.20.7, extending all the way to 5 as opposed to 0.15 in Output 55.20.3. This means that the second Markov chain can explore this dimension of the parameter more efficiently, and as a result, you
are able to draw more precise inference with an equal number of simulations.