Linear Regression: The REG Procedure
The REG procedure is a general-purpose procedure for linear regression that does the following:
-
handles multiple regression models
-
provides nine model-selection methods
-
allows interactive changes both in the model and in the data used to fit the model
-
allows linear equality restrictions on parameters
-
tests linear hypotheses and multivariate hypotheses
-
produces collinearity diagnostics, influence diagnostics, and partial regression leverage plots
-
saves estimates, predicted values, residuals, confidence limits, and other diagnostic statistics in output SAS data sets
-
generates plots of data and of various statistics
-
“paints” or highlights scatter plots to identify particular observations or groups of observations
-
uses, optionally, correlations or crossproducts for input
Model-Selection Methods in Linear Regression Models
An important step in building statistical models is to determine which effects and variables affect the response variable and to form a model that fits the data well without incurring the negative effects of overfitting the model. Models that are overfit—that is, contain too many regressor variables and unimportant regressor variables—have a tendency to be too closely molded to a a particular set of data, have unstable regression coefficients, and possibly have poor predictive precision. In situations where many potential regressor variables are available for inclusion in a regression model, guided, numerical variable-selection methods offer one approach to model building.
The model-selection techniques for linear regression models implemented in the REG procedure are as follows:
- NONE
-
specifies that no selection be made. This method is the default and uses the full model given in the MODEL statement to fit the linear regression.
- FORWARD
-
specifies that variables be selected based on a forward-selection algorithm. This method starts with no variables in the model and adds variables one by one to the model. At each step, the variable added is the one that most improves the fit of the model. You can also specify groups of variables to treat as a unit during the selection process. An option enables you to specify the criterion for inclusion.
- BACKWARD
-
specifies that variables be selected based on a backward-elimination algorithm. This method starts with a full model and eliminates variables one by one from the model. At each step, the variable with the smallest contribution to the model is deleted. You can also specify groups of variables to treat as a unit during the selection process. An option enables you to specify the criterion for exclusion.
- STEPWISE
-
specifies that variables be selected for the model based on a stepwise-regression algorithm, which combines forward-selection and backward-elimination steps. This method is a modification of the forward-selection method in that variables already in the model do not necessarily stay there. You can also specify groups of variables to treat as a unit during the selection process. Again, options enable you to specify criteria for entry into the model and for remaining in the model.
- MAXR
-
specifies that model formation be based on the maximum R square improvement. This method tries to find the best one-variable model, the best two-variable model, and so on. The MAXR method differs from the STEPWISE method in that many more models are evaluated. The MAXR method considers all possible variable exchanges before making any exchange. The STEPWISE method might remove the “worst” variable without considering what the “best” remaining variable might accomplish, whereas MAXR would consider what the “best” remaining variable might accomplish. Consequently, model building based on the maximum R square improvement typically takes much longer to run than stepwise model building.
- MINR
-
specifies that model formation be based on the minimum R square improvement. This method closely resembles MAXR, but the switch chosen is the one that produces the smallest increase in R square.
- RSQUARE
-
finds a specified number of models having the highest R square in each of a range of model sizes.
- CP
-
finds a specified number of models with the lowest
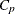 within a range of model sizes.
within a range of model sizes.
- ADJRSQ
-
finds a specified number of models having the highest adjusted R square within a range of model sizes.
The GLMSELECT procedure has been specifically designed for the purpose of model building in linear models. In addition to having a wider array of selection methods and criteria compared to the REG procedure, the GLMSELECT procedure also supports classification variables. See Chapter 45: The GLMSELECT Procedure, for more information.
Regression with the REG and GLM Procedures
In terms of the assumptions about the basic model and the estimation principles, the REG and GLM procedures are very closely related. Both procedures estimate parameters by ordinary or weighted least squares and assume homoscedastic, uncorrelated model errors with zero mean. An assumption of normality of the model errors is not necessary for parameter estimation, but it is implied in confirmatory inference based on the parameter estimates—that is, the computation of tests, p-values, and confidence and prediction intervals.
The GLM procedure supports a CLASS statement for the levelization of classification variables; see the section Parameterization of Model Effects in Chapter 19: Shared Concepts and Topics, on the parameterization of classification variables in statistical models. Classification variables are accommodated in the REG procedure by the inclusion of the necessary dummy regressor variables.
Most of the statistics based on predicted and residual values that are available in PROC REG are also available in PROC GLM. However, PROC GLM does not produce collinearity diagnostics, influence diagnostics, or scatter plots. In addition, PROC GLM allows only one model and fits the full model.
Both procedures are interactive, in that they do not stop after processing a RUN statement. The procedures accept statements until a QUIT statement is submitted.