The GENMOD Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement
PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement -
Details
 Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics
Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics -
Examples
 Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson Regression
Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson Regression - References
Bayesian Analysis of a Linear Regression Model
Neter et al. (1996) describe a study of 54 patients undergoing a certain kind of liver operation in a surgical unit. The data set Surg contains survival time and certain covariates for each patient. Observations for the first 20 patients in the data set Surg are shown in Figure 40.7.
Figure 40.7: Surgical Unit Data
| Obs | x1 | x2 | x3 | x4 | y | logy | Logx1 |
|---|---|---|---|---|---|---|---|
| 1 | 6.7 | 62 | 81 | 2.59 | 200 | 2.3010 | 1.90211 |
| 2 | 5.1 | 59 | 66 | 1.70 | 101 | 2.0043 | 1.62924 |
| 3 | 7.4 | 57 | 83 | 2.16 | 204 | 2.3096 | 2.00148 |
| 4 | 6.5 | 73 | 41 | 2.01 | 101 | 2.0043 | 1.87180 |
| 5 | 7.8 | 65 | 115 | 4.30 | 509 | 2.7067 | 2.05412 |
| 6 | 5.8 | 38 | 72 | 1.42 | 80 | 1.9031 | 1.75786 |
| 7 | 5.7 | 46 | 63 | 1.91 | 80 | 1.9031 | 1.74047 |
| 8 | 3.7 | 68 | 81 | 2.57 | 127 | 2.1038 | 1.30833 |
| 9 | 6.0 | 67 | 93 | 2.50 | 202 | 2.3054 | 1.79176 |
| 10 | 3.7 | 76 | 94 | 2.40 | 203 | 2.3075 | 1.30833 |
| 11 | 6.3 | 84 | 83 | 4.13 | 329 | 2.5172 | 1.84055 |
| 12 | 6.7 | 51 | 43 | 1.86 | 65 | 1.8129 | 1.90211 |
| 13 | 5.8 | 96 | 114 | 3.95 | 830 | 2.9191 | 1.75786 |
| 14 | 5.8 | 83 | 88 | 3.95 | 330 | 2.5185 | 1.75786 |
| 15 | 7.7 | 62 | 67 | 3.40 | 168 | 2.2253 | 2.04122 |
| 16 | 7.4 | 74 | 68 | 2.40 | 217 | 2.3365 | 2.00148 |
| 17 | 6.0 | 85 | 28 | 2.98 | 87 | 1.9395 | 1.79176 |
| 18 | 3.7 | 51 | 41 | 1.55 | 34 | 1.5315 | 1.30833 |
| 19 | 7.3 | 68 | 74 | 3.56 | 215 | 2.3324 | 1.98787 |
| 20 | 5.6 | 57 | 87 | 3.02 | 172 | 2.2355 | 1.72277 |
Consider the model
|
|
where Y is the survival time, LogX1 is log(blood-clotting score), X2 is a prognostic index, X3 is an enzyme function test score, X4 is a liver function test score, and ![]() is an
is an ![]() error term.
error term.
A question of scientific interest is whether blood clotting score has a positive effect on survival time. Using PROC GENMOD,
you can obtain a maximum likelihood estimate of the coefficient and construct a null point hypothesis to test whether ![]() is equal to 0. However, if you are interested in finding the probability that the coefficient is positive, Bayesian analysis
offers a convenient alternative. You can use Bayesian analysis to directly estimate the conditional probability,
is equal to 0. However, if you are interested in finding the probability that the coefficient is positive, Bayesian analysis
offers a convenient alternative. You can use Bayesian analysis to directly estimate the conditional probability, ![]() , using the posterior distribution samples, which are produced as part of the output by PROC GENMOD.
, using the posterior distribution samples, which are produced as part of the output by PROC GENMOD.
The example that follows shows how to use PROC GENMOD to carry out a Bayesian analysis of the linear model with a normal error
term. The SEED= option is specified to maintain reproducibility; no other options are specified in the BAYES statement. By
default, a uniform prior distribution is assumed on the regression coefficients. The uniform prior is a flat prior on the
real line with a distribution that reflects ignorance of the location of the parameter, placing equal likelihood on all possible
values the regression coefficient can take. Using the uniform prior in the following example, you would expect the Bayesian
estimates to resemble the classical results of maximizing the likelihood. If you can elicit an informative prior distribution
for the regression coefficients, you should use the COEFFPRIOR= option to specify it. A default noninformative gamma prior
is used for the scale parameter ![]() .
.
You should make sure that the posterior distribution samples have achieved convergence before using them for Bayesian inference. PROC GENMOD produces three convergence diagnostics by default. If ODS Graphics is enabled as specified in the following SAS statements, diagnostic plots are also displayed. See the section Assessing Markov Chain Convergence for more information about convergence diagnostics and their interpretation.
Summary statistics of the posterior distribution samples are produced by default. However, these statistics might not be sufficient
for carrying out your Bayesian inference, and further processing of the posterior samples might be necessary. The following
SAS statements request the Bayesian analysis, and the OUTPOST= option saves the samples in the SAS data set PostSurg for further processing:
proc genmod data=Surg; model y = Logx1 X2 X3 X4 / dist=normal; bayes seed=1 OutPost=PostSurg; run;
The results of this analysis are shown in the following figures.
The “Model Information” table in Figure 40.8 summarizes information about the model you fit and the size of the simulation.
Figure 40.8: Model Information
| Model Information | ||
|---|---|---|
| Data Set | WORK.SURG | |
| Burn-In Size | 2000 | |
| MC Sample Size | 10000 | |
| Thinning | 1 | |
| Sampling Algorithm | Conjugate | |
| Distribution | Normal | |
| Link Function | Identity | |
| Dependent Variable | y | Survival Time |
The “Analysis of Maximum Likelihood Parameter Estimates” table in Figure 40.9 summarizes maximum likelihood estimates of the model parameters.
Figure 40.9: Maximum Likelihood Parameter Estimates
| Analysis Of Maximum Likelihood Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | Wald 95% Confidence Limits | |
| Intercept | 1 | -730.559 | 85.4333 | -898.005 | -563.112 |
| Logx1 | 1 | 171.8758 | 38.2250 | 96.9561 | 246.7954 |
| x2 | 1 | 4.3019 | 0.5566 | 3.2109 | 5.3929 |
| x3 | 1 | 4.0309 | 0.4996 | 3.0517 | 5.0100 |
| x4 | 1 | 18.1377 | 12.0721 | -5.5232 | 41.7986 |
| Scale | 1 | 59.8591 | 5.7599 | 49.5705 | 72.2832 |
| Note: | The scale parameter was estimated by maximum likelihood. |
Since no prior distributions for the regression coefficients were specified, the default noninformative uniform distributions shown in the “Uniform Prior for Regression Coefficients” table in Figure 40.10 are used. Noninformative priors are appropriate if you have no prior knowledge of the likely range of values of the parameters, and if you want to make probability statements about the parameters or functions of the parameters. See, for example, Ibrahim, Chen, and Sinha (2001) for more information about choosing prior distributions.
Figure 40.10: Regression Coefficient Priors
| Uniform Prior for Regression Coefficients |
|
|---|---|
| Parameter | Prior |
| Intercept | Constant |
| Logx1 | Constant |
| x2 | Constant |
| x3 | Constant |
| x4 | Constant |
The default noninformative improper prior distribution for the normal dispersion parameter is shown in the “Independent Prior Distributions for Model Parameters” table in Figure 40.11.
Figure 40.11: Scale Parameter Prior
| Independent Prior Distributions for Model Parameters |
|
|---|---|
| Parameter | Prior Distribution |
| Dispersion | Improper |
By default, the maximum likelihood estimates of the regression parameters are used as the starting values for the simulation when noninformative prior distributions are used. These are listed in the “Initial Values and Seeds” table in Figure 40.12.
Figure 40.12: MCMC Initial Values and Seeds
| Initial Values of the Chain | |||||||
|---|---|---|---|---|---|---|---|
| Chain | Seed | Intercept | Logx1 | x2 | x3 | x4 | Dispersion |
| 1 | 1 | -730.559 | 171.8758 | 4.301896 | 4.030878 | 18.1377 | 3449.176 |
Summary statistics for the posterior sample are displayed in the “Fit Statistics,” “Descriptive Statistics for the Posterior Sample,” “Interval Statistics for the Posterior Sample,” and “Posterior Correlation Matrix” tables in Figure 40.13, Figure 40.14, Figure 40.15, and Figure 40.16, respectively.
Figure 40.13: Fit Statistics
| Fit Statistics | |
|---|---|
| DIC (smaller is better) | 607.796 |
| pD (effective number of parameters) | 6.062 |
Figure 40.14: Descriptive Statistics
| Posterior Summaries | ||||||
|---|---|---|---|---|---|---|
| Parameter | N | Mean | Standard Deviation |
Percentiles | ||
| 25% | 50% | 75% | ||||
| Intercept | 10000 | -730.0 | 91.2102 | -789.6 | -729.6 | -670.5 |
| Logx1 | 10000 | 171.7 | 40.6455 | 144.2 | 171.6 | 198.6 |
| x2 | 10000 | 4.2988 | 0.5952 | 3.9029 | 4.2919 | 4.6903 |
| x3 | 10000 | 4.0308 | 0.5359 | 3.6641 | 4.0267 | 4.3921 |
| x4 | 10000 | 18.0858 | 12.9123 | 9.4471 | 18.1230 | 26.8141 |
| Dispersion | 10000 | 4113.1 | 867.7 | 3497.2 | 3995.9 | 4606.4 |
Figure 40.15: Interval Statistics
| Posterior Intervals | |||||
|---|---|---|---|---|---|
| Parameter | Alpha | Equal-Tail Interval | HPD Interval | ||
| Intercept | 0.050 | -908.6 | -549.8 | -906.9 | -549.1 |
| Logx1 | 0.050 | 91.9723 | 252.5 | 94.1279 | 254.0 |
| x2 | 0.050 | 3.1091 | 5.4778 | 3.1705 | 5.5167 |
| x3 | 0.050 | 2.9803 | 5.1031 | 2.9227 | 5.0343 |
| x4 | 0.050 | -7.3043 | 43.6387 | -8.8440 | 41.8229 |
| Dispersion | 0.050 | 2741.5 | 6096.6 | 2540.1 | 5810.0 |
Figure 40.16: Posterior Sample Correlation Matrix
| Posterior Correlation Matrix | ||||||
|---|---|---|---|---|---|---|
| Parameter | Intercept | Logx1 | x2 | x3 | x4 | Dispersion |
| Intercept | 1.000 | -0.857 | -0.579 | -0.712 | 0.582 | 0.000 |
| Logx1 | -0.857 | 1.000 | 0.286 | 0.491 | -0.640 | 0.007 |
| x2 | -0.579 | 0.286 | 1.000 | 0.302 | -0.489 | -0.009 |
| x3 | -0.712 | 0.491 | 0.302 | 1.000 | -0.618 | -0.006 |
| x4 | 0.582 | -0.640 | -0.489 | -0.618 | 1.000 | 0.003 |
| Dispersion | 0.000 | 0.007 | -0.009 | -0.006 | 0.003 | 1.000 |
Since noninformative prior distributions were used, the posterior sample means, standard deviations, and interval statistics shown in Figure 40.13 and Figure 40.14 are consistent with the maximum likelihood estimates shown in Figure 40.9.
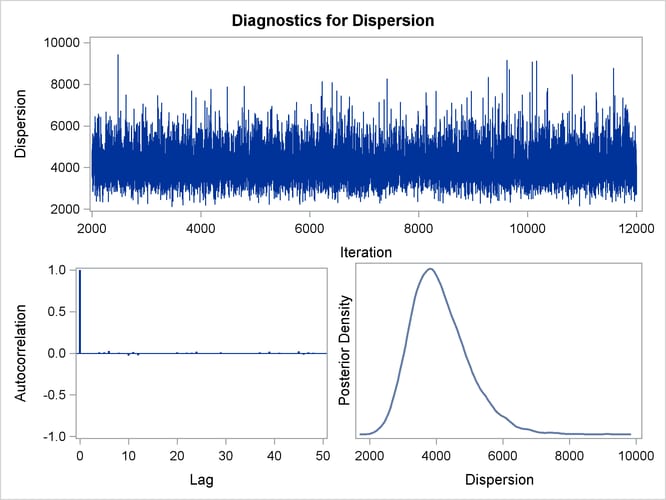
By default, PROC GENMOD computes three convergence diagnostics: the lag1, lag5, lag10, and lag50 autocorrelations (Figure 40.17); Geweke diagnostic statistics (Figure 40.18); and effective sample sizes (Figure 40.19). There is no indication that the Markov chain has not converged. See the section Assessing Markov Chain Convergence for more information about convergence diagnostics and their interpretation.
Figure 40.17: Posterior Sample Autocorrelations
| Posterior Autocorrelations | ||||
|---|---|---|---|---|
| Parameter | Lag 1 | Lag 5 | Lag 10 | Lag 50 |
| Intercept | -0.0059 | -0.0037 | -0.0152 | 0.0010 |
| Logx1 | -0.0002 | -0.0064 | -0.0066 | -0.0054 |
| x2 | -0.0120 | -0.0026 | -0.0267 | -0.0168 |
| x3 | 0.0036 | 0.0033 | -0.0035 | 0.0004 |
| x4 | 0.0034 | -0.0064 | 0.0083 | -0.0124 |
| Dispersion | -0.0011 | 0.0091 | -0.0279 | 0.0037 |
Figure 40.18: Geweke Diagnostic Statistics
| Geweke Diagnostics | ||
|---|---|---|
| Parameter | z | Pr > |z| |
| Intercept | -1.0815 | 0.2795 |
| Logx1 | 1.6667 | 0.0956 |
| x2 | 0.0977 | 0.9222 |
| x3 | 0.2506 | 0.8021 |
| x4 | -1.1082 | 0.2678 |
| Dispersion | 0.2451 | 0.8064 |
Figure 40.19: Effective Sample Sizes
| Effective Sample Sizes | |||
|---|---|---|---|
| Parameter | ESS | Autocorrelation Time |
Efficiency |
| Intercept | 10000.0 | 1.0000 | 1.0000 |
| Logx1 | 10000.0 | 1.0000 | 1.0000 |
| x2 | 10245.2 | 0.9761 | 1.0245 |
| x3 | 10000.0 | 1.0000 | 1.0000 |
| x4 | 10000.0 | 1.0000 | 1.0000 |
| Dispersion | 10000.0 | 1.0000 | 1.0000 |
Trace, autocorrelation, and density plots for the seven model parameters, shown in Figure 40.20 through Figure 40.25, are useful in diagnosing whether the Markov chain of posterior samples has converged. These plots show no evidence that the chain has not converged. See the section Visual Analysis via Trace Plots for help with interpreting these diagnostic plots.
Figure 40.20: Diagnostic Plots for Intercept
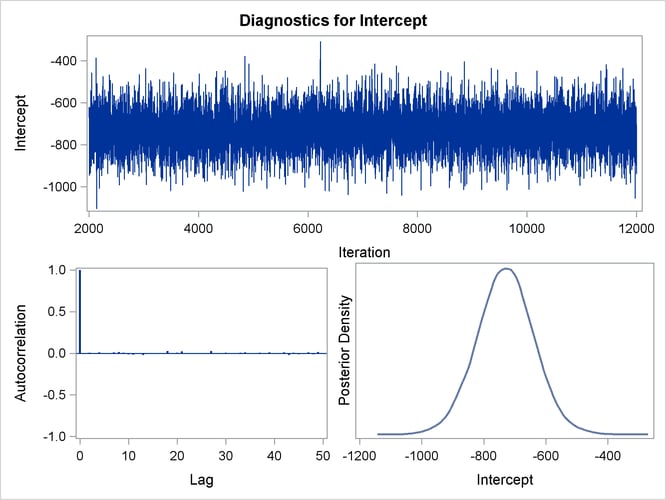
Figure 40.21: Diagnostic Plots for logX1
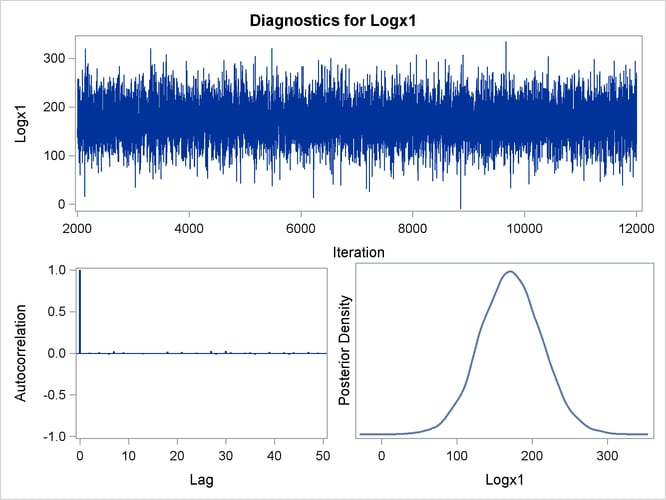
Figure 40.22: Diagnostic Plots for X2
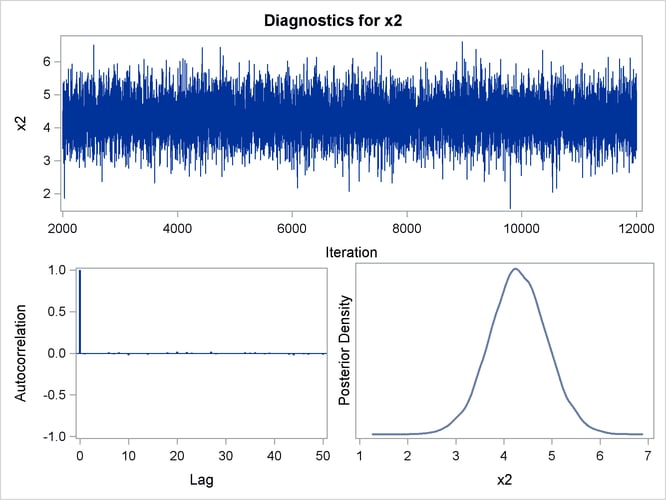
Figure 40.23: Diagnostic Plots for X3
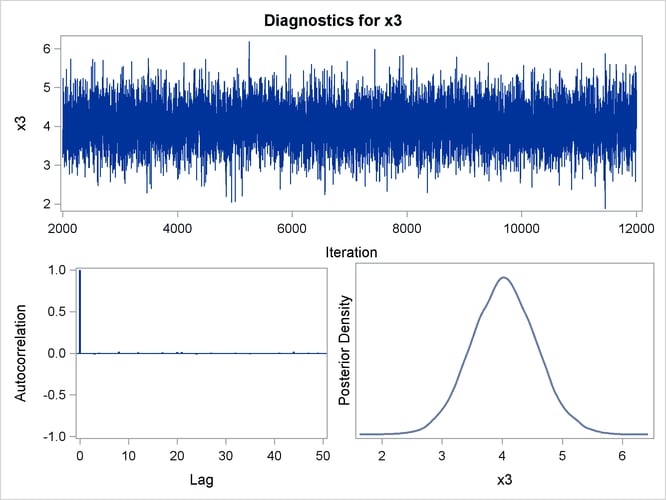
Figure 40.24: Diagnostic Plots for X4
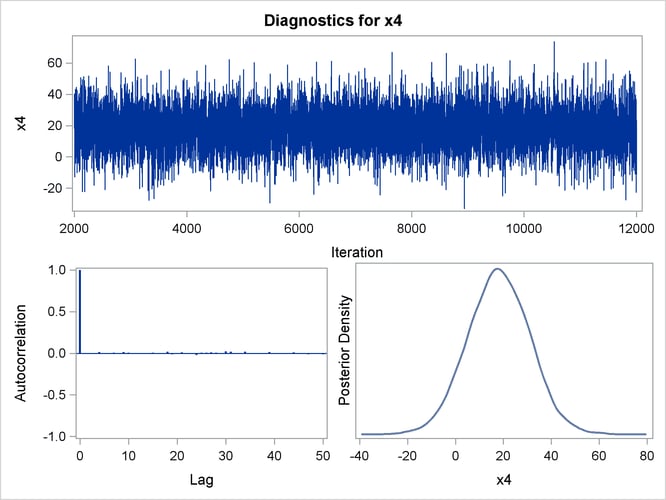
Figure 40.25: Diagnostic Plots for X5
Suppose, for illustration, a question of scientific interest is whether blood clotting score has a positive effect on survival
time. Since the model parameters are regarded as random quantities in a Bayesian analysis, you can answer this question by
estimating the conditional probability of ![]() being positive, given the data,
being positive, given the data, ![]() , from the posterior distribution samples. The following SAS statements compute the estimate of the probability of
, from the posterior distribution samples. The following SAS statements compute the estimate of the probability of ![]() being positive:
being positive:
data Prob; set PostSurg; Indicator = (logX1 > 0); label Indicator= 'log(Blood Clotting Score) > 0'; run; proc Means data = Prob(keep=Indicator) n mean; run;
As shown in Figure 40.26, there is a 1.00 probability of a positive relationship between the logarithm of a blood clotting score and survival time, adjusted for the other covariates.
Figure 40.26: Probability That ![]()
| Analysis Variable : Indicator log(Blood Clotting Score) > 0 |
|
|---|---|
| N | Mean |
| 10000 | 0.9999000 |