The TRANSREG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Model Statement Usage Box-Cox Transformations Using Splines and Knots Scoring Spline Variables Linear and Nonlinear Regression Functions Simultaneously Fitting Two Regression Functions Penalized B-Splines Smoothing Splines Smoothing Splines Changes and Enhancements Iteration History Changes and Enhancements ANOVA Codings Missing Values Missing Values, UNTIE, and Hypothesis Tests Controlling the Number of Iterations Using the REITERATE Algorithm Option Avoiding Constant Transformations Constant Variables Character OPSCORE Variables Convergence and Degeneracies Implicit and Explicit Intercepts Passive Observations Point Models Redundancy Analysis Optimal Scaling OPSCORE, MONOTONE, UNTIE, and LINEAR Transformations SPLINE and MSPLINE Transformations Specifying the Number of Knots SPLINE, BSPLINE, and PSPLINE Comparisons Hypothesis Tests Output Data Set OUTTEST= Output Data Set Computational Resources Unbalanced ANOVA without CLASS Variables Hypothesis Tests for Simple Univariate Models Hypothesis Tests with Monotonicity Constraints Hypothesis Tests with Dependent Variable Transformations Hypothesis Tests with One-Way ANOVA Using the DESIGN Output Option Discrete Choice Experiments: DESIGN, NORESTORE, NOZERO Centering Displayed Output ODS Table Names ODS Graphics
Model Statement Usage Box-Cox Transformations Using Splines and Knots Scoring Spline Variables Linear and Nonlinear Regression Functions Simultaneously Fitting Two Regression Functions Penalized B-Splines Smoothing Splines Smoothing Splines Changes and Enhancements Iteration History Changes and Enhancements ANOVA Codings Missing Values Missing Values, UNTIE, and Hypothesis Tests Controlling the Number of Iterations Using the REITERATE Algorithm Option Avoiding Constant Transformations Constant Variables Character OPSCORE Variables Convergence and Degeneracies Implicit and Explicit Intercepts Passive Observations Point Models Redundancy Analysis Optimal Scaling OPSCORE, MONOTONE, UNTIE, and LINEAR Transformations SPLINE and MSPLINE Transformations Specifying the Number of Knots SPLINE, BSPLINE, and PSPLINE Comparisons Hypothesis Tests Output Data Set OUTTEST= Output Data Set Computational Resources Unbalanced ANOVA without CLASS Variables Hypothesis Tests for Simple Univariate Models Hypothesis Tests with Monotonicity Constraints Hypothesis Tests with Dependent Variable Transformations Hypothesis Tests with One-Way ANOVA Using the DESIGN Output Option Discrete Choice Experiments: DESIGN, NORESTORE, NOZERO Centering Displayed Output ODS Table Names ODS Graphics -
Examples

- References
Example 93.4 Nonmetric Conjoint Analysis of Tire Data
This example uses PROC TRANSREG to perform a nonmetric conjoint analysis of tire preference data. Conjoint analysis decomposes rank-ordered evaluation judgments of products or services into components based on qualitative product attributes. For each level of each attribute of interest, a numerical "part-worth utility" value is computed. The sum of the part-worth utilities for each product is an estimate of the utility for that product. The goal is to compute part-worth utilities such that the product utilities are as similar as possible to the original rank ordering. (This example is a greatly simplified introductory example.)
The stimuli for the experiment are 18 hypothetical tires. The stimuli represent different brands (Goodstone, Pirogi, Machismo),1 prices ($69.99, $74.99, $79.99), expected tread life (50,000, 60,000, 70,000 miles), and road hazard insurance plans (Yes, No). There are  possible combinations. From these, 18 combinations are selected that form an efficient experimental design for a main-effects model. The combinations are then ranked from 1 (most preferred) to 18 (least preferred). In this simple example, there is one set of rankings. A real conjoint study would have many more.
possible combinations. From these, 18 combinations are selected that form an efficient experimental design for a main-effects model. The combinations are then ranked from 1 (most preferred) to 18 (least preferred). In this simple example, there is one set of rankings. A real conjoint study would have many more.
First, the FORMAT procedure is used to specify the meanings of the factor levels, which are entered as numbers in the DATA step along with the ranks. PROC TRANSREG is used to perform the conjoint analysis. A maximum of 50 iterations is requested. The specification monotone(Rank / reflect) in the MODEL statement requests that the dependent variable Rank should be monotonically transformed and reflected so that positive utilities mean high preference. The variables Brand, Price, Life, and Hazard are designated as CLASS variables, and the part-worth utilities are constrained by ZERO=SUM to sum to zero within each factor. The UTILITIES a-option displays the conjoint analysis results.
The importance column of the utilities table shows that price is the most important attribute in determining preference (57%), followed by expected tread life (18%), brand (15%), and road hazard insurance (10%). Looking at the utilities table for the maximum part-worth utility within each attribute, you see from the results that the most preferred combination is Pirogi brand tires, at $69.99, with a 70,000-mile expected tread life and road hazard insurance. This product is not actually in the data set. The sum of the part-worth utilities for this combination is as follows:
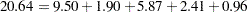 |
The following statements produce Output 93.4.1.
title 'Nonmetric Conjoint Analysis of Ranks';
proc format;
value BrandF
1 = 'Goodstone'
2 = 'Pirogi '
3 = 'Machismo ';
value PriceF
1 = '$69.99'
2 = '$74.99'
3 = '$79.99';
value LifeF
1 = '50,000'
2 = '60,000'
3 = '70,000';
value HazardF
1 = 'Yes'
2 = 'No ';
run;
data Tires; input Brand Price Life Hazard Rank; format Brand BrandF9. Price PriceF9. Life LifeF6. Hazard HazardF3.; datalines; 1 1 2 1 3 1 1 3 2 2 1 2 1 2 14 1 2 2 2 10 1 3 1 1 17 1 3 3 1 12 2 1 1 2 7 2 1 3 2 1 2 2 1 1 8 2 2 3 1 5 2 3 2 1 13 2 3 2 2 16 3 1 1 1 6 3 1 2 1 4 3 2 2 2 15 3 2 3 1 9 3 3 1 2 18 3 3 3 2 11 ;
proc transreg maxiter=50 utilities short;
ods select TestsNote ConvergenceStatus FitStatistics Utilities;
model monotone(Rank / reflect) =
class(Brand Price Life Hazard / zero=sum);
output ireplace predicted;
run;
proc print label;
var Rank TRank PRank Brand Price Life Hazard;
label PRank = 'Predicted Ranks';
run;
| Nonmetric Conjoint Analysis of Ranks |
| Monotone(Rank) |
|---|
| Algorithm converged. |
| Root MSE | 0.49759 | R-Square | 0.9949 |
|---|---|---|---|
| Dependent Mean | 9.50000 | Adj R-Sq | 0.9913 |
| Coeff Var | 5.23783 |
| Utilities Table Based on the Usual Degrees of Freedom | ||||
|---|---|---|---|---|
| Label | Utility | Standard Error | Importance (% Utility Range) |
Variable |
| Intercept | 9.5000 | 0.11728 | Intercept | |
| Brand Goodstone | -1.1718 | 0.16586 | 15.463 | Class.BrandGoodstone |
| Brand Pirogi | 1.8980 | 0.16586 | Class.BrandPirogi | |
| Brand Machismo | -0.7262 | 0.16586 | Class.BrandMachismo | |
| Price $69.99 | 5.8732 | 0.16586 | 56.517 | Class.Price_69_99 |
| Price $74.99 | -0.5261 | 0.16586 | Class.Price_74_99 | |
| Price $79.99 | -5.3471 | 0.16586 | Class.Price_79_99 | |
| Life 50,000 | -1.2350 | 0.16586 | 18.361 | Class.Life50_000 |
| Life 60,000 | -1.1751 | 0.16586 | Class.Life60_000 | |
| Life 70,000 | 2.4101 | 0.16586 | Class.Life70_000 | |
| Hazard Yes | 0.9588 | 0.11728 | 9.659 | Class.HazardYes |
| Hazard No | -0.9588 | 0.11728 | Class.HazardNo | |
| The standard errors are not adjusted for the fact that the dependent variable was transformed and so are generally liberal (too small). | ||||
| Nonmetric Conjoint Analysis of Ranks |
| Obs | Rank | Rank Transformation | Predicted Ranks | Brand | Price | Life | Hazard |
|---|---|---|---|---|---|---|---|
| 1 | 3 | 14.4462 | 13.9851 | Goodstone | $69.99 | 60,000 | Yes |
| 2 | 2 | 15.6844 | 15.6527 | Goodstone | $69.99 | 70,000 | No |
| 3 | 14 | 5.7229 | 5.6083 | Goodstone | $74.99 | 50,000 | No |
| 4 | 10 | 5.7229 | 5.6682 | Goodstone | $74.99 | 60,000 | No |
| 5 | 17 | 2.6699 | 2.7049 | Goodstone | $79.99 | 50,000 | Yes |
| 6 | 12 | 5.7229 | 6.3500 | Goodstone | $79.99 | 70,000 | Yes |
| 7 | 7 | 14.4462 | 15.0774 | Pirogi | $69.99 | 50,000 | No |
| 8 | 1 | 18.7699 | 18.7225 | Pirogi | $69.99 | 70,000 | No |
| 9 | 8 | 11.1143 | 10.5957 | Pirogi | $74.99 | 50,000 | Yes |
| 10 | 5 | 14.4462 | 14.2408 | Pirogi | $74.99 | 70,000 | Yes |
| 11 | 13 | 5.7229 | 5.8346 | Pirogi | $79.99 | 60,000 | Yes |
| 12 | 16 | 3.8884 | 3.9170 | Pirogi | $79.99 | 60,000 | No |
| 13 | 6 | 14.4462 | 14.3708 | Machismo | $69.99 | 50,000 | Yes |
| 14 | 4 | 14.4462 | 14.4307 | Machismo | $69.99 | 60,000 | Yes |
| 15 | 15 | 5.7229 | 6.1139 | Machismo | $74.99 | 60,000 | No |
| 16 | 9 | 11.1143 | 11.6166 | Machismo | $74.99 | 70,000 | Yes |
| 17 | 18 | 1.1905 | 1.2330 | Machismo | $79.99 | 50,000 | No |
| 18 | 11 | 5.7229 | 4.8780 | Machismo | $79.99 | 70,000 | No |