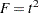The TRANSREG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Model Statement Usage Box-Cox Transformations Using Splines and Knots Scoring Spline Variables Linear and Nonlinear Regression Functions Simultaneously Fitting Two Regression Functions Penalized B-Splines Smoothing Splines Smoothing Splines Changes and Enhancements Iteration History Changes and Enhancements ANOVA Codings Missing Values Missing Values, UNTIE, and Hypothesis Tests Controlling the Number of Iterations Using the REITERATE Algorithm Option Avoiding Constant Transformations Constant Variables Character OPSCORE Variables Convergence and Degeneracies Implicit and Explicit Intercepts Passive Observations Point Models Redundancy Analysis Optimal Scaling OPSCORE, MONOTONE, UNTIE, and LINEAR Transformations SPLINE and MSPLINE Transformations Specifying the Number of Knots SPLINE, BSPLINE, and PSPLINE Comparisons Hypothesis Tests Output Data Set OUTTEST= Output Data Set Computational Resources Unbalanced ANOVA without CLASS Variables Hypothesis Tests for Simple Univariate Models Hypothesis Tests with Monotonicity Constraints Hypothesis Tests with Dependent Variable Transformations Hypothesis Tests with One-Way ANOVA Using the DESIGN Output Option Discrete Choice Experiments: DESIGN, NORESTORE, NOZERO Centering Displayed Output ODS Table Names ODS Graphics
Model Statement Usage Box-Cox Transformations Using Splines and Knots Scoring Spline Variables Linear and Nonlinear Regression Functions Simultaneously Fitting Two Regression Functions Penalized B-Splines Smoothing Splines Smoothing Splines Changes and Enhancements Iteration History Changes and Enhancements ANOVA Codings Missing Values Missing Values, UNTIE, and Hypothesis Tests Controlling the Number of Iterations Using the REITERATE Algorithm Option Avoiding Constant Transformations Constant Variables Character OPSCORE Variables Convergence and Degeneracies Implicit and Explicit Intercepts Passive Observations Point Models Redundancy Analysis Optimal Scaling OPSCORE, MONOTONE, UNTIE, and LINEAR Transformations SPLINE and MSPLINE Transformations Specifying the Number of Knots SPLINE, BSPLINE, and PSPLINE Comparisons Hypothesis Tests Output Data Set OUTTEST= Output Data Set Computational Resources Unbalanced ANOVA without CLASS Variables Hypothesis Tests for Simple Univariate Models Hypothesis Tests with Monotonicity Constraints Hypothesis Tests with Dependent Variable Transformations Hypothesis Tests with One-Way ANOVA Using the DESIGN Output Option Discrete Choice Experiments: DESIGN, NORESTORE, NOZERO Centering Displayed Output ODS Table Names ODS Graphics -
Examples

- References
| ODS Graphics |
Statistical procedures use ODS Graphics to create graphs as part of their output. ODS Graphics is described in detail in Chapter 21, Statistical Graphics Using ODS.
Before you create graphs, ODS Graphics must be enabled (for example, with the ODS GRAPHICS ON statement). For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21, Statistical Graphics Using ODS.
The overall appearance of graphs is controlled by ODS styles. Styles and other aspects of using ODS Graphics are discussed in the section A Primer on ODS Statistical Graphics in Chapter 21, Statistical Graphics Using ODS.
Some graphs are produced by default; other graphs are produced by using statements and options. You can reference every graph produced through ODS Graphics with a name. The names of the graphs that PROC TRANSREG generates are listed in Table 93.8, along with the required statements and options.
ODS Graph Name |
Plot Description |
Statement & Option |
|---|---|---|
BoxCoxFPlot |
Box-Cox |
MODEL & PROC, BOXCOX transform & PLOTS(UNPACK) |
BoxCoxLogLikePlot |
Box-Cox Log |
MODEL & PROC, BOXCOX transform & PLOTS(UNPACK) |
Box-Cox t or |
MODEL, BOXCOX transform |
|
BoxCoxtPlot |
Box-Cox t |
MODEL & PROC, BOXCOX transform & |
Simple Regression and Separate Group Regressions |
MODEL, a dependent variable that is not transformed, one non-CLASS independent variable, and at most one CLASS variable |
|
Dependent Variable by |
MODEL, PLOTS=OBSERVEDBYPREDICTED |
|
Penalized B-Spline |
MODEL, PBSPLINE transform |
|
Preference Mapping |
MODEL & PROC, IDENTITY transform & COORDINATES |
|
Preference Mapping |
MODEL & PROC, POINT expansion & COORDINATES |
|
Residuals |
PROC, PLOTS=RESIDUALS |
|
RMSEPlot |
Box-Cox Root Mean |
|
ScatterPlot |
Scatter Plot of Observed Data |
MODEL, one non-CLASS independent variable, and at most one CLASS variable, PLOTS=SCATTER |
Variable Transformations |
PROC, PLOTS=TRANSFORMATION |
The PLOTS(INTERPOLATE) Option
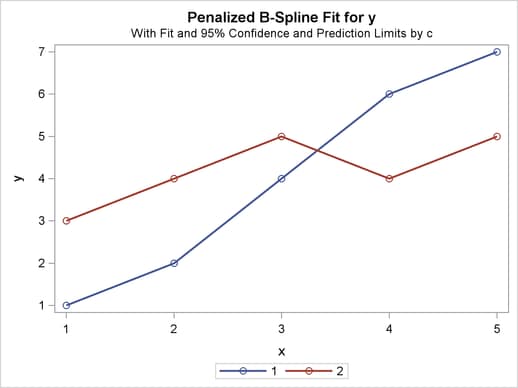
This section illustrates one use of the PLOTS(INTERPOLATE) option for use with ODS Graphics. The data set has two groups of observations, c = 1 and c = 2. Each group is sparse, having only five observations, so the plots of the transformations and fit functions are not smooth. A second DATA step adds additional observations to the data set, over the range of x, with y missing. These observations do not contribute to the analysis, but they are used in computations of transformed and predicted values. The resulting plots are much smoother in the latter case than in the former. The other results of the analysis are the same. The following statements produce Figure 93.77 and Figure 93.78:
title 'Smoother Interpolation with PLOTS(INTERPOLATE)'; data a; input c y x; output; datalines; 1 1 1 1 2 2 1 4 3 1 6 4 1 7 5 2 3 1 2 4 2 2 5 3 2 4 4 2 5 5 ;
ods graphics on;
proc transreg data=a plots=(tran fit) ss2;
model ide(y) = pbs(x) * class(c / zero=none);
run;
data b;
set a end=eof;
output;
if eof then do;
y = .;
do x = 1 to 5 by 0.05;
c = 1; output;
c = 2; output;
end;
end;
run;
proc transreg data=b plots(interpolate)=(tran fit) ss2;
model ide(y) = pbs(x) * class(c / zero=none);
run;
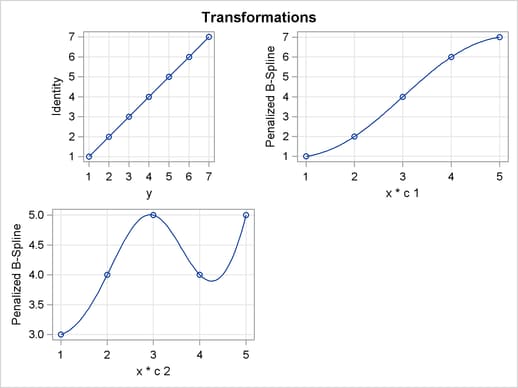
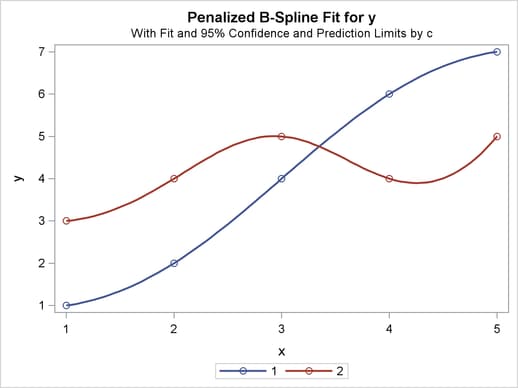
The results with no interpolation are shown in Figure 93.77. The transformation and fit functions are not at all smooth. The results with interpolation are shown in Figure 93.78. The transformation and fit functions are smooth in Figure 93.78, because there are intermediate points to plot.
| Smoother Interpolation with PLOTS(INTERPOLATE) |
| Univariate ANOVA Table, Penalized B-Spline Transformation | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares | Mean Square | F Value | Pr > F |
| Model | 9 | 28.90000 | 3.211111 | Infty | <.0001 |
| Error | 12E-10 | 0.00000 | 0.000000 | ||
| Corrected Total | 9 | 28.90000 | |||
| Root MSE | 0 | R-Square | 1.0000 |
|---|---|---|---|
| Dependent Mean | 4.10000 | Adj R-Sq | 1.0000 |
| Coeff Var | 0 |
| Penalized B-Spline Transformation | |||||
|---|---|---|---|---|---|
| Variable | DF | Coefficient | Lambda | AICC | Label |
| Pbspline(xc1) | 5.0000 | 1.000 | 2.642E-7 | -66.4281 | x * c 1 |
| Pbspline(xc2) | 5.0000 | 1.000 | 2.516E-7 | -60.6430 | x * c 2 |
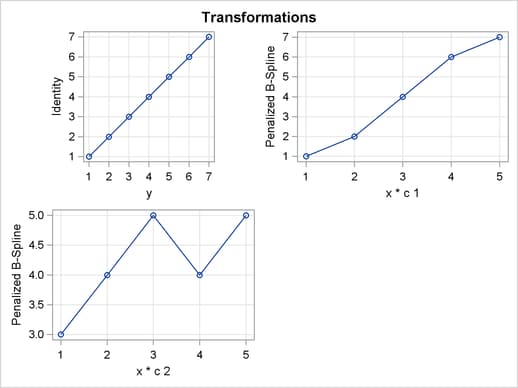
| Smoother Interpolation with PLOTS(INTERPOLATE) |
| Univariate ANOVA Table, Penalized B-Spline Transformation | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares | Mean Square | F Value | Pr > F |
| Model | 9 | 28.90000 | 3.211111 | Infty | <.0001 |
| Error | 12E-10 | 0.00000 | 0.000000 | ||
| Corrected Total | 9 | 28.90000 | |||
| Root MSE | 0 | R-Square | 1.0000 |
|---|---|---|---|
| Dependent Mean | 4.10000 | Adj R-Sq | 1.0000 |
| Coeff Var | 0 |
| Penalized B-Spline Transformation | |||||
|---|---|---|---|---|---|
| Variable | DF | Coefficient | Lambda | AICC | Label |
| Pbspline(xc1) | 5.0000 | 1.000 | 2.642E-7 | -66.4281 | x * c 1 |
| Pbspline(xc2) | 5.0000 | 1.000 | 2.516E-7 | -60.6430 | x * c 2 |