The SURVEYPHREG Procedure
- Overview
- Getting Started
-
Syntax
 PROC SURVEYPHREG Statement BY Statement CLASS Statement CLUSTER Statement DOMAIN Statement ESTIMATE Statement FREQ Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement NLOPTIONS Statement OUTPUT Statement Programming Statements REPWEIGHTS Statement SLICE Statement STORE Statement STRATA Statement TEST Statement WEIGHT Statement
PROC SURVEYPHREG Statement BY Statement CLASS Statement CLUSTER Statement DOMAIN Statement ESTIMATE Statement FREQ Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement NLOPTIONS Statement OUTPUT Statement Programming Statements REPWEIGHTS Statement SLICE Statement STORE Statement STRATA Statement TEST Statement WEIGHT Statement -
Details
 Notation and Estimation Failure Time Distribution Time and CLASS Variables Usage Partial Likelihood Function for the Cox Model Specifying the Sample Design Missing Values Variance Estimation Domain Analysis Hypothesis Tests, Confidence Intervals, and Residuals Output Data Sets Displayed Output ODS Table Names ODS Graphics
Notation and Estimation Failure Time Distribution Time and CLASS Variables Usage Partial Likelihood Function for the Cox Model Specifying the Sample Design Missing Values Variance Estimation Domain Analysis Hypothesis Tests, Confidence Intervals, and Residuals Output Data Sets Displayed Output ODS Table Names ODS Graphics -
Examples

- References
Balanced Repeated Replication (BRR) Method
The balanced repeated replication (BRR) method requires that the full sample be drawn by using a stratified sample design with two primary sampling units (PSUs) per stratum. The BRR method constructs half-sample replicates by deleting one PSU per stratum according to a Hadamard matrix and doubling the original weight of the other PSU in that stratum. Let 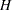 be the total number of strata. The total number of replicates
be the total number of strata. The total number of replicates 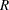 is the smallest multiple of 4 that is greater than
is the smallest multiple of 4 that is greater than 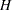 . However, if you prefer a larger number of replicates, you can specify the REPS=n method-option. If a
. However, if you prefer a larger number of replicates, you can specify the REPS=n method-option. If a  Hadamard matrix cannot be constructed, the number of replicates is increased until a Hadamard matrix becomes available.
Hadamard matrix cannot be constructed, the number of replicates is increased until a Hadamard matrix becomes available.
Each replicate is obtained by deleting one PSU per stratum according to a corresponding Hadamard matrix and adjusting the original weights for the remaining PSUs. The new weights are called replicate weights.
Replicates are constructed by using the first 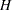 columns of the
columns of the  Hadamard matrix. The
Hadamard matrix. The  th (
th (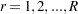 ) replicate is drawn from the full sample according to the
) replicate is drawn from the full sample according to the  th row of the Hadamard matrix as follows:
th row of the Hadamard matrix as follows:
If the
 th element of the Hadamard matrix is
th element of the Hadamard matrix is  , then the first PSU of stratum
, then the first PSU of stratum 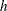 is included in the
is included in the  th replicate and the second PSU of stratum
th replicate and the second PSU of stratum 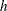 is excluded.
is excluded. If the
 th element of the Hadamard matrix is
th element of the Hadamard matrix is  , then the second PSU of stratum
, then the second PSU of stratum 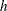 is included in the
is included in the  th replicate and the first PSU of stratum
th replicate and the first PSU of stratum 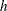 is excluded.
is excluded.
The replicate weights of the remaining PSUs in each half sample are then doubled to their original weights. For more detail about the BRR method, see Wolter (2007) and Lohr (2009).
By default, an appropriate Hadamard matrix is generated automatically to create the replicates. You can display the Hadamard matrix by specifying the VARMETHOD=BRR(PRINTH) method-option. If you provide a Hadamard matrix by specifying the VARMETHOD=BRR(HADAMARD=) method-option, then the replicates are generated according to the provided Hadamard matrix. You can use the VARMETHOD=BRR(OUTWEIGHTS=) method-option to store the replicate weights in a SAS data set.
Let 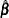 be the estimated proportional hazards regression coefficients from the full sample, and let
be the estimated proportional hazards regression coefficients from the full sample, and let  be the estimated proportional hazards regression coefficients from the
be the estimated proportional hazards regression coefficients from the  th replicate by using replicate weights. PROC SURVEYPHREG estimates the covariance matrix of
th replicate by using replicate weights. PROC SURVEYPHREG estimates the covariance matrix of 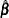 by
by
 |
with 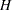 degrees of freedom, where
degrees of freedom, where 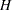 is the number of strata.
is the number of strata.
If one or more components of 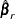 cannot be calculated for some replicates, then the variance estimate is computed by using only the replicates for which the proportional hazards regression coefficients can be estimated. Estimability and nonconvergence are the two most common reasons why
cannot be calculated for some replicates, then the variance estimate is computed by using only the replicates for which the proportional hazards regression coefficients can be estimated. Estimability and nonconvergence are the two most common reasons why 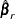 might not be available for a replicate sample even if
might not be available for a replicate sample even if 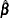 is defined for the full sample. Let
is defined for the full sample. Let  be the number of replicates where
be the number of replicates where 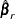 is available and
is available and 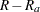 be the number of replicates where
be the number of replicates where 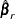 is not available. Without loss of generality, assume that the first
is not available. Without loss of generality, assume that the first  replicates are used; then the BRR variance estimator is
replicates are used; then the BRR variance estimator is
 |
with degrees of freedom equal to the minimum of 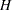 and
and  , where
, where 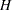 is the number of strata. Alternatively, you can use the FAY= method-option to request Fay’s BRR method, as discussed in the following section.
is the number of strata. Alternatively, you can use the FAY= method-option to request Fay’s BRR method, as discussed in the following section.
Fay’s BRR Method
The traditional BRR method constructs half-sample replicates by deleting one PSU per stratum according to a Hadamard matrix and doubling the original weight of the other PSU. Fay’s BRR method uses the Fay coefficient, 
 , and instead of deleting one PSU per stratum, it multiplies the original weight by the coefficient
, and instead of deleting one PSU per stratum, it multiplies the original weight by the coefficient  . The original weight of the remaining PSU in that stratum is multiplied by
. The original weight of the remaining PSU in that stratum is multiplied by  . PROC SURVEYPHREG uses
. PROC SURVEYPHREG uses 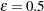 as the default value; alternatively, you can specify a value for
as the default value; alternatively, you can specify a value for  with the FAY= method-option. When
with the FAY= method-option. When  , Fay’s method becomes the traditional BRR method. For more details, see Dippo, Fay, and Morganstein (1984); Fay (1984, 1989); and Judkins (1990). Because the traditional BRR method uses only half of the total sample in every replicate, several replicate estimators (
, Fay’s method becomes the traditional BRR method. For more details, see Dippo, Fay, and Morganstein (1984); Fay (1984, 1989); and Judkins (1990). Because the traditional BRR method uses only half of the total sample in every replicate, several replicate estimators (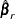 ) might be undefined even when the full sample estimator (
) might be undefined even when the full sample estimator (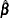 ) is defined. Fay’s BRR method is especially useful for this situation because it uses all the sampled units in every replicate.
) is defined. Fay’s BRR method is especially useful for this situation because it uses all the sampled units in every replicate.
Let 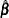 be the estimated proportional hazards regression coefficients from the full sample, and let
be the estimated proportional hazards regression coefficients from the full sample, and let  be the estimated regression coefficients that are obtained from the
be the estimated regression coefficients that are obtained from the  th replicate by using replicate weights. PROC SURVEYPHREG estimates the covariance matrix of
th replicate by using replicate weights. PROC SURVEYPHREG estimates the covariance matrix of 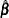 by
by
 |
with 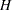 degrees of freedom, where
degrees of freedom, where 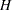 is the number of strata.
is the number of strata.
Hadamard Matrix
PROC SURVEYPHREG uses a Hadamard matrix to construct replicates for BRR variance estimation. You can provide a Hadamard matrix for replicate construction by using the HADAMARD= method-option for VARMETHOD=BRR. Otherwise, PROC SURVEYPHREG generates an appropriate Hadamard matrix. You can display the Hadamard matrix by specifying the PRINTH method-option.
A Hadamard matrix  of dimension
of dimension 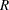 is a square matrix that has all elements equal to 1 or –1 such that
is a square matrix that has all elements equal to 1 or –1 such that 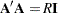 , where
, where 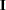 is an identity matrix of appropriate order. The dimension of a Hadamard matrix must equal 1, 2, or a multiple of 4.
is an identity matrix of appropriate order. The dimension of a Hadamard matrix must equal 1, 2, or a multiple of 4.
For example, the following matrix is a Hadamard matrix of dimension  :
:
 |
For BRR replicate construction, the dimension of the Hadamard matrix must be at least 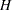 , where
, where 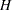 denotes the number of first-stage strata in your design. If a Hadamard matrix of a given dimension exists, it is not necessarily unique. Therefore, if you want to use a specific Hadamard matrix, you must provide the matrix as a SAS data set in the HADAMARD= method-option. You must ensure that the matrix that you provide is actually a Hadamard matrix; PROC SURVEYPHREG does not check the validity of your Hadamard matrix.
denotes the number of first-stage strata in your design. If a Hadamard matrix of a given dimension exists, it is not necessarily unique. Therefore, if you want to use a specific Hadamard matrix, you must provide the matrix as a SAS data set in the HADAMARD= method-option. You must ensure that the matrix that you provide is actually a Hadamard matrix; PROC SURVEYPHREG does not check the validity of your Hadamard matrix.
See the section Balanced Repeated Replication (BRR) Method for details about how the Hadamard matrix is used to construct replicates for BRR variance estimation.