The POWER Procedure
- Overview
-
Getting Started

-
Syntax
 PROC POWER Statement LOGISTIC Statement MULTREG Statement ONECORR Statement ONESAMPLEFREQ Statement ONESAMPLEMEANS Statement ONEWAYANOVA Statement PAIREDFREQ Statement PAIREDMEANS Statement PLOT Statement TWOSAMPLEFREQ Statement TWOSAMPLEMEANS Statement TWOSAMPLESURVIVAL Statement TWOSAMPLEWILCOXON Statement
PROC POWER Statement LOGISTIC Statement MULTREG Statement ONECORR Statement ONESAMPLEFREQ Statement ONESAMPLEMEANS Statement ONEWAYANOVA Statement PAIREDFREQ Statement PAIREDMEANS Statement PLOT Statement TWOSAMPLEFREQ Statement TWOSAMPLEMEANS Statement TWOSAMPLESURVIVAL Statement TWOSAMPLEWILCOXON Statement -
Details
 Overview of Power Concepts Summary of Analyses Specifying Value Lists in Analysis Statements Sample Size Adjustment Options Error and Information Output Displayed Output ODS Table Names Computational Resources Computational Methods and Formulas ODS Graphics ODS Styles Suitable for Use with PROC POWER
Overview of Power Concepts Summary of Analyses Specifying Value Lists in Analysis Statements Sample Size Adjustment Options Error and Information Output Displayed Output ODS Table Names Computational Resources Computational Methods and Formulas ODS Graphics ODS Styles Suitable for Use with PROC POWER -
Examples
 One-Way ANOVA The Sawtooth Power Function in Proportion Analyses Simple AB/BA Crossover Designs Noninferiority Test with Lognormal Data Multiple Regression and Correlation Comparing Two Survival Curves Confidence Interval Precision Customizing Plots Binary Logistic Regression with Independent Predictors Wilcoxon-Mann-Whitney Test
One-Way ANOVA The Sawtooth Power Function in Proportion Analyses Simple AB/BA Crossover Designs Noninferiority Test with Lognormal Data Multiple Regression and Correlation Comparing Two Survival Curves Confidence Interval Precision Customizing Plots Binary Logistic Regression with Independent Predictors Wilcoxon-Mann-Whitney Test - References
Common Notation
Table 70.29 displays notation for some of the more common parameters across analyses. The Associated Syntax column shows examples of relevant analysis statement options, where applicable.
Symbol |
Description |
Associated Syntax |
|---|---|---|
|
Significance level |
ALPHA= |
|
Total sample size |
NTOTAL=, NPAIRS= |
|
Sample size in |
NPERGROUP=, GROUPNS= |
|
Allocation weight for |
GROUPWEIGHTS= |
|
(Arithmetic) mean |
MEAN= |
|
(Arithmetic) mean in |
GROUPMEANS=, PAIREDMEANS= |
|
(Arithmetic) mean difference, |
MEANDIFF= |
|
Null mean or mean difference (arithmetic) |
NULL=, NULLDIFF= |
|
Geometric mean |
MEAN= |
|
Geometric mean in |
GROUPMEANS=, PAIREDMEANS= |
|
Null mean or mean ratio (geometric) |
NULL=, NULLRATIO= |
|
Standard deviation (or common standard deviation per group) |
STDDEV= |
|
Standard deviation in |
GROUPSTDDEVS=, PAIREDSTDDEVS= |
|
Standard deviation of differences |
|
|
Coefficient of variation, defined as the ratio of the standard deviation to the (arithmetic) mean |
CV=, PAIREDCVS= |
|
Correlation |
CORR= |
|
Treatment and reference (arithmetic) means for equivalence test |
GROUPMEANS=, PAIREDMEANS= |
|
Treatment and reference geometric means for equivalence test |
GROUPMEANS=, PAIREDMEANS= |
|
Lower equivalence bound |
LOWER= |
|
Upper equivalence bound |
UPPER= |
|
|
|
|
|
|
|
|
|
|
|
|
|
Binomial distribution with sample size |
A "lower one-sided" test is associated with SIDES=L (or SIDES=1 with the effect smaller than the null value), and an "upper one-sided" test is associated with SIDES=U (or SIDES=1 with the effect larger than the null value).
Owen (1965) defines a function, known as Owen’s 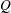 , that is convenient for representing terms in power formulas for confidence intervals and equivalence tests:
, that is convenient for representing terms in power formulas for confidence intervals and equivalence tests:
 |
where  and
and  are the density and cumulative distribution function of the standard normal distribution, respectively.
are the density and cumulative distribution function of the standard normal distribution, respectively.

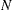
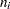
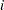 th group
th group 
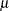

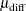
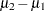 or
or 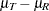






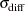
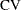
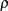




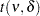
 distribution with d.f.
distribution with d.f.  and noncentrality
and noncentrality 
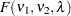
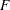 distribution with numerator d.f.
distribution with numerator d.f.  , denominator d.f.
, denominator d.f.  , and noncentrality
, and noncentrality 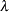

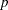 th percentile of
th percentile of 
