The MIANALYZE Procedure
- Overview
- Getting Started
-
Syntax

-
Details

-
Examples
 Reading Means and Standard Errors from Variables in a DATA= Data Set Reading Means and Covariance Matrices from a DATA= COV Data Set Reading Regression Results from a DATA= EST Data Set Reading Mixed Model Results from PARMS= and COVB= Data Sets Reading Generalized Linear Model Results Reading GLM Results from PARMS= and XPXI= Data Sets Reading Logistic Model Results from PARMS= and COVB= Data Sets Reading Mixed Model Results with Classification Variables Using a TEST statement Combining Correlation Coefficients
Reading Means and Standard Errors from Variables in a DATA= Data Set Reading Means and Covariance Matrices from a DATA= COV Data Set Reading Regression Results from a DATA= EST Data Set Reading Mixed Model Results from PARMS= and COVB= Data Sets Reading Generalized Linear Model Results Reading GLM Results from PARMS= and XPXI= Data Sets Reading Logistic Model Results from PARMS= and COVB= Data Sets Reading Mixed Model Results with Classification Variables Using a TEST statement Combining Correlation Coefficients - References
Example 57.9 Using a TEST statement
This example creates an EST-type data set that contains regression coefficients and their corresponding covariance matrices computed from imputed data sets. These estimates are then combined to generate valid statistical inferences about the regression model. A TEST statement is used to test linear hypotheses about the parameters.
The following statements use the REG procedure to generate regression coefficients:
proc reg data=outmi outest=outreg covout noprint; model Oxygen= RunTime RunPulse; by _Imputation_; run;
The following statements combine the results for the imputed data sets. A TEST statement is used to test linear hypotheses of Intercept=0 and RunTime=RunPulse.
proc mianalyze data=outreg edf=28; modeleffects Intercept RunTime RunPulse; test Intercept, RunTime=RunPulse / mult; run;
The "Test Specification" table in Output 57.9.1 displays the 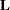 matrix and the
matrix and the  vector in a TEST statement. Since there is no label specified for the TEST statement, "Test 1" is used as the label.
vector in a TEST statement. Since there is no label specified for the TEST statement, "Test 1" is used as the label.
| Test Specification | ||||
|---|---|---|---|---|
| Parameter | L Matrix | C | ||
| Intercept | RunTime | RunPulse | ||
| TestPrm1 | 1.000000 | 0 | 0 | 0 |
| TestPrm2 | 0 | 1.000000 | -1.000000 | 0 |
The "Variance Information" table in Output 57.9.2 displays the between-imputation variance, within-imputation variance, and total variance for each univariate inference. A detailed description of these statistics is provided in the section Combining Inferences from Imputed Data Sets and the section Multiple Imputation Efficiency.
| Variance Information | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | Variance | DF | Relative Increase in Variance |
Fraction Missing Information |
Relative Efficiency |
||
| Between | Within | Total | |||||
| TestPrm1 | 45.529229 | 76.543614 | 131.178689 | 9.1917 | 0.713777 | 0.461277 | 0.915537 |
| TestPrm2 | 0.014715 | 0.114324 | 0.131983 | 20.598 | 0.154459 | 0.141444 | 0.972490 |
The "Parameter Estimates" table in Output 57.9.3 displays the estimated mean and standard error of the linear components. The inferences are based on the t distribution. The table also displays a 95% mean confidence interval and a t test with the associated p-value for the hypothesis that each linear component of 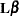 is equal to zero.
is equal to zero.
| Parameter Estimates | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | Estimate | Std Error | 95% Confidence Limits | DF | Minimum | Maximum | C | t for H0: Parameter=C |
Pr > |t| | |
| TestPrm1 | 90.837440 | 11.453327 | 65.01034 | 116.6645 | 9.1917 | 83.020730 | 100.839807 | 0 | 7.93 | <.0001 |
| TestPrm2 | -2.964292 | 0.363294 | -3.72070 | -2.2079 | 20.598 | -3.091586 | -2.763582 | 0 | -8.16 | <.0001 |
With the MULT option, the procedure assumes that the between-imputation covariance matrix is proportional to the within-imputation covariance matrix and displays a multivariate inference for all the linear components taken jointly in Output 57.9.4.
| Multivariate Inference Assuming Proportionality of Between/Within Covariance Matrices |
||||
|---|---|---|---|---|
| Avg Relative Increase in Variance |
Num DF | Den DF | F for H0: Parameter=Theta0 |
Pr > F |
| 0.419868 | 2 | 35.053 | 60.34 | <.0001 |