Path Diagrams and Path Analysis
Sections Errors-in-Variables Regression, Regression with Measurement Errors in 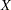 and
and 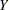 , and Illustration of Model Identification: Spleen Data show how you can specify models by means of equations in the LINEQS modeling language. This section shows you how to specify models that are represented by path diagrams. The PATH modeling language of PROC CALIS is the main tool for this purpose.
, and Illustration of Model Identification: Spleen Data show how you can specify models by means of equations in the LINEQS modeling language. This section shows you how to specify models that are represented by path diagrams. The PATH modeling language of PROC CALIS is the main tool for this purpose.
Complicated models are often easier to understand when they are expressed as path diagrams. One advantage of path diagrams over equations is that variances and covariances can be shown directly in the path diagram. Loehlin (1987) provides a detailed discussion of path diagrams. Another advantage is that the path diagram can be transcribed easily into the PATH modeling language supported by PROC CALIS.
A path diagram for the spleen data is shown in Figure 17.13. It explicitly shows all latent variables (including error terms) and variances of exogenous variables.

The path diagram shown in Figure 17.13 is essentially a graphical representation of the same just-identified model for the spleen data that is described in the section Illustration of Model Identification: Spleen Data. In path diagrams, it is customary to write the names of manifest or observed variables in rectangles and the names of latent variables in ovals. For example, sqrtrose and sqrtnucl are observed variables in the path diagram, while all others are latent variables.
The effects (the regression coefficients) in each equation are indicated by drawing arrows from the predictor variables to the outcome variable. For example, the path from factnucl to factrose is labeled with the regression coefficient beta in the path diagram shown in Figure 17.13. Other paths are labeled with fixed coefficients (or effects) of 1.
Variances of exogenous variables are drawn as double-headed arrows in Figure 17.13. For example, the variance of disturb is shown as a double-headed arrow pointing to the variable itself and is named v_disturb. Variances of the err_nucl and err_rose are also drawn as double-headed arrows but are labeled with fixed constants 0.25.
The path diagram shown in Figure 17.13 matches the features in the LINEQS model closely. For example, the error terms are depicted explicitly and their paths (regression coefficients) that connect to the associated endogenous variables are marked with fixed constants 1, reflecting the same specification in the equations of the LINEQS model. However, you can simplify the path diagram by using McArdle’s RAM (reticular action model) notation (McArdle and McDonald; 1984), as described in the following section.
A Simplified Path Diagram for the Spleen Data
The main simplification in the path diagram is to drop all the error terms in the model. Instead, error variances are treated as residual (or partial) variances for the endogenous variables in the model or path diagram. Hence, in the path diagrams for RAM models, error variances are also represented by double-headed arrows directly attached to the endogenous variables, which is the same way you represent variances for the exogenous variables. The RAM model convention leads to a simplified representation of the path diagram for the spleen data, as shown in Figure 17.14.

Another simplification done in Figure 17.14 is the omission of the parameter labeling in the path diagram. This simplification is not a part of the RAM notation. It is just a convention in PROC CALIS that you can omit the unconstrained parameter names without affecting the meaning of the model. Hence, the parameter names beta, v_disturb, and v_factnucl are no longer necessary in the simplified path diagram Figure 17.14. As you can see, this convention makes the task of model specification considerably simpler and easier.
The following statements show the specification of the simplified path diagram in Figure 17.14:
proc calis data=spleen;
path
sqrtrose <--- factrose = 1.0,
sqrtnucl <--- factnucl = 1.0,
factrose <--- factnucl ;
pvar
sqrtrose = 0.25, /* error variance for sqrtrose */
sqrtnucl = 0.25, /* error variance for sqrtnucl */
factrose, /* disturbance/error variance for factrose */
factnucl; /* variance of factnucl */
run;
The PATH statement invokes the PATH modeling language of PROC CALIS. In the PATH modeling language, each entry of specification corresponds to either a single- or double- headed arrow specification in the path diagram shown in Figure 17.14, as explained in the following:
The PATH statement enables you to specify each of the single-headed arrows (paths) as path entries, which are separated by commas. You have three single-headed arrows in the path diagram and therefore you have three path entries in the PATH statement. The path entries "sqrtrose <--- factrose" and "sqrtnucl <--- factnucl" are followed by the constant 1, indicating fixed path coefficients. The path "factrose <--- factnucl" is also specified, but without giving a fixed value or a parameter name. By default, this path entry is associated with a free parameter for the effect or path coefficient.
The PVAR statement enables you to specify each of the double-headed arrows with both heads pointing to the same variable, exogenous or endogenous. This type of arrows represents variances or error variances. You have four such double-headed arrows in the path diagram, and therefore there are four corresponding entries under the PVAR statement. Two of them are assigned with fixed constants (0.25), and the remaining two (error variance of factrose and variance of factnucl) are free variance parameters.
The PCOV statement enables you to specify each of the double-headed arrows with its heads pointing to different variables, exogenous or endogenous. This type of arrows represents covariances between variables or their error terms. You do not have this type of double-headed arrows in the current path diagram, and therefore you do not need a PCOV statement for the corresponding model specification.
The estimation results are shown in Figure 17.15. Essentially, these are exactly the same estimation results as those that result from the LINEQS modeling language for the just-identified model in section Illustration of Model Identification: Spleen Data.
| PATH List | ||||||
|---|---|---|---|---|---|---|
| Path | Parameter | Estimate | Standard Error |
t Value | ||
| sqrtrose | <--- | factrose | 1.00000 | |||
| sqrtnucl | <--- | factnucl | 1.00000 | |||
| factrose | <--- | factnucl | _Parm1 | 0.39074 | 0.07708 | 5.06920 |
| Variance Parameters | |||||
|---|---|---|---|---|---|
| Variance Type |
Variable | Parameter | Estimate | Standard Error |
t Value |
| Error | sqrtrose | 0.25000 | |||
| sqrtnucl | 0.25000 | ||||
| factrose | _Parm2 | 0.38153 | 0.28556 | 1.33607 | |
| Exogenous | factnucl | _Parm3 | 10.50458 | 4.58577 | 2.29069 |
Notice in Figure 17.15 that the path coefficient for path "factrose <--- factnucl" is given a parameter name _Parm1, which is generated automatically by PROC CALIS. This is the same beta parameter of the LINEQS model in the section Illustration of Model Identification: Spleen Data. Also, the variance parameters _Parm2 and _Parm3 in Figure 17.15 are the same v_disturb and v_factnucl parameters, respectively, in the preceding LINEQS model.
In PROC CALIS, using parameter names to specify free parameters is optional. Parameter names are generated for free parameters by default. Or, if you choose parameter names for your own convenience, you can do so without changing the model specification. For example, you can specify the preceding PATH model equivalently by adding the desired parameter names, as shown in the following statements:
proc calis data=spleen;
path
sqrtrose <--- factrose = 1.0,
sqrtnucl <--- factnucl = 1.0,
factrose <--- factnucl = beta;
pvar
sqrtrose = 0.25, /* error variance for sqrtrose */
sqrtnucl = 0.25, /* error variance for sqrtnucl */
factrose = v_disturb, /* disturbance/error variance for factrose */
factnucl = v_factnucl; /* variance of factnucl */
run;
A path diagram provides you an easy and conceptual way to represent your model, while the PATH modeling language in PROC CALIS offers you an easy way to input your path diagram in a non-graphical fashion. This is especially useful for models with more complicated path structures. See the section A Combined Measurement-Structural Model for a more elaborated example of the PATH model application.
The next section provides examples of the PATH model applied to classical test theory.