Example 24.3 Split Plot
In some experiments, treatments can be applied only to groups of experimental observations rather than separately to each observation. When there are two nested groupings of the observations on the basis of treatment application, this is known as a split plot design. For example, in integrated circuit fabrication it is of interest to see how different manufacturing methods affect the characteristics of individual chips. However, much of the manufacturing process is applied to a relatively large wafer of material, from which many chips are made. Additionally, a chip’s position within a wafer might also affect chip performance. These two groupings of chips—by wafer and by position-within-wafer—might form the whole plots and the subplots, respectively, of a split plot design for integrated circuits.
The following statements produce an analysis for a split-plot design. The CLASS statement includes the variables Block, A, and B, where B defines subplots within BLOCK*A whole plots. The MODEL statement includes the independent effects Block, A, Block*A, B, and A*B. The TEST statement asks for an 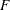 test of the A effect that uses the Block*A effect as the error term. The following statements produce Output 24.3.1 and Output 24.3.2:
test of the A effect that uses the Block*A effect as the error term. The following statements produce Output 24.3.1 and Output 24.3.2:
title1 'Split Plot Design';
data Split;
input Block 1 A 2 B 3 Response;
datalines;
142 40.0
141 39.5
112 37.9
111 35.4
121 36.7
122 38.2
132 36.4
131 34.8
221 42.7
222 41.6
212 40.3
211 41.6
241 44.5
242 47.6
231 43.6
232 42.8
;
proc anova data=Split;
class Block A B;
model Response = Block A Block*A B A*B;
test h=A e=Block*A;
run;
Output 24.3.1
Class Level Information and ANOVA Table
The ANOVA Procedure
Dependent Variable: Response
| 11 |
182.0200000 |
16.5472727 |
7.85 |
0.0306 |
| 4 |
8.4300000 |
2.1075000 |
|
|
| 15 |
190.4500000 |
|
|
|
| 0.955736 |
3.609007 |
1.451723 |
40.22500 |
First, notice that the overall 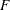 test for the model is significant.
test for the model is significant.
Output 24.3.2
Tests of Effects
| 1 |
131.1025000 |
131.1025000 |
62.21 |
0.0014 |
| 3 |
40.1900000 |
13.3966667 |
6.36 |
0.0530 |
| 3 |
6.9275000 |
2.3091667 |
1.10 |
0.4476 |
| 1 |
2.2500000 |
2.2500000 |
1.07 |
0.3599 |
| 3 |
1.5500000 |
0.5166667 |
0.25 |
0.8612 |
| 3 |
40.19000000 |
13.39666667 |
5.80 |
0.0914 |
The effect of Block is significant. The effect of A is not significant: look at the 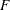 test produced by the TEST statement, not at the
test produced by the TEST statement, not at the 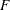 test produced by default. Neither the B nor A*B effects are significant. The test for Block*A is irrelevant, as this is simply the main-plot error.
test produced by default. Neither the B nor A*B effects are significant. The test for Block*A is irrelevant, as this is simply the main-plot error.
Copyright © SAS Institute Inc. All rights reserved.
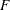 test of the A effect that uses the Block*A effect as the error term. The following statements produce Output 24.3.1 and Output 24.3.2:
test of the A effect that uses the Block*A effect as the error term. The following statements produce Output 24.3.1 and Output 24.3.2: 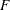 test for the model is significant.
test for the model is significant. 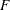 test produced by the TEST statement, not at the
test produced by the TEST statement, not at the 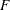 test produced by default. Neither the B nor A*B effects are significant. The test for Block*A is irrelevant, as this is simply the main-plot error.
test produced by default. Neither the B nor A*B effects are significant. The test for Block*A is irrelevant, as this is simply the main-plot error. 