The ANOVA Procedure
Example 24.1 Randomized Complete Block With Factorial Treatment Structure
This example uses statements for the analysis of a randomized block with two treatment factors occurring in a factorial structure. The data, from Neter, Wasserman, and Kutner (1990, p. 941), are from an experiment examining the effects of codeine and acupuncture on post-operative dental pain in male subjects. Both treatment factors have two levels. The codeine levels are a codeine capsule or a sugar capsule. The acupuncture levels are two inactive acupuncture points or two active acupuncture points. There are four distinct treatment combinations due to the factorial treatment structure. The 32 subjects are assigned to eight blocks of four subjects each based on an assessment of pain tolerance.
The data for the analysis are balanced, so PROC ANOVA is used. The data are as follows:
title1 'Randomized Complete Block With Two Factors'; data PainRelief; input PainLevel Codeine Acupuncture Relief @@; datalines; 1 1 1 0.0 1 2 1 0.5 1 1 2 0.6 1 2 2 1.2 2 1 1 0.3 2 2 1 0.6 2 1 2 0.7 2 2 2 1.3 3 1 1 0.4 3 2 1 0.8 3 1 2 0.8 3 2 2 1.6 4 1 1 0.4 4 2 1 0.7 4 1 2 0.9 4 2 2 1.5 5 1 1 0.6 5 2 1 1.0 5 1 2 1.5 5 2 2 1.9 6 1 1 0.9 6 2 1 1.4 6 1 2 1.6 6 2 2 2.3 7 1 1 1.0 7 2 1 1.8 7 1 2 1.7 7 2 2 2.1 8 1 1 1.2 8 2 1 1.7 8 1 2 1.6 8 2 2 2.4 ;
The variable PainLevel is the blocking variable, and Codeine and Acupuncture represent the levels of the two treatment factors. The variable Relief is the pain relief score (the higher the score, the more relief the patient has).
The following statements invokes PROC ANOVA. The blocking variable and treatment factors appear in the CLASS statement. The bar between the treatment factors Codeine and Acupuncture adds their main effects as well as their interaction Codeine*Acupuncture to the model.
proc anova data=PainRelief; class PainLevel Codeine Acupuncture; model Relief = PainLevel Codeine|Acupuncture; run;
The results from the analysis are shown in Output 24.1.1, Output 24.1.2, and Output 24.1.3.
| Randomized Complete Block With Two Factors |
| Class Level Information | ||
|---|---|---|
| Class | Levels | Values |
| PainLevel | 8 | 1 2 3 4 5 6 7 8 |
| Codeine | 2 | 1 2 |
| Acupuncture | 2 | 1 2 |
| Number of Observations Read | 32 |
|---|---|
| Number of Observations Used | 32 |
| Randomized Complete Block With Two Factors |
| Source | DF | Sum of Squares | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Model | 10 | 11.33500000 | 1.13350000 | 78.37 | <.0001 |
| Error | 21 | 0.30375000 | 0.01446429 | ||
| Corrected Total | 31 | 11.63875000 |
| R-Square | Coeff Var | Root MSE | Relief Mean |
|---|---|---|---|
| 0.973902 | 10.40152 | 0.120268 | 1.156250 |
The Class Level Information and ANOVA table are shown in Output 24.1.1 and Output 24.1.2. The classification level information summarizes the structure of the design. It is good to check these consistently in search of errors in the DATA step. The overall 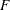 test is significant, indicating that the model accounts for a significant amount of variation in the dependent variable.
test is significant, indicating that the model accounts for a significant amount of variation in the dependent variable.
| Source | DF | Anova SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| PainLevel | 7 | 5.59875000 | 0.79982143 | 55.30 | <.0001 |
| Codeine | 1 | 2.31125000 | 2.31125000 | 159.79 | <.0001 |
| Acupuncture | 1 | 3.38000000 | 3.38000000 | 233.68 | <.0001 |
| Codeine*Acupuncture | 1 | 0.04500000 | 0.04500000 | 3.11 | 0.0923 |
Output 24.1.3 shows tests of the effects. The blocking effect is significant; hence, it is useful. The interaction between codeine and acupuncture is significant at the 90% level but not at the 95% level. The significance level of this test should be determined before the analysis. The main effects of both treatment factors are highly significant.
