| Shared Concepts and Topics |
| Syntax: ESTIMATE Statement |
- ESTIMATE <'label'> estimate-specification <(divisor=n)>
<, <'label'> estimate-specification <(divisor=n)> > <, ...>
< / options> ;
The basic element of the ESTIMATE statement is the estimate-specification, which consists of model effects and their coefficients. A estimate-specification takes the general form
The following variables can appear in the ESTIMATE statement:
- label
is an optional label that identifies the particular row of the estimate in the output.
- effect
identifies an effect that appears in the MODEL statement. The keyword INTERCEPT can be used as an effect when an intercept is fitted in the model. You do not need to include all effects that are in the MODEL statement.
- values
are constants that are elements of the
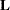 matrix and are associated with the fixed and random effects. There are two basic methods of specifying the entries of the
matrix and are associated with the fixed and random effects. There are two basic methods of specifying the entries of the 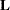 matrix. The traditional representation—also known as the positional syntax—relies on entering coefficients in the position they assume in the
matrix. The traditional representation—also known as the positional syntax—relies on entering coefficients in the position they assume in the 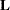 matrix. For example, in the following statements the elements of
matrix. For example, in the following statements the elements of 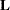 that are associated with the b main effect receive a
that are associated with the b main effect receive a  in the first position and a
in the first position and a 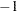 in the second position:
in the second position: class a b; model y = a b a*b; estimate 'B at A2' b 1 -1 a*b 0 0 1 -1;
The elements that are associated with the interaction receive a
 in the third position and a
in the third position and a 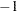 in the fourth position. In order to specify coefficients correctly for the interaction term, you need to know how the levels of a and b vary in the interaction, which is governed by the order of the variables in the CLASS statement. The nonpositional syntax is designed to make it easier to enter coefficients for interactions and is necessary to enter coefficients for effects that are constructed with the EFFECT statement. In square brackets you enter the coefficient followed by the associated levels of the CLASS variables. If B has two levels and A has three levels, the previous ESTIMATE statement, by using nonpositional syntax for the interaction term, becomes the following statement:
in the fourth position. In order to specify coefficients correctly for the interaction term, you need to know how the levels of a and b vary in the interaction, which is governed by the order of the variables in the CLASS statement. The nonpositional syntax is designed to make it easier to enter coefficients for interactions and is necessary to enter coefficients for effects that are constructed with the EFFECT statement. In square brackets you enter the coefficient followed by the associated levels of the CLASS variables. If B has two levels and A has three levels, the previous ESTIMATE statement, by using nonpositional syntax for the interaction term, becomes the following statement: estimate 'B at A2' b 1 -1 a*b [1, 2 1] [-1, 2 2];
The previous statement assigns value
 to the interaction where A is at level 2 and B is at level 1, and it assigns
to the interaction where A is at level 2 and B is at level 1, and it assigns 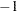 to the interaction where both classification variables are at level 2. The comma that separates the entry for the
to the interaction where both classification variables are at level 2. The comma that separates the entry for the 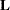 matrix from the level indicators is optional. Further details about the nonpositional contrast syntax and its use with constructed effects can be found in the section Positional and Nonpositional Syntax for Coefficients in Linear Functions.
matrix from the level indicators is optional. Further details about the nonpositional contrast syntax and its use with constructed effects can be found in the section Positional and Nonpositional Syntax for Coefficients in Linear Functions.
Based on the estimate-specifications in your ESTIMATE statement, the procedure constructs the matrix 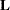 to test the hypothesis
to test the hypothesis  . The procedure supports nonpositional syntax for the coefficients of model effects in the ESTIMATE statement. For details see the section Positional and Nonpositional Syntax for Coefficients in Linear Functions.
. The procedure supports nonpositional syntax for the coefficients of model effects in the ESTIMATE statement. For details see the section Positional and Nonpositional Syntax for Coefficients in Linear Functions.
The procedure then produces for each row  of
of 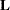 an approximate t test of the hypothesis
an approximate t test of the hypothesis  . You can also obtain multiplicity-adjusted p-values and confidence limits for multirow estimates with the ADJUST= option.
. You can also obtain multiplicity-adjusted p-values and confidence limits for multirow estimates with the ADJUST= option.
Note that multirow estimates are permitted. Unlike releases prior to SAS 9.22, you do not need to specify a 'label' for every row of the estimate; the procedure constructs a default label if a label is not specified.
If the procedure finds the estimate to be nonestimable, then it displays "Non-est" for the estimate entry.
Table 19.17 summarizes important options in the ESTIMATE statement. All ESTIMATE options are subsequently discussed in alphabetical order.
Option |
Description |
|---|---|
Construction and Computation of Estimable Functions |
|
Specifies a list of values to divide the coefficients |
|
Suppresses the automatic fill-in of coefficients for higher-order effects |
|
Tunes the estimability checking difference |
|
Degrees of Freedom and p-values |
|
Determines the method for multiple comparison adjustment of estimates |
|
Determines the confidence level ( |
|
Performs one-sided, lower-tailed inference |
|
Adjusts multiplicity-corrected p-values further in a step-down fashion |
|
Specifies values under the null hypothesis for tests |
|
Performs one-sided, upper-tailed inference |
|
Statistical Output |
|
Constructs confidence limits |
|
Displays the correlation matrix of estimates |
|
Displays the covariance matrix of estimates |
|
Prints the |
|
Produces a joint |
|
Requests ODS statistical graphics if the analysis is sampling-based |
|
Specifies the seed for computations that depend on random numbers |
|
Generalized Linear Modeling |
|
Specifies how to construct estimable functions with multinomial data |
|
Exponentiates and displays estimates |
|
Computes and displays estimates and standard errors on the inverse linked scale |
|
You can specify the following options in the ESTIMATE statement after a slash (/).
- ADJDFE=SOURCE
- ADJDFE=ROW
specifies how denominator degrees of freedom are determined when p-values and confidence limits are adjusted for multiple comparisons with the ADJUST= option. When you do not specify the ADJDFE= option, or when you specify ADJDFE=SOURCE, the denominator degrees of freedom for multiplicity-adjusted results are the denominator degrees of freedom for the final effect that is listed in the ESTIMATE statement from the "Type III" table.
The ADJDFE=ROW setting is useful if you want multiplicity adjustments to take into account that denominator degrees of freedom are not constant across estimates. For example, this can be the case when the denominator degrees of freedom are computed by the Satterthwaite method or according to Kenward and Roger (1997).
The ADJDFE= option has an effect only in mixed models that use these degree-of-freedom methods. It is not supported by the procedures that perform chi-square-based inference (LOGISTIC, PHREG, and SURVEYLOGISTIC).
- ADJUST=BON
- ADJUST=SCHEFFE
- ADJUST=SIDAK
- ADJUST=SIMULATE<(simoptions)>
- ADJUST=T
requests a multiple comparison adjustment for the p-values and confidence limits for the estimates. The adjusted quantities are produced in addition to the unadjusted quantities. Adjusted confidence limits are produced if the CL or ALPHA= option is in effect. For a description of the adjustments, see Chapter 39, The GLM Procedure, and Chapter 58, The MULTTEST Procedure, and the documentation for the ADJUST= option in the LSMEANS statement.
If the STEPDOWN option is in effect, the p-values are further adjusted in a step-down fashion.
- ALPHA=number
requests that a t type confidence interval be constructed with confidence level
 . The value of number must be between 0 and 1; the default is 0.05. If the "Estimates" table shows infinite degrees of freedom, then the confidence interval is a z type interval.
. The value of number must be between 0 and 1; the default is 0.05. If the "Estimates" table shows infinite degrees of freedom, then the confidence interval is a z type interval. - CATEGORY=category-options
specifies how to construct estimates and multiplicity corrections for models with multinomial data (ordinal or nominal). This option is also important for constructing sets of estimable functions for F or chi-square tests with the JOINT option.
The category-options are used to indicate how response variable levels are treated in constructing the estimable functions. Possible values for the category-options are the following:- JOINT
computes the estimable functions for every nonredundant category and treats them as a set. For example, a three-row ESTIMATE statement in a model with three response categories leads to six estimable functions.
- SEPARATE
computes the estimable functions for every nonredundant category in turn. For example, a three-row ESTIMATE statement in a model with three response categories leads to two sets of three estimable functions.
- quoted-value-list
computes the estimable functions only for the list of values given. The list must consist of formatted values of the response categories.
Consider the following ESTIMATE statements in the LOGISTIC procedure for an ordinal model with response categories 'vg', 'g', 'm', 'b', and 'vb'. Because there are five response categories, there are four nonredundant categories for the cumulative link model.
proc logistic data=icecream; class brand / param=glm; model taste(order=data) = brand / link=logit; freq count; estimate brand 1 -1, intercept 1 brand 0 1 / category='m','vg'; estimate intercept 1 brand 1 / category=joint adjust=simulate(seed=1); estimate brand 1 -1, brand 1 1 -2 / category=separate adjust=bon; run;The first ESTIMATE statement requests a two-row estimable function. The result is produced for two of the four nonredundant response categories. The second ESTIMATE statement produces four t tests, one for each nonredundant category. The multiplicity adjustment with p-value computation by simulation treats the four estimable functions as a unit for family-wise Type I error protection. The third ESTIMATE statement computes a two-row estimable function and reports its results separately for all nonredundant categories. The Bonferroni adjustment in this statement applies to a family of two tests that correspond to the two-row estimable function. Four Bonferroni adjustments for sets of size two are performed.
The CATEGORY= option is supported only by the procedures that support generalized linear modeling (LOGISTIC and SURVEYLOGISTIC) and by PROC PLM when it is used to perform statistical analyses on item stores created by these procedures.
- CHISQ
requests that chi-square tests be performed in addition to F tests, when you request an F test with the JOINT option. This option has no effect in procedures that produce chi-square statistics by default.
- CL
requests that t type confidence limits be constructed. If the procedure shows the degrees of freedom in the "Estimates" table as infinite, then the confidence limits are z intervals. The confidence level is 0.95 by default, and you can change the confidence level with the ALPHA= option. The confidence intervals are adjusted for multiplicity when you specify the ADJUST= option. However, if a step-down p-value adjustment is requested with the STEPDOWN option, only the p-values are adjusted for multiplicity.
- CORR
displays the estimated correlation matrix of the linear combination of the parameter estimates.
- COV
displays the estimated covariance matrix of the linear combination of the parameter estimates.
- DF=number
specifies the degrees of freedom for the t test and confidence limits. This option is not supported by the procedures that perform chi-square-based inference (LOGISTIC, PHREG, and SUVEYLOGISTIC).
- DIVISOR=value-list
specifies a list of values by which to divide the coefficients so that fractional coefficients can be entered as integer numerators. If you do not specify value-list, a default value of 1.0 is assumed. Missing values in the value-list are converted to 1.0.
If the number of elements in value-list exceeds the number of rows of the estimate, the extra values are ignored. If the number of elements in value-list is less than the number of rows of the estimate, the last value in value-list is copied forward.
If you specify a row-specific divisor as part of the specification of the estimate row, this value multiplies the corresponding divisor that is implied by the value-list. For example, the following statement divides the coefficients in the first row by 8, and the coefficients in the third and fourth row by 3:
estimate 'One vs. two' A 2 -2 (divisor=2), 'One vs. three' A 1 0 -1 , 'One vs. four' A 3 0 0 -3 , 'One vs. five' A 1 0 0 0 -1 / divisor=4,.,3;Coefficients in the second row are not altered.
- E
- EXP
requests exponentiation of the estimate. When you model data with the logit, cumulative logit, or generalized logit link functions, and the estimate represents a log odds ratio or log cumulative odds ratio, the EXP option produces an odds ratio. In proportional hazards model, this option produces estimates of hazard ratios. If you specify the CL or ALPHA= option, the (adjusted) confidence bounds are also exponentiated.
The EXP option is supported only by PROC PHREG, PROC SURVEYPHREG, the procedures that support generalized linear modeling (LOGISTIC and SURVEYLOGISTIC), and by PROC PLM when it is used to perform statistical analyses on item stores created by these procedures.
- ILINK
requests that the estimate and its standard error also be reported on the scale of the mean (the inverse linked scale). The computation of the inverse linked estimate depends on the estimation mode. For example, if the analysis is based on a posterior sample when a BAYES statement is present, the inversely linked estimate is the average of the inversely linked values across the sample of posterior parameter estimates. If the analysis is not based on a sample of parameter estimates, the procedure computes the value on the mean scale by applying the inverse link to the estimate.
The interpretation of this quantity depends on the effect values specified in your ESTIMATE statement and on the link function. For example, in a model for binary data with logit link the following statements compute
where
 and
and 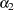 are the fixed-effects solutions that are associated with the first two levels of the classification effect A:
are the fixed-effects solutions that are associated with the first two levels of the classification effect A: class A; model y = A / dist=binary link=logit; estimate 'A one vs. two' A 1 -1 / ilink;
This quantity is not the difference of the probabilities that are associated with the two levels,

The standard error of the inversely linked estimate is based on the delta method. If you also specify the CL option, the procedure computes confidence limits for the estimate on the mean scale. In multinomial models for nominal data, the limits are obtained by the delta method. In other models they are obtained from the inverse link transformation of the confidence limits for the estimate. The ILINK option is specific to an ESTIMATE statement.
The ILINK option is supported only by the procedures that support generalized linear modeling (LOGISTIC and SURVEYLOGISTIC) and by PROC PLM when it is used to perform statistical analyses on item stores created by these procedures.
- JOINT<(joint-test-options)>
requests that a joint F or chi-square test be produced for the rows of the estimate. The JOINT option in the ESTIMATE statement essentially replaces the CONTRAST statement.
When the LOWERTAILED or the UPPERTAILED options are in effect, or if the BOUNDS option described below is in effect, the JOINT option produces the chi-bar-square statistic according to Silvapulle and Sen (2004). This statistic uses a simulation-based approach to compute p-values in situations where the alternative hypotheses of the estimable functions are not simple two-sided hypotheses. See the section Joint Hypothesis Tests with Complex Alternatives, the Chi-Bar-Square Statistic for more information about this test statistic.
You can specify the following joint-test-options in parentheses:
-
ACC=

specifies the accuracy radius for determining the necessary sample size in the simulation-based approach of Silvapulle and Sen (2004) for tests with order restrictions. The value of
 must be strictly between 0 and 1; the default value is 0.005.
must be strictly between 0 and 1; the default value is 0.005. -
EPS=

specifies the accuracy confidence level for determining the necessary sample size in the simulation-based approach of Silvapulle and Sen (2004) for tests with order restrictions. The value of
 must be strictly between 0 and 1; the default value is 0.01.
must be strictly between 0 and 1; the default value is 0.01. - LABEL='label'
assigns an identifying label to the joint test. If you do not specify a label, the first non-default label for the ESTIMATE rows is used to label the joint test.
- NOEST
- ONLY
performs only the F or chi-square test and suppresses other results from the ESTIMATE statement. This option is useful for emulating the CONTRAST statement that is available in other procedures.
- NSAMP=n
specifies the number of samples for the simulation-based method of Silvapulle and Sen (2004). If n is not specified, it is constructed from the values of the ALPHA=
 , the ACC=
, the ACC= , and the EPS=
, and the EPS= options. With the default values for
options. With the default values for  ,
,  , and
, and  (0.005, 0.01, and 0.05, respectively), NSAMP=12,604 by default.
(0.005, 0.01, and 0.05, respectively), NSAMP=12,604 by default. - CHISQ
adds a chi-square test if the procedure produces an F test by default.
- BOUNDS=value-list
specifies boundary values for the estimable linear function. The null value of the hypothesis is always zero. If you specify a positive boundary value
 , the hypotheses are
, the hypotheses are 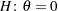 ,
,  with the added constraint that
with the added constraint that 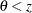 . The same is true for negative boundary values. The alternative hypothesis is then
. The same is true for negative boundary values. The alternative hypothesis is then 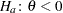 subject to the constraint
subject to the constraint  . If you specify a missing value, the hypothesis is assumed to be two-sided. The BOUNDS option enables you to specify sets of one- and two-sided joint hypotheses. If all values in value-list are set to missing, the procedure performs a simulation-based p-value calculation for a two-sided test.
. If you specify a missing value, the hypothesis is assumed to be two-sided. The BOUNDS option enables you to specify sets of one- and two-sided joint hypotheses. If all values in value-list are set to missing, the procedure performs a simulation-based p-value calculation for a two-sided test.
-
ACC=
- LOWER
- LOWERTAILED
requests that the p-value for the t test be based only on values that are less than the test statistic. A two-tailed test is the default. A lower-tailed confidence limit is also produced if you specify the CL or ALPHA= option.
Note that for ADJUST=SCHEFFE the one-sided adjusted confidence intervals and one-sided adjusted p-values are the same as the corresponding two-sided statistics, because this adjustment is based on only the right tail of the
 distribution.
distribution. If you request a joint test with the JOINT option, then a one-sided left-tailed order restriction is applied to all estimable functions, and the corresponding chi-bar-square statistic of Silvapulle and Sen (2004) is computed in addition to the two-sided, standard, F or chi-square statistic. See the JOINT option for how to control the computation of the simulation-based chi-bar-square statistic.
- NOFILL
suppresses the automatic fill-in of coefficients of higher-order effects.
- PLOTS=plot-options
produces ODS statistical graphics of the distribution of estimable functions if the procedure performs the analysis in a sampling-based mode. For example, this is the case when procedures support a BAYES statement and perform a Bayesian analysis. The estimable functions are then computed for each of the posterior parameter estimates, and the "Estimates" table reports simple descriptive statistics for the evaluated functions. The PLOTS= option enables you in this situation to visualize the distribution of the estimable function. The following plot-options are available:
- ALL
produces all possible plots with their default settings.
- BOXPLOT<(boxplot-options)>
produces box plots of the distribution of the estimable function across the posterior sample. A separate box is generated for each estimable function, and all boxes appear on a single graph by default. You can affect the appearance of the box plot graph with the following options:
- ORIENTATION=VERTICAL
 |
| HORIZONTAL
HORIZONTAL - ORIENT=VERT
 |
| HORIZ
HORIZ specifies the orientation of the boxes. The default is vertical orientation of the box plots.
- NPANELPOS=number
specifies how to break the series of box plots across multiple panels. If the NPANELPOS option is not specified, or if number equals zero, then all box plots are displayed in a single graph; this is the default. If a negative number is specified, then exactly up to
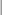 number
number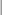 of box plots are displayed per panel. If number is positive, then the number of boxes per panel is balanced to achieve small variation in the number of box plots per graph.
of box plots are displayed per panel. If number is positive, then the number of boxes per panel is balanced to achieve small variation in the number of box plots per graph.
- ORIENTATION=VERTICAL
- DISTPLOT<(distplot-options)>
- DIST<(distplot-options)>
generates panels of histograms with a kernel density overlaid. A separate plot in each panel contains the results for each estimable function. You can specify the following distplot-options in parentheses:
- BOX
 |
| NOBOX
NOBOX controls the display of a horizontal box plot of the estimable function’s distribution across the posterior sample below the graph. The BOX option is enabled by default.
- HIST
 |
| NOHIST
NOHIST controls the display of the histogram of the estimable function’s distribution across the posterior sample. The HIST option is enabled by default.
- NORMAL
 |
| NONORMAL
NONORMAL controls the display of a normal density estimate on the graph. The NONORMAL option is enabled by default.
- KERNEL
 |
| NOKERNEL
NOKERNEL controls the display of a kernel density estimate on the graph. The KERNEL option is enabled by default.
- NROWS=number
specifies the highest number of rows in a panel. The default is 3.
- NCOLS=number
specifies the highest number of columns in a panel. The default is 3.
- UNPACK
unpacks the panel into separate graphics.
- BOX
- NONE
does not produce any plots.
- SEED=number
specifies the seed for the sampling-based components of the computations for the ESTIMATE statement (for example, chi-bar-square statistics and simulated p-values). number specifies an integer that is used to start the pseudo-random number generator for the simulation. If you do not specify a seed, or if you specify a value less than or equal to zero, the seed is generated from reading the time of day from the computer clock. There could be multiple ESTIMATE statements with SEED= specifications and there could be other statements that can supply a random number seed. Since the procedure has only one random number stream, the initial seed is shown in the SAS log.
- SINGULAR=number
tunes the estimability checking. If
 is a vector, define ABS(
is a vector, define ABS( ) to be the largest absolute value of the elements of
) to be the largest absolute value of the elements of  . If ABS(
. If ABS( ) is greater than
) is greater than  *number for any row of
*number for any row of 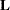 in the contrast, then
in the contrast, then 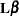 is declared nonestimable. Here,
is declared nonestimable. Here,  is the Hermite form matrix
is the Hermite form matrix 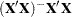 , and
, and  is ABS(
is ABS(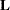 ), except when it equals 0, and then
), except when it equals 0, and then  is 1. The value for number must be between 0 and 1; the default is 1E
is 1. The value for number must be between 0 and 1; the default is 1E 4.
4. - STEPDOWN<(step-down-options)>
requests that multiplicity adjustments for the p-values of estimates be further adjusted in a step-down fashion. Step-down methods increase the power of multiple testing procedures by taking advantage of the fact that a p-value is never declared significant unless all smaller p-values are also declared significant. The STEPDOWN adjustment combined with ADJUST=BON corresponds to the methods of Holm (1979) and "Method 2" of Shaffer (1986); this is the default. Using step-down-adjusted p-values combined with ADJUST=SIMULATE corresponds to the method of Westfall (1997).
If the ESTIMATE statement is applied with a STEPDOWN option in a mixed model where the degrees-of-freedom method is that of Kenward and Roger (1997) or of Satterthwaite, then step-down-adjusted p-values are produced only if the ADJDFE=ROW option is in effect.
Also, the STEPDOWN option affects only p-values, not confidence limits. For ADJUST=SIMULATE, the generalized least squares hybrid approach of Westfall (1997) is used to increase Monte Carlo accuracy. You can specify the following step-down-options in parentheses after the STEPDOWN option:
- MAXTIME=n
specifies the time (in seconds) to be spent computing the maximal logically consistent sequential subsets of equality hypotheses for TYPE=LOGICAL. The default is MAXTIME=60. If the MAXTIME value is exceeded, the adjusted tests are not computed. When this occurs, you can try increasing the MAXTIME value. However, note that there are common multiple comparisons problems for which this computation requires a huge amount of time—for example, all pairwise comparisons between more than 10 groups. In such cases, try to use TYPE=FREE (the default) or TYPE=LOGICAL(
 ) for small
) for small  .
. - ORDER=PVALUE
- ORDER=ROWS
specifies the order in which the step-down tests to be performed. ORDER=PVALUE is the default, with estimates being declared significant only if all estimates with smaller (unadjusted) p-values are significant. If you specify ORDER=ROWS, then significances are evaluated in the order in which they are specified in the syntax.
- REPORT
specifies that a report on the step-down adjustment be displayed, including a listing of the sequential subsets (Westfall 1997) and, for ADJUST=SIMULATE, the step-down simulation results.
- TYPE=LOGICAL<(n)>
- TYPE=FREE
specifies how step-down adjustment are made. If you specify TYPE=LOGICAL, the step-down adjustments are computed by using maximal logically consistent sequential subsets of equality hypotheses (Shaffer 1986, Westfall 1997). Alternatively, for TYPE=FREE, sequential subsets are computed ignoring logical constraints. The TYPE=FREE results are more conservative than those for TYPE=LOGICAL, but they can be much more efficient to produce for many estimates. For example, it is not feasible to take logical constraints between all pairwise comparisons of more than about 10 groups. For this reason, TYPE=FREE is the default.
However, you can reduce the computational complexity of taking logical constraints into account by limiting the depth of the search tree used to compute them, specifying the optional depth parameter as a number
 in parentheses after TYPE=LOGICAL. As with TYPE=FREE, results for TYPE=LOGICAL(
in parentheses after TYPE=LOGICAL. As with TYPE=FREE, results for TYPE=LOGICAL( ) are conservative relative to the true TYPE=LOGICAL results. But even for TYPE=LOGICAL(
) are conservative relative to the true TYPE=LOGICAL results. But even for TYPE=LOGICAL(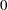 ) they can be appreciably less conservative than TYPE=FREE, and they are computationally feasible for much larger numbers of estimates. If you do not specify
) they can be appreciably less conservative than TYPE=FREE, and they are computationally feasible for much larger numbers of estimates. If you do not specify  or if
or if 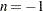 , the full search tree is used.
, the full search tree is used.
- TESTVALUE=value-list
- TESTMEAN=value-list
specifies the value under the null hypothesis for testing the estimable functions in the ESTIMATE statement. The rules for specifying the value-list are very similar to those for specifying the divisor list in the DIVISOR= option. If no TESTVALUE= is specified, all tests are performed as
 . Missing values in the value-list also are translated to zeros. If you specify fewer values than rows in the ESTIMATE statement, the last value in value-list is carried forward.
. Missing values in the value-list also are translated to zeros. If you specify fewer values than rows in the ESTIMATE statement, the last value in value-list is carried forward. The TESTVALUE= option affects only
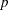 -values from individual, joint, and multiplicity-adjusted tests. It does not affect confidence intervals.
-values from individual, joint, and multiplicity-adjusted tests. It does not affect confidence intervals. The TESTVALUE option is not available for the multinomial distribution, and the values are ignored when you perform a sampling-based (Bayesian) analysis.
- UPPER
- UPPERTAILED
requests that the p-value for the t test be based only on values that are greater than the test statistic. A two-tailed test is the default. An upper-tailed confidence limit is also produced if you specify the CL or ALPHA= option.
Note that for ADJUST=SCHEFFE the one-sided adjusted confidence intervals and one-sided adjusted p-values are the same as the corresponding two-sided statistics, because this adjustment is based on only the right tail of the
 distribution.
distribution. If you request a joint test with the JOINT option, then a one-sided right-tailed order restriction is applied to all estimable functions, and the corresponding chi-bar-square statistic of Silvapulle and Sen (2004) is computed in addition to the two-sided, standard, F or chi-square statistic. See the JOINT option for how to control the computation of the simulation-based chi-bar-square statistic.
Copyright © SAS Institute, Inc. All Rights Reserved.
 )
) 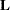 matrix
matrix