Silvapulle and Sen (2004) propose a test statistic for testing hypotheses where the null or the alternative hypothesis or both involve inequalities. You can test special cases of these hypotheses with the JOINT option in the ESTIMATE and the LSMESTIMATE statement. Consider the 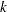estimable functions 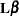and the hypotheses and 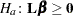. The alternative hypothesis defines a convex cone 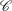at the origin. Suppose that under the null hypothesis 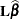follows a multivariate normal distribution with mean 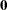and variance 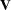. The restricted alternative prevents you from using the usual or chi-square test machinery, since the distribution of the test statistic under the alternative might not follow the usual rules. Silvapulle and Sen (2004) coined a statistic that takes into account the projection of the observed estimate onto the convex cone formed by the alternative parameter space. This test statistic is called the chi-bar-square statistic, and 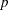-values are obtained by simulation; see, in particular, Chapter 3.4 in Silvapulle and Sen (2004).

Briefly, let 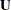be a multivariate normal random variable with mean 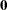and variance matrix 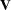. The chi-bar-square statistic is the random variable

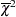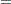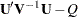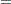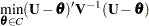and it can be motivated by a geometric argument. The quadratic form in is the 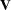-projection of 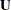onto the cone 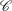. Suppose that this projected point is . If , then and . If 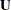is completely outside of the cone 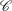, then is a point on the surface of the cone. Similarly, 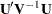is the length of the segment from the origin to 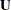in the 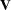-space with norm 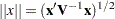. If you apply the Pythagorean theorem, you can see that the chi-bar-square statistic measures the length of the segment from the origin to the projected point in .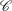

To calculate 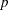-values for chi-bar-square statistics, a simulation-based approach is taken. Consider again the set of 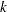estimable functions 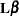with estimate and variance .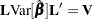

First, the observed value of the statistic is computed as

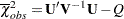Then, independent random samples 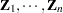are drawn from an distribution and the following chi-bar-statistics are computed for the sample:

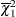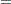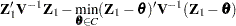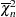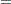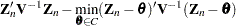The 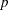-value is estimated by the fraction of simulated statistics that are greater than or equal to the observed value .

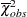Notice that unless 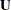is interior to the cone 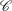, finding the value of requires the solution to a quadratic optimization problem. When 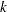is large, or when many simulations are requested, the computation of 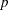-values for chi-bar-square statistics might require considerable computing time.