PROC GLM: LSMEANS Statement :: SAS/STAT(R) 9.22 User's Guide

The GLM Procedure

LSMEANS Statement

LSMEANS effects </ options> ;

Least squares means (LS-means) are computed for each effect listed in the LSMEANS statement. You can specify only classification effects in the LSMEANS statement—that is, effects that contain only classification variables. You can also specify options to perform multiple comparisons. In contrast to the MEANS statement, the LSMEANS statement performs multiple comparisons on interactions as well as main effects.

LS-means are predicted population margins; that is, they estimate the marginal means over a balanced population. In a sense, LS-means are to unbalanced designs as class and subclass arithmetic means are to balanced designs. Each LS-mean is computed as 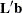$\text{[math]}$ for a certain column vector 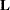$\text{[math]}$ , where $\text{[math]}$ is the vector of parameter estimates—that is, the solution of the normal equations. For further information, see the section Construction of Least Squares Means.

Multiple effects can be specified in one LSMEANS statement, or multiple LSMEANS statements can be used, but they must all appear after the MODEL statement. For example:

proc glm;
   class A B;
   model Y=A B A*B;
   lsmeans A B A*B;
run;

LS-means are displayed for each level of the A, B, and A*B effects.

You can specify the following options in the LSMEANS statement after a slash (/):

ADJUST=BON

ADJUST=DUNNETT

ADJUST=NELSON

ADJUST=SCHEFFE

ADJUST=SIDAK

ADJUST=SIMULATE <(simoptions)>

ADJUST=SMM | GT2

ADJUST=TUKEY

ADJUST=T

requests a multiple comparison adjustment for the p-values and confidence limits for the differences of LS-means. The ADJUST= option modifies the results of the TDIFF and PDIFF options; thus, if you omit the TDIFF or PDIFF option then the ADJUST= option has no effect. By default, PROC GLM analyzes all pairwise differences. If you specify ADJUST=DUNNETT, PROC GLM analyzes all differences with a control level. If you specify the ADJUST=NELSON option, PROC GLM analyzes all differences with the average LS-mean. The default is ADJUST=T, which really signifies no adjustment for multiple comparisons.

The BON (Bonferroni) and SIDAK adjustments involve correction factors described in the section Multiple Comparisons and in Chapter 58, The MULTTEST Procedure. When you specify ADJUST=TUKEY and your data are unbalanced, PROC GLM uses the approximation described in Kramer (1956) and identifies the adjustment as "Tukey-Kramer" in the results. Similarly, when you specify either ADJUST=DUNNETT or the ADJUST=NELSON option and the LS-means are correlated, PROC GLM uses the factor-analytic covariance approximation described in Hsu (1992) and identifies the adjustment in the results as "Dunnett-Hsu" or "Nelson-Hsu," respectively. The preceding references also describe the SCHEFFE and SMM adjustments.

The SIMULATE adjustment computes the adjusted p-values from the simulated distribution of the maximum or maximum absolute value of a multivariate t random vector. The simulation estimates 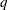$\text{[math]}$ , the true 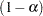$\text{[math]}$ th quantile, where $\text{[math]}$ is the confidence coefficient. The default $\text{[math]}$ is the value of the ALPHA= option in the PROC GLM statement or 0.05 if that option is not specified. You can change this value with the ALPHA= option in the LSMEANS statement.

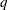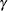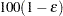The number of samples for the SIMULATE adjustment is set so that the tail area for the simulated $\text{[math]}$ is within a certain accuracy radius $\text{[math]}$ of $\text{[math]}$ with an accuracy confidence of $\text{[math]}$ %. In equation form,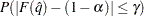

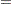
$\text{[math]}$

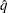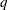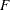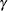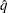where $\text{[math]}$ is the simulated $\text{[math]}$ and $\text{[math]}$ is the true distribution function of the maximum; see Edwards and Berry (1987) for details. By default, $\text{[math]}$ = 0.005 and $\text{[math]}$ = 0.01, so that the tail area of $\text{[math]}$ is within 0.005 of 0.95 with 99% confidence.

You can specify the following simoptions in parentheses after the ADJUST=SIMULATE option.

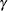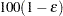ACC=value: specifies the target accuracy radius $\text{[math]}$ of a $\text{[math]}$ % confidence interval for the true probability content of the estimated 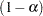$\text{[math]}$ th quantile. The default value is ACC=0.005. Note that, if you also specify the CVADJUST simoption, then the actual accuracy radius will probably be substantially less than this target.
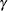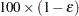CVADJUST: specifies that the quantile should be estimated by the control variate adjustment method of Hsu and Nelson (1998) instead of simply as the quantile of the simulated sample. Specifying the CVADJUST option typically has the effect of significantly reducing the accuracy radius $\text{[math]}$ of a $\text{[math]}$ % confidence interval for the true probability content of the estimated 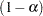$\text{[math]}$ th quantile. The control-variate-adjusted quantile estimate takes roughly twice as long to compute, but it is typically much more accurate than the sample quantile.
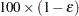EPS=value: specifies the value $\text{[math]}$ for a $\text{[math]}$ % confidence interval for the true probability content of the estimated 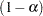$\text{[math]}$ th quantile. The default value for the accuracy confidence is 99%, corresponding to EPS=0.01.
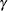NSAMP=n: specifies the sample size for the simulation. By default, $\text{[math]}$ is set based on the values of the target accuracy radius $\text{[math]}$ and accuracy confidence 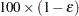$\text{[math]}$ % for an interval for the true probability content of the estimated 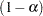$\text{[math]}$ th quantile. With the default values for 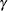$\text{[math]}$ , $\text{[math]}$ , and $\text{[math]}$ (0.005, 0.01, and 0.05, respectively), NSAMP=12604 by default.
REPORT: specifies that a report on the simulation should be displayed, including a listing of the parameters, such as 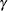$\text{[math]}$ , $\text{[math]}$ , and $\text{[math]}$ , as well as an analysis of various methods for estimating or approximating the quantile.
SEED=number: specifies an integer used to start the pseudo-random number generator for the simulation. If you do not specify a seed, or specify a value less than or equal to zero, the seed is by default generated from reading the time of day from the computer’s clock.
THREADS: specifies that the computational work for the simulation be divided into parallel threads, where the number of threads is the value of the SAS system option CPUCOUNT=. For large simulations (as specified directly using the NSAMP= simoption or indirectly using the ACC= or EPS= simoptions), parallel processing can markedly speed up the computation of adjusted p-values and confidence intervals. However, because the parallel processing has different pseudo-random number streams, the precise results are different from the default ones, which are computed in sequence rather than in parallel. This option overrides the SAS system option THREADS | NOTHREADS.
NOTHREADS: specifies that the computational work for the simulation be performed in sequence rather than in parallel. NOTHREADS is the default. This option overrides the SAS system option THREADS | NOTHREADS.

ALPHA=p

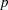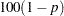specifies the level of significance $\text{[math]}$ for $\text{[math]}$ % confidence intervals. This option is useful only if you also specify the CL option, and, optionally, the PDIFF option. By default, 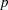$\text{[math]}$ is equal to the value of the ALPHA= option in the PROC GLM statement or 0.05 if that option is not specified, This value is used to set the endpoints for confidence intervals for the individual means as well as for differences between means.

AT variable = value

AT (variable-list) = (value-list)

AT MEANS

enables you to modify the values of the covariates used in computing LS-means. By default, all covariate effects are set equal to their mean values for computation of standard LS-means. The AT option enables you to set the covariates to whatever values you consider interesting. For more information, see the section Setting Covariate Values.

BYLEVEL

requests that PROC GLM process the OM data set by each level of the LS-mean effect in question. For more details, see the entry for the OM option in this section.

CL

requests confidence limits for the individual LS-means. If you specify the PDIFF option, confidence limits for differences between means are produced as well. You can control the confidence level with the ALPHA= option. Note that, if you specify an ADJUST= option, the confidence limits for the differences are adjusted for multiple inference but the confidence intervals for individual means are not adjusted.

COV

includes variances and covariances of the LS-means in the output data set specified in the OUT= option in the LSMEANS statement. Note that this is the covariance matrix for the LS-means themselves, not the covariance matrix for the differences between the LS-means, which is used in the PDIFF computations. If you omit the OUT= option, the COV option has no effect. When you specify the COV option, you can specify only one effect in the LSMEANS statement.

E

displays the coefficients of the linear functions used to compute the LS-means.

E=effect

specifies an effect in the model to use as an error term. The procedure uses the mean square for the effect as the error mean square when calculating estimated standard errors (requested with the STDERR option) and probabilities (requested with the STDERR, PDIFF, or TDIFF option). Unless you specify STDERR, PDIFF or TDIFF, the E= option is ignored. By default, if you specify the STDERR, PDIFF, or TDIFF option and do not specify the E= option, the procedure uses the error mean square for calculating standard errors and probabilities.

ETYPE=n

specifies the type (1, 2, 3, or 4, corresponding to a Type I, II, III, or IV test, respectively) of the E= effect. If you specify the E= option but not the ETYPE= option, the highest type computed in the analysis is used. If you omit the E= option, the ETYPE= option has no effect.

LINES

presents results of comparisons between all pairs of means (specified by the PDIFF=ALL option) by listing the means in descending order and indicating nonsignificant subsets by line segments beside the corresponding means. When all differences have the same variance, these comparison lines are guaranteed to accurately reflect the inferences based on the corresponding tests, made by comparing the respective 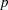$\text{[math]}$ -values to the value of the ALPHA= option (0.05 by default). However, equal variances are rarely the case for differences between LS-means. If the variances are not all the same, then the comparison lines might be conservative, in the sense that if you base your inferences on the lines alone, you will detect fewer significant differences than the tests indicate. If there are any such differences, a note is appended to the table that lists the pairs of means that are inferred to be significantly different by the tests but not by the comparison lines. Note, however, that in many cases, even though the variances are unbalanced, they are near enough that the comparison lines in fact accurately reflect the test inferences.

NOPRINT

suppresses the normal display of results from the LSMEANS statement. This option is useful when an output data set is created with the OUT= option in the LSMEANS statement.

OBSMARGINS

OM

specifies a potentially different weighting scheme for computing LS-means coefficients. The standard LS-means have equal coefficients across classification effects; however, the OM option changes these coefficients to be proportional to those found in the input data set. For more information, see the section Changing the Weighting Scheme.

The BYLEVEL option modifies the observed-margins LS-means. Instead of computing the margins across the entire data set, the procedure computes separate margins for each level of the LS-mean effect in question. The resulting LS-means are actually equal to raw means in this case. If you specify the BYLEVEL option, it disables the AT option.

OUT=SAS-data-set

creates an output data set that contains the values, standard errors, and, optionally, the covariances (see the COV option) of the LS-means.

For more information, see the section Output Data Sets.

PDIFF<=difftype>

requests that 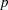$\text{[math]}$ -values for differences of the LS-means be produced. The optional difftype specifies which differences to display. Possible values for difftype are ALL, CONTROL, CONTROLL, CONTROLU, and ANOM. The ALL value requests all pairwise differences, and it is the default. The CONTROL value requests the differences with a control that, by default, is the first level of each of the specified LS-mean effects. The ANOM value requests differences between each LS-mean and the average LS-mean, as in the analysis of means (Ott; 1967). The average is computed as a weighted mean of the LS-means, the weights being inversely proportional to the variances. Note that the ANOM procedure in SAS/QC software implements both tables and graphics for the analysis of means with a variety of response types. For one-way designs, the PDIFF=ANOM computations are equivalent to the results of PROC ANOM. See the section Analysis of Means: Comparing Each Treatments to the Average for more details.

To specify which levels of the effects are the controls, list the quoted formatted values in parentheses after the keyword CONTROL. For example, if the effects A, B, and C are CLASS variables, each having two levels, ’1’ and ’2’, the following LSMEANS statement specifies the ’1’ ’2’ level of A*B and the ’2’ ’1’ level of B*C as controls:

lsmeans A*B B*C / pdiff=control('1' '2', '2' '1');

For multiple-effect situations such as this one, the ordering of the list is significant, and you should check the output to make sure that the controls are correct.

Two-tailed tests and confidence limits are associated with the CONTROL difftype. For one-tailed results, use either the CONTROLL or CONTROLU difftype.

PDIFF=CONTROLL tests whether the noncontrol levels are less than the control; you declare a noncontrol level to be significantly less than the control if the associated upper confidence limit for the noncontrol level minus the control is less than zero, and you ignore the associated lower confidence limits (which are set to minus infinity).
PDIFF=CONTROLU tests whether the noncontrol levels are greater than the control; you declare a noncontrol level to be significantly greater than the control if the associated lower confidence limit for the noncontrol level minus the control is greater than zero, and you ignore the associated upper confidence limits (which are set to infinity).

The default multiple comparisons adjustment for each difftype is shown in the following table.

*difftype*	Default ADJUST=
Not specified	T
ALL	TUKEY
CONTROL
CONTROLL	DUNNETT
CONTROLU
ANOM	NELSON

If no difftype is specified, the default for the ADJUST= option is T (that is, no adjustment); for PDIFF=ALL, ADJUST=TUKEY is the default; for PDIFF=CONTROL, PDIFF=CONTROLL, or PDIFF=CONTROLU, the default value for the ADJUST= option is DUNNETT. For PDIFF=ANOM, ADJUST=NELSON is the default. If there is a conflict between the PDIFF= and ADJUST= options, the ADJUST= option takes precedence.

For example, in order to compute one-sided confidence limits for differences with a control, adjusted according to Dunnett’s procedure, the following statements are equivalent:

lsmeans Treatment / pdiff=controll cl;
lsmeans Treatment / pdiff=controll cl adjust=dunnett;

SLICE=fixed-effect

SLICE=(fixed-effects)

specifies effects within which to test for differences between interaction LS-mean effects. This can produce what are known as tests of simple effects (Winer; 1971). For example, suppose that A*B is significant and you want to test for the effect of A within each level of B. The appropriate LSMEANS statement is

lsmeans A*B / slice=B;

This statement tests for the simple main effects of A for B, which are calculated by extracting the appropriate rows from the coefficient matrix for the A*B LS-means and using them to form an F test as performed by the CONTRAST statement.

SINGULAR=number

tunes the estimability checking. If ABS 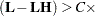$\text{[math]}$ number for any row, then 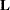$\text{[math]}$ is declared nonestimable. 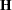$\text{[math]}$ is the 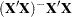$\text{[math]}$ matrix, and 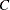$\text{[math]}$ is ABS 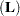$\text{[math]}$ except for rows where 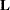$\text{[math]}$ is zero, and then it is 1. The default value for the SINGULAR= option is $\text{[math]}$ . Values for the SINGULAR= option must be between 0 and 1.

STDERR

produces the standard error of the LS-means and the probability level for the hypothesis $\text{[math]}$ .

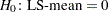TDIFF

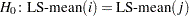produces the $\text{[math]}$ values for all hypotheses $\text{[math]}$ and the corresponding probabilities.

Top of Page