| The GLM Procedure |
| PROC GLM for Unbalanced ANOVA |
Analysis of variance, or ANOVA, typically refers to partitioning the variation in a variable’s values into variation between and within several groups or classes of observations. The GLM procedure can perform simple or complicated ANOVA for balanced or unbalanced data.
This example discusses the analysis of variance for the unbalanced 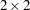 data shown in Table 39.1. The experimental design is a full factorial, in which each level of one treatment factor occurs at each level of the other treatment factor. Note that there is only one value for the cell with A=‘A2’ and B=‘B2’. Since one cell contains a different number of values from the other cells in the table, this is an unbalanced design.
data shown in Table 39.1. The experimental design is a full factorial, in which each level of one treatment factor occurs at each level of the other treatment factor. Note that there is only one value for the cell with A=‘A2’ and B=‘B2’. Since one cell contains a different number of values from the other cells in the table, this is an unbalanced design.
|
A1 |
A2 |
B1 |
12, 14 |
20, 18 |
B2 |
11, 9 |
17 |
The following statements read the data into a SAS data set and then invoke PROC GLM to produce the analysis.
title 'Analysis of Unbalanced 2-by-2 Factorial'; data exp; input A $ B $ Y @@; datalines; A1 B1 12 A1 B1 14 A1 B2 11 A1 B2 9 A2 B1 20 A2 B1 18 A2 B2 17 ;
proc glm data=exp; class A B; model Y=A B A*B; run;
Both treatments are listed in the CLASS statement because they are classification variables. A*B denotes the interaction of the A effect and the B effect. The results are shown in Figure 39.1 and Figure 39.2.
Figure 39.1 displays information about the classes as well as the number of observations in the data set. Figure 39.2 shows the ANOVA table, simple statistics, and tests of effects.
| Analysis of Unbalanced 2-by-2 Factorial |
| Source | DF | Sum of Squares | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Model | 3 | 91.71428571 | 30.57142857 | 15.29 | 0.0253 |
| Error | 3 | 6.00000000 | 2.00000000 | ||
| Corrected Total | 6 | 97.71428571 |
The degrees of freedom can be used to check your data. The Model degrees of freedom for a 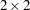 factorial design with interaction are
factorial design with interaction are 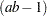 , where
, where  is the number of levels of A and
is the number of levels of A and 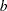 is the number of levels of B; in this case,
is the number of levels of B; in this case, 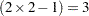 . The Corrected Total degrees of freedom are always one less than the number of observations used in the analysis; in this case,
. The Corrected Total degrees of freedom are always one less than the number of observations used in the analysis; in this case, 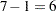 .
.
The overall 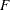 test is significant
test is significant  , indicating strong evidence that the means for the four different A
, indicating strong evidence that the means for the four different A B cells are different. You can further analyze this difference by examining the individual tests for each effect.
B cells are different. You can further analyze this difference by examining the individual tests for each effect.
Four types of estimable functions of parameters are available for testing hypotheses in PROC GLM. For data with no missing cells, the Type III and Type IV estimable functions are the same and test the same hypotheses that would be tested if the data were balanced. Type I and Type III sums of squares are typically not equal when the data are unbalanced; Type III sums of squares are preferred in testing effects in unbalanced cases because they test a function of the underlying parameters that is independent of the number of observations per treatment combination.
According to a significance level of 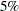
 , the A*B interaction is not significant
, the A*B interaction is not significant 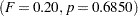 . This indicates that the effect of A does not depend on the level of B and vice versa. Therefore, the tests for the individual effects are valid, showing a significant A effect
. This indicates that the effect of A does not depend on the level of B and vice versa. Therefore, the tests for the individual effects are valid, showing a significant A effect 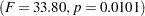 but no significant B effect
but no significant B effect 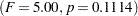 .
.
If you enable ODS Graphics, GLM also displays by default an interaction plot for this analysis. The following statements, which are the same as in the previous analysis but with ODS Graphics enabled, additionally produce Figure 39.3.
ods graphics on; proc glm data=exp; class A B; model Y=A B A*B; run; ods graphics off;
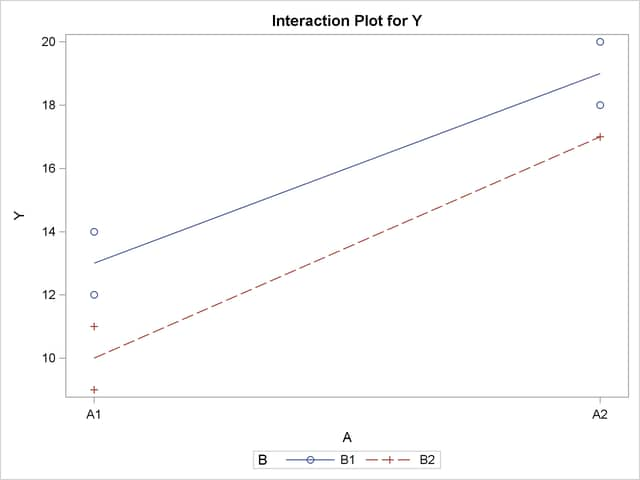
The insignificance of the A*B interaction is reflected in the fact that two lines in Figure 39.3 are nearly parallel. For more information about the graphics that GLM can produce, see the section ODS Graphics.
Copyright © SAS Institute, Inc. All Rights Reserved.