| The LOGISTIC Procedure |
| OUTPUT Statement |
The OUTPUT statement creates a new SAS data set that contains all the variables in the input data set and, optionally, the estimated linear predictors and their standard error estimates, the estimates of the cumulative or individual response probabilities, and the confidence limits for the cumulative probabilities. Regression diagnostic statistics and estimates of cross validated response probabilities are also available for binary response models. If you specify more than one OUTPUT statement, only the last one is used. Formulas for the statistics are given in the sections Linear Predictor, Predicted Probability, and Confidence Limits and Regression Diagnostics, and, for conditional logistic regression, in the section Conditional Logistic Regression.
If you use the single-trial syntax, the data set also contains a variable named _LEVEL_, which indicates the level of the response that the given row of output is referring to. For instance, the value of the cumulative probability variable is the probability that the response variable is as large as the corresponding value of _LEVEL_. For details, see the section OUT= Output Data Set in the OUTPUT Statement.
The estimated linear predictor, its standard error estimate, all predicted probabilities, and the confidence limits for the cumulative probabilities are computed for all observations in which the explanatory variables have no missing values, even if the response is missing. By adding observations with missing response values to the input data set, you can compute these statistics for new observations or for settings of the explanatory variables not present in the data without affecting the model fit. Alternatively, the SCORE statement can be used to compute predicted probabilities and confidence intervals for new observations.
Table 51.3 lists the available options, which can be specified after a slash (/). The statistic and diagnostic options specify the statistics to be included in the output data set and name the new variables that contain the statistics. If a STRATA statement is specified, only the PREDICTED=, DFBETAS=, and H= options are available; see the section Regression Diagnostic Details for details.
Option |
Description |
|---|---|
specifies |
|
names the output data set |
|
Statistic Options |
|
names the lower confidence limit |
|
names the predicted probabilities |
|
requests the individual, cumulative, or cross validated predicted probabilities |
|
names the standard error estimate of the linear predictor |
|
names the upper confidence limit |
|
names the linear predictor |
|
Diagnostic Options for Binary Response |
|
names the confidence interval displacement |
|
names the confidence interval displacement |
|
names the standardized deletion parameter differences |
|
names the deletion chi-square goodness-of-fit change |
|
names the deletion deviance change |
|
names the leverage |
|
names the Pearson chi-square residual |
|
names the deviance residual |
|
The following list describes these options.
- ALPHA=number
sets the level of significance
 for
for  % confidence limits for the appropriate response probabilities. The value of number must be between 0 and 1. By default, number is equal to the value of the ALPHA= option in the PROC LOGISTIC statement, or 0.05 if that option is not specified.
% confidence limits for the appropriate response probabilities. The value of number must be between 0 and 1. By default, number is equal to the value of the ALPHA= option in the PROC LOGISTIC statement, or 0.05 if that option is not specified. - C=name
specifies the confidence interval displacement diagnostic that measures the influence of individual observations on the regression estimates.
- CBAR=name
specifies the confidence interval displacement diagnostic that measures the overall change in the global regression estimates due to deleting an individual observation.
- DFBETAS=_ALL_
- DFBETAS=var-list
specifies the standardized differences in the regression estimates for assessing the effects of individual observations on the estimated regression parameters in the fitted model. You can specify a list of up to
 variable names, where
variable names, where  is the number of explanatory variables in the MODEL statement, or you can specify just the keyword _ALL_. In the former specification, the first variable contains the standardized differences in the intercept estimate, the second variable contains the standardized differences in the parameter estimate for the first explanatory variable in the MODEL statement, and so on. In the latter specification, the DFBETAS statistics are named DFBETA_
is the number of explanatory variables in the MODEL statement, or you can specify just the keyword _ALL_. In the former specification, the first variable contains the standardized differences in the intercept estimate, the second variable contains the standardized differences in the parameter estimate for the first explanatory variable in the MODEL statement, and so on. In the latter specification, the DFBETAS statistics are named DFBETA_ , where
, where  is the name of the regression parameter. For example, if the model contains two variables X1 and X2, the specification DFBETAS=_ALL_ produces three DFBETAS statistics: DFBETA_Intercept, DFBETA_X1, and DFBETA_X2. If an explanatory variable is not included in the final model, the corresponding output variable named in DFBETAS=var-list contains missing values.
is the name of the regression parameter. For example, if the model contains two variables X1 and X2, the specification DFBETAS=_ALL_ produces three DFBETAS statistics: DFBETA_Intercept, DFBETA_X1, and DFBETA_X2. If an explanatory variable is not included in the final model, the corresponding output variable named in DFBETAS=var-list contains missing values. - DIFCHISQ=name
specifies the change in the chi-square goodness-of-fit statistic attributable to deleting the individual observation.
- DIFDEV=name
specifies the change in the deviance attributable to deleting the individual observation.
- H=name
specifies the diagonal element of the hat matrix for detecting extreme points in the design space.
- LOWER=name
- L=name
names the variable containing the lower confidence limits for
 , where
, where  is the probability of the event response if events/trials syntax or single-trial syntax with binary response is specified; for a cumulative model,
is the probability of the event response if events/trials syntax or single-trial syntax with binary response is specified; for a cumulative model,  is cumulative probability (that is, the probability that the response is less than or equal to the value of _LEVEL_); for the generalized logit model, it is the individual probability (that is, the probability that the response category is represented by the value of _LEVEL_). See the ALPHA= option to set the confidence level.
is cumulative probability (that is, the probability that the response is less than or equal to the value of _LEVEL_); for the generalized logit model, it is the individual probability (that is, the probability that the response category is represented by the value of _LEVEL_). See the ALPHA= option to set the confidence level. - OUT=SAS-data-set
names the output data set. If you omit the OUT= option, the output data set is created and given a default name by using the DATA
 convention.
convention. - PREDICTED=name
- PRED=name
- PROB=name
- P=name
names the variable containing the predicted probabilities. For the events/trials syntax or single-trial syntax with binary response, it is the predicted event probability. For a cumulative model, it is the predicted cumulative probability (that is, the probability that the response variable is less than or equal to the value of _LEVEL_); and for the generalized logit model, it is the predicted individual probability (that is, the probability of the response category represented by the value of _LEVEL_).
- PREDPROBS=(keywords)
requests individual, cumulative, or cross validated predicted probabilities. Descriptions of the keywords are as follows.
- INDIVIDUAL | I
requests the predicted probability of each response level. For a response variable Y with three levels, 1, 2, and 3, the individual probabilities are Pr(Y
 1), Pr(Y
1), Pr(Y 2), and Pr(Y
2), and Pr(Y 3).
3). - CUMULATIVE | C
requests the cumulative predicted probability of each response level. For a response variable Y with three levels, 1, 2, and 3, the cumulative probabilities are Pr(Y
 1), Pr(Y
1), Pr(Y 2), and Pr(Y
2), and Pr(Y 3). The cumulative probability for the last response level always has the constant value of 1. For generalized logit models, the cumulative predicted probabilities are not computed and are set to missing.
3). The cumulative probability for the last response level always has the constant value of 1. For generalized logit models, the cumulative predicted probabilities are not computed and are set to missing. - CROSSVALIDATE | XVALIDATE | X
requests the cross validated individual predicted probability of each response level. These probabilities are derived from the leave-one-out principle—that is, dropping the data of one subject and reestimating the parameter estimates. PROC LOGISTIC uses a less expensive one-step approximation to compute the parameter estimates. This option is valid only for binary response models; for nominal and ordinal models, the cross validated probabilities are not computed and are set to missing.
See the section Details of the PREDPROBS= Option at the end of this section for further details.
- RESCHI=name
specifies the Pearson (chi-square) residual for identifying observations that are poorly accounted for by the model.
- RESDEV=name
specifies the deviance residual for identifying poorly fitted observations.
- STDXBETA=name
names the variable containing the standard error estimates of XBETA. See the section Linear Predictor, Predicted Probability, and Confidence Limits for details.
- UPPER=name
- U=name
names the variable containing the upper confidence limits for
 , where
, where  is the probability of the event response if events/trials syntax or single-trial syntax with binary response is specified; for a cumulative model,
is the probability of the event response if events/trials syntax or single-trial syntax with binary response is specified; for a cumulative model,  is cumulative probability (that is, the probability that the response is less than or equal to the value of _LEVEL_); for the generalized logit model, it is the individual probability (that is, the probability that the response category is represented by the value of _LEVEL_). See the ALPHA= option to set the confidence level.
is cumulative probability (that is, the probability that the response is less than or equal to the value of _LEVEL_); for the generalized logit model, it is the individual probability (that is, the probability that the response category is represented by the value of _LEVEL_). See the ALPHA= option to set the confidence level. - XBETA=name
names the variable containing the estimates of the linear predictor
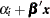 , where
, where  is the corresponding ordered value of _LEVEL_.
is the corresponding ordered value of _LEVEL_.
Details of the PREDPROBS= Option
You can request any of the three types of predicted probabilities. For example, you can request both the individual predicted probabilities and the cross validated probabilities by specifying PREDPROBS=(I X).
When you specify the PREDPROBS= option, two automatic variables, _FROM_ and _INTO_, are included for the single-trial syntax and only one variable, _INTO_, is included for the events/trials syntax. The variable _FROM_ contains the formatted value of the observed response. The variable _INTO_ contains the formatted value of the response level with the largest individual predicted probability.
If you specify PREDPROBS=INDIVIDUAL, the OUT= data set contains 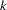 additional variables representing the individual probabilities, one for each response level, where
additional variables representing the individual probabilities, one for each response level, where 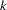 is the maximum number of response levels across all BY groups. The names of these variables have the form IP_xxx, where xxx represents the particular level. The representation depends on the following situations:
is the maximum number of response levels across all BY groups. The names of these variables have the form IP_xxx, where xxx represents the particular level. The representation depends on the following situations:
If you specify events/trials syntax, xxx is either ‘Event’ or ‘Nonevent’. Thus, the variable containing the event probabilities is named IP_Event and the variable containing the nonevent probabilities is named IP_Nonevent.
If you specify the single-trial syntax with more than one BY group, xxx is 1 for the first ordered level of the response, 2 for the second ordered level of the response, and so forth, as given in the "Response Profile" table. The variable containing the predicted probabilities Pr(Y=1) is named IP_1, where Y is the response variable. Similarly, IP_2 is the name of the variable containing the predicted probabilities Pr(Y=2), and so on.
If you specify the single-trial syntax with no BY-group processing, xxx is the left-justified formatted value of the response level (the value might be truncated so that IP_xxx does not exceed 32 characters). For example, if Y is the response variable with response levels ‘None’, ‘Mild’, and ‘Severe’, the variables representing individual probabilities Pr(Y=’None’), P(Y=’Mild’), and P(Y=’Severe’) are named IP_None, IP_Mild, and IP_Severe, respectively.
If you specify PREDPROBS=CUMULATIVE, the OUT= data set contains 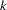 additional variables representing the cumulative probabilities, one for each response level, where
additional variables representing the cumulative probabilities, one for each response level, where 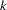 is the maximum number of response levels across all BY groups. The names of these variables have the form CP_xxx, where xxx represents the particular response level. The naming convention is similar to that given by PREDPROBS=INDIVIDUAL. The PREDPROBS=CUMULATIVE values are the same as those output by the PREDICT= option, but are arranged in variables on each output observation rather than in multiple output observations.
is the maximum number of response levels across all BY groups. The names of these variables have the form CP_xxx, where xxx represents the particular response level. The naming convention is similar to that given by PREDPROBS=INDIVIDUAL. The PREDPROBS=CUMULATIVE values are the same as those output by the PREDICT= option, but are arranged in variables on each output observation rather than in multiple output observations.
If you specify PREDPROBS=CROSSVALIDATE, the OUT= data set contains 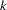 additional variables representing the cross validated predicted probabilities of the
additional variables representing the cross validated predicted probabilities of the 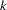 response levels, where
response levels, where 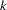 is the maximum number of response levels across all BY groups. The names of these variables have the form XP_xxx, where xxx represents the particular level. The representation is the same as that given by PREDPROBS=INDIVIDUAL except that for the events/trials syntax there are four variables for the cross validated predicted probabilities instead of two:
is the maximum number of response levels across all BY groups. The names of these variables have the form XP_xxx, where xxx represents the particular level. The representation is the same as that given by PREDPROBS=INDIVIDUAL except that for the events/trials syntax there are four variables for the cross validated predicted probabilities instead of two:
- XP_EVENT_R1E
is the cross validated predicted probability of an event when a current event trial is removed.
- XP_NONEVENT_R1E
is the cross validated predicted probability of a nonevent when a current event trial is removed.
- XP_EVENT_R1N
is the cross validated predicted probability of an event when a current nonevent trial is removed.
- XP_NONEVENT_R1N
is the cross validated predicted probability of a nonevent when a current nonevent trial is removed.
The cross validated predicted probabilities are precisely those used in the CTABLE option. See the section Predicted Probability of an Event for Classification for details of the computation.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
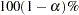 confidence intervals
confidence intervals