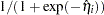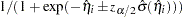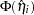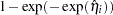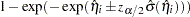| The LOGISTIC Procedure |
| Linear Predictor, Predicted Probability, and Confidence Limits |
This section describes how predicted probabilities and confidence limits are calculated by using the maximum likelihood estimates (MLEs) obtained from PROC LOGISTIC. For a specific example, see the section Getting Started: LOGISTIC Procedure. Predicted probabilities and confidence limits can be output to a data set with the OUTPUT statement.
Binary and Cumulative Response Models
For a vector of explanatory variables  , the linear predictor
, the linear predictor
 |
is estimated by
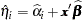 |
where 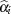 and
and 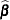 are the MLEs of
are the MLEs of 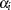 and
and  . The estimated standard error of
. The estimated standard error of 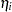 is
is 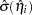 , which can be computed as the square root of the quadratic form
, which can be computed as the square root of the quadratic form 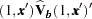 , where
, where 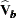 is the estimated covariance matrix of the parameter estimates. The asymptotic
is the estimated covariance matrix of the parameter estimates. The asymptotic 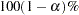 confidence interval for
confidence interval for 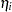 is given by
is given by
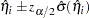 |
where 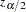 is the
is the 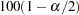 percentile point of a standard normal distribution.
percentile point of a standard normal distribution.
The predicted probability and the 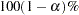 confidence limits for
confidence limits for  are obtained by back-transforming the corresponding measures for the linear predictor, as shown in the following table:
are obtained by back-transforming the corresponding measures for the linear predictor, as shown in the following table:
Link |
Predicted Probability |
100(1– |
|---|---|---|
LOGIT |
|
|
PROBIT |
|
|
CLOGLOG |
|
|
The CONTRAST statement also enables you to estimate the exponentiated contrast, 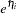 . The corresponding standard error is
. The corresponding standard error is 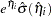 , and the confidence limits are computed by exponentiating those for the linear predictor:
, and the confidence limits are computed by exponentiating those for the linear predictor:  .
.
Generalized Logit Model
For a vector of explanatory variables  , define the linear predictors
, define the linear predictors 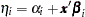 , and let
, and let 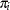 denote the probability of obtaining the response value
denote the probability of obtaining the response value  :
:
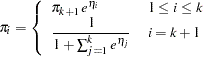 |
By the delta method,
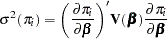 |
A 100(1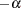 )% confidence level for
)% confidence level for 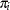 is given by
is given by
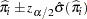 |
where 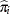 is the estimated expected probability of response
is the estimated expected probability of response  , and
, and 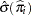 is obtained by evaluating
is obtained by evaluating 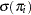 at
at 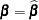 .
.
Note that the contrast 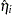 and exponentiated contrast
and exponentiated contrast 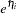 , their standard errors, and their confidence intervals are computed in the same fashion as for the cumulative response models, replacing
, their standard errors, and their confidence intervals are computed in the same fashion as for the cumulative response models, replacing  with
with 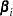 .
.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
 )% Confidence Limits
)% Confidence Limits