The Network Solver

Connected Components

Subsections:

Connected Components of a Simple Undirected Graph
Connected Components of a Simple Directed Graph

A connected component of a graph is a set of nodes that are all reachable from each other. That is, if two nodes are in the same component, then there exists a path between them. For a directed graph, there are two types of components: a strongly connected component has a directed path between any two nodes, and a weakly connected component ignores direction and requires only that a path exist between any two nodes.

In the network solver, you can invoke connected components by using the CONCOMP= option.

There are two main algorithms for finding connected components in an undirected graph: a depth-first search algorithm (ALGORITHM= DFS) and a union-find algorithm (ALGORITHM=UNION_FIND). For a graph 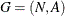$G = (N,A)$ , both algorithms run in time 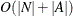$O(|N|+|A|)$ and can usually scale to very large graphs. The default is the union-find algorithm. For directed graphs, only the depth-first search algorithm is available.

The results of the connected components algorithm are written to the node-indexed numeric array that you specify in the CONCOMP= suboption of the OUT= option. For each node in the set, the value of this array identifies its component. The component identifiers are numbered sequentially starting from 1.

Connected Components of a Simple Undirected Graph

This section illustrates the use of the connected components algorithm on the simple undirected graph G that is shown in Figure 9.23.

Figure 9.23: A Simple Undirected Graph G

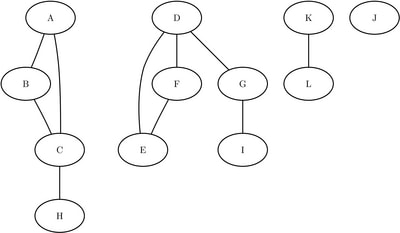
The undirected graph G can be represented by the following links data set, LinkSetIn:

data LinkSetIn;
   input from $ to $ @@;
   datalines;
A B  A C  B C  C H  D E  D F  D G  F E  G I  K L
;

The following statements calculate the connected components and output the results in the data set NodeSetOut:

proc optmodel;
   set<str,str> LINKS;
   read data LinkSetIn into LINKS=[from to];
   set NODES = union {<i,j> in LINKS} {i,j};
   num component{NODES};

   solve with NETWORK /
      links   = (include=LINKS)
      concomp
      out     = (concomp=component)
   ;

   print component;
   create data NodeSetOut from [node] concomp=component;
quit;

The data set NodeSetOut contains the connected components of the input graph and is shown in Figure 9.24.

Figure 9.24: Connected Components of a Simple Undirected Graph

node	concomp
A	1
B	1
C	1
H	1
D	2
E	2
F	2
G	2
I	2
K	3
L	3

Notice that the graph is defined by using only the links array. As seen in Figure 9.23, this graph also contains a singleton node labeled J, which has no associated links. By definition, this node defines its own component. But because the input graph was defined by using only the links array, node J did not show up in the results data set. To define a graph by using nodes that have no associated links, you should also define the input nodes set. In this case, you can define a nodes data set NodeSetIn as follows:

data NodeSetIn;
   input node $ @@;
   datalines;
A  B  C  D  E  F  G  H  I  J  K  L
;

You could also have defined the set directly in PROC OPTMODEL, but in this case, a separate data set nicely preserves the independence between the model and the data.

Now, when you calculate the connected components, you define the input graph by using both the nodes input data set and the links input data set:

proc optmodel;
   set<str,str> LINKS;
   read data LinkSetIn into LINKS=[from to];
   set<str> NODES;
   read data NodeSetIn into NODES=[node];
   num component{NODES};

   solve with NETWORK /
      links   = (include=LINKS)
      nodes   = (include=NODES)
      concomp
      out     = (concomp=component)
   ;

   print component;
   create data NodeSetOut from [node] concomp=component;
quit;

The resulting data set, NodeSetOut, includes the singleton node J as its own component, as shown in Figure 9.25.

Figure 9.25: Connected Components of a Simple Undirected Graph

node	concomp
A	1
B	1
C	1
D	2
E	2
F	2
G	2
H	1
I	2
J	3
K	4
L	4

Connected Components of a Simple Directed Graph

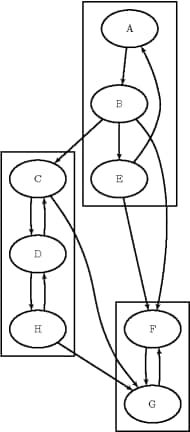
This section illustrates the use of the connected components algorithm on the simple directed graph G that is shown in Figure 9.26.

Figure 9.26: A Simple Directed Graph G

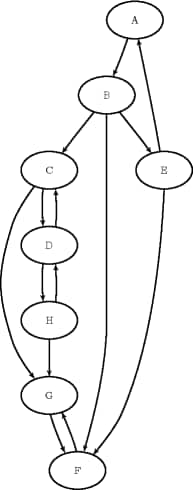
The directed graph G can be represented by the following links data set, LinkSetIn:

data LinkSetIn;
   input from $ to $ @@;
   datalines;
A B  B C  B E  B F  C G
C D  D C  D H  E A  E F
F G  G F  H G  H D
;

The following statements calculate the connected components and output the results in the data set NodeSetOut:

proc optmodel;
   set<str,str> LINKS;
   read data LinkSetIn into LINKS=[from to];
   set NODES = union {<i,j> in LINKS} {i,j};
   num component{NODES};

   solve with NETWORK /
      graph_direction = directed
      links           = (include=LINKS)
      concomp
      out             = (concomp=component)
   ;

   print component;
   create data NodeSetOut from [node] concomp=component;
quit;

The data set NodeSetOut, shown in Figure 9.27, now contains the connected components of the input graph.

Figure 9.27: Connected Components of a Simple Directed Graph

node	concomp
A	3
B	3
C	2
E	3
F	1
G	1
D	2
H	2

The connected components are represented graphically in Figure 9.28.

Figure 9.28: Strongly Connected Components of Graph G