The Network Solver (Experimental)

A spanning tree of a connected undirected graph is a subgraph that is a tree that connects all the nodes together. When weights have been assigned to the links, a minimum spanning tree (MST) is a spanning tree whose sum of link weights is less than or equal to the sum of link weights of every other spanning tree. More generally, any undirected graph (not necessarily connected) has a minimum spanning forest, which is a union of minimum spanning trees of its connected components.

In the network solver, you can invoke the minimum spanning tree algorithm by using the MINSPANTREE option. This algorithm can be used only on undirected graphs.

The resulting minimum spanning tree is contained in the set that is specified in the FOREST= suboption in the OUT= option in the SOLVE WITH NETWORK statement.

The network solver uses Kruskal’s algorithm (Kruskal 1956) to compute the minimum spanning tree. This algorithm runs in time and therefore should scale to very large graphs.

Minimum Spanning Tree for a Simple Undirected Graph

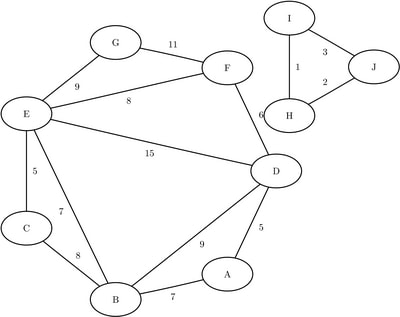
As a simple example, consider the weighted undirected graph in Figure 8.46.

Figure 8.46: A Simple Undirected Graph

The links data set can be represented as follows:

data LinkSetIn;
   input from $ to $ weight @@;
   datalines;
A B  7  A D  5  B C 8  B D 9  B E 7
C E  5  D E 15  D F 6  E F 8  E G 9
F G 11  H I  1  I J 3  H J 2
;

The following statements calculate a minimum spanning forest and output the results in the data set MinSpanForest:

proc optmodel;
   set<str,str> LINKS;
   num weight{LINKS};
   read data LinkSetIn into LINKS=[from to] weight;
   set<str,str> FOREST;

   solve with NETWORK /
      links       = (weight=weight)
      minspantree
      out         = (forest=FOREST)
   ;

   put FOREST;
   create data MinSpanForest from [from to]=FOREST weight;
quit;

The data set MinSpanForest now contains the links that belong to a minimum spanning forest, which is shown in Figure 8.47.

Figure 8.47: Minimum Spanning Forest

from	to	weight
H	I	1
H	J	2
C	E	5
A	D	5
D	F	6
B	E	7
A	B	7
E	G	9
		42

The minimal cost links are shown in green in Figure 8.48.

Figure 8.48: Minimum Spanning Forest

For a more detailed example, see Example 8.5 “Minimum Spanning Tree for Computer Network Topology.”