The Network Solver (Experimental)

Clique

Subsections:

Maximal Cliques of a Simple Undirected Graph

A clique of a graph $G = (N,A)$ is an induced subgraph that is a complete graph. Every node in a clique is connected to every other node in that clique. A maximal clique is a clique that is not a subset of the nodes of any larger clique. That is, it is a set $C$ of nodes such that every pair of nodes in $C$ is connected by a link and every node not in $C$ is missing a link to at least one node in $C$ . The number of maximal cliques in a particular graph can be very large and can grow exponentially with every node added. Finding cliques in graphs has applications in numerous industries including bioinformatics, social networks, electrical engineering, and chemistry.

You can find the maximal cliques of an input graph by invoking the CLIQUE= option. The clique algorithm works only with undirected graphs.

The results for the clique algorithm are written to the set that is specified in the CLIQUES= suboption in the OUT= option. Each node of each clique is listed in the set along with a clique ID (the first argument of the tuple) to identify the clique to which it belongs. A node can appear multiple times in this set if it belongs to multiple cliques.

The algorithm that the network solver uses to compute maximal cliques is a variant of the Bron-Kerbosch algorithm (Bron and Kerbosch, 1973; Harley, 2003). Enumerating all maximal cliques is NP-hard, so this algorithm typically does not scale to very large graphs.

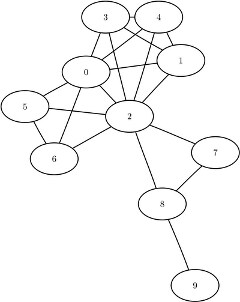
Maximal Cliques of a Simple Undirected Graph

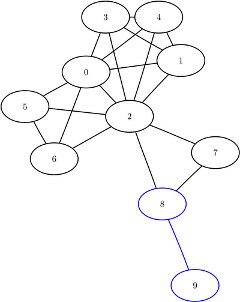
This section illustrates the use of the clique algorithm on the simple undirected graph $G$ that is shown in Figure 8.18.

Figure 8.18: A Simple Undirected Graph $G$

The undirected graph $G$ can be represented by the following links data set LinkSetIn:

data LinkSetIn;
   input from to @@;
   datalines;
0 1  0 2  0 3  0 4  0 5
0 6  1 2  1 3  1 4  2 3
2 4  2 5  2 6  2 7  2 8
3 4  5 6  7 8  8 9
;

The following statements calculate the maximal cliques, output the results in the data set Cliques, and use the CARD function and SLICE operator as a convenient way to compute the clique sizes, which are output to a data set called CliqueSizes:

proc optmodel;
   set<num,num> LINKS;
   read data LinkSetIn into LINKS=[from to];
   set<num,num> CLIQUES;

   solve with NETWORK /
      links  = (include=LINKS)
      clique
      out    = (cliques=CLIQUES)
   ;

   put CLIQUES;
   create data Cliques from [clique node]=CLIQUES;
   num num_cliques = card(setof {<cid,node> in CLIQUES} cid);
   set CLIQUE_IDS = 1..num_cliques;
   num size {cid in CLIQUE_IDS} = card(slice(<cid,*>, CLIQUES));
   create data CliqueSizes from [clique] size;
quit;

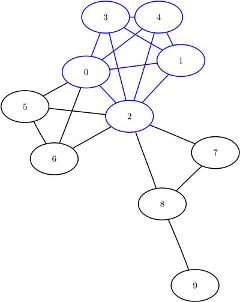
The data set Cliques now contains the maximal cliques of the input graph; it is shown in Figure 8.19.

Figure 8.19: Maximal Cliques of a Simple Undirected Graph

clique	node
1	0
1	2
1	1
1	3
1	4
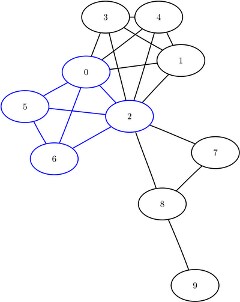
2	0
2	2
2	5
2	6
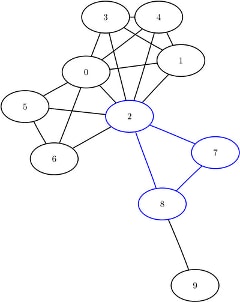
3	2
3	8
3	7
4	8
4	9

In addition, the data set CliqueSizes contains the number of nodes in each clique; it is shown in Figure 8.20.

Figure 8.20: Sizes of Maximal Cliques of a Simple Undirected Graph

clique	size
1	5
2	4
3	3
4	2

The maximal cliques are shown graphically in Figure 8.21 and Figure 8.22.

Figure 8.21: Maximal Cliques $C^1$ and $C^2$

$C^1 = \{ 0,1,2,3,4\}$	$C^2 = \{ 0,2,5,6\}$
$\quad$

Figure 8.22: Maximal Cliques $C^3$ and $C^4$

$C^3 = \{ 2,7,8\}$	$C^4 = \{ 8,9\}$
$\quad$