The INTPOINT Procedure
-
Overview

-
Getting Started

-
Syntax
 Functional SummaryDictionary of OptionsPROC INTPOINT StatementCAPACITY StatementCOEF StatementCOLUMN StatementCOST StatementDEMAND StatementHEADNODE StatementID StatementLO StatementNAME StatementNODE StatementQUIT StatementRHS StatementROW StatementRUN StatementSUPDEM StatementSUPPLY StatementTAILNODE StatementTYPE StatementVAR Statement
Functional SummaryDictionary of OptionsPROC INTPOINT StatementCAPACITY StatementCOEF StatementCOLUMN StatementCOST StatementDEMAND StatementHEADNODE StatementID StatementLO StatementNAME StatementNODE StatementQUIT StatementRHS StatementROW StatementRUN StatementSUPDEM StatementSUPPLY StatementTAILNODE StatementTYPE StatementVAR Statement -
Details
 Input Data SetsOutput Data SetsConverting Any PROC INTPOINT Format to an MPS-Format SAS Data SetCase SensitivityLoop ArcsMultiple ArcsFlow and Value BoundsTightening Bounds and Side ConstraintsReasons for InfeasibilityMissing S Supply and Missing D Demand ValuesBalancing Total Supply and Total DemandHow to Make the Data Read of PROC INTPOINT More EfficientStopping Criteria
Input Data SetsOutput Data SetsConverting Any PROC INTPOINT Format to an MPS-Format SAS Data SetCase SensitivityLoop ArcsMultiple ArcsFlow and Value BoundsTightening Bounds and Side ConstraintsReasons for InfeasibilityMissing S Supply and Missing D Demand ValuesBalancing Total Supply and Total DemandHow to Make the Data Read of PROC INTPOINT More EfficientStopping Criteria -
Examples
 Production, Inventory, Distribution ProblemAltering Arc DataAdding Side ConstraintsUsing Constraints and More Alteration to Arc DataNonarc Variables in the Side ConstraintsSolving an LP Problem with Data in MPS FormatConverting to an MPS-Format SAS Data SetMigration to OPTMODEL: Production, Inventory, Distribution
Production, Inventory, Distribution ProblemAltering Arc DataAdding Side ConstraintsUsing Constraints and More Alteration to Arc DataNonarc Variables in the Side ConstraintsSolving an LP Problem with Data in MPS FormatConverting to an MPS-Format SAS Data SetMigration to OPTMODEL: Production, Inventory, Distribution - References
PROC INTPOINT options ;
This statement invokes the procedure. The following options can be specified in the PROC INTPOINT statement.
This section briefly describes all the input and output data sets used by PROC INTPOINT. The ARCDATA= data set, the NODEDATA= data set, and the CONDATA= data set can contain SAS variables that have special names, for instance _CAPAC_, _COST_, and _HEAD_. PROC INTPOINT looks for such variables if you do not give explicit variable list specifications. If a SAS variable with
a special name is found and that SAS variable is not in another variable list specification, PROC INTPOINT determines that
values of the SAS variable are to be interpreted in a special way. By using SAS variables that have special names, you may
not need to have any variable list specifications.
- ARCDATA=SAS-data-set
-
names the data set that contains arc and, optionally, nonarc variable information and nodal supply/demand data. The ARCDATA= data set must be specified in all PROC INTPOINT statements when solving NPSC problems.
If your problem is an LP, the ARCDATA= data set is optional. You can specify LP variable information such as objective function coefficients, and lower and upper bounds.
- CONDATA=SAS-data-set
-
names the data set that contains the side constraint data. The data set can also contain other data such as arc costs, capacities, lower flow bounds, nonarc variable upper and lower bounds, and objective function coefficients. PROC INTPOINT needs a CONDATA= data set to solve a constrained problem. See the section CONDATA= Data Set for more information.
If your problem is an LP, this data set contains the constraint data, and can also contain other data such as objective function coefficients, and lower and upper bounds. PROC INTPOINT needs a CONDATA= data set to solve an LP.
-
CONOUT=SAS-data-set
COUT=SAS-data-set -
names the output data set that receives an optimal solution. See the section CONOUT= Data Set for more information.
If PROC INTPOINT is outputting observations to the output data set and you want this to stop, press the keys used to stop SAS procedures.
- MPSOUT=SAS-data-set
-
names the SAS data set that contains converted sparse or dense format input data in MPS format. Invoking this option directs the INTPOINT procedure to halt before attempting optimization. For more information about the MPSOUT= option, see the section Converting Any PROC INTPOINT Format to an MPS-Format SAS Data Set. For more information about the MPS-format SAS data set, see Chapter 16: The MPS-Format SAS Data Set in SAS/OR User's Guide: Mathematical Programming.
- NODEDATA=SAS-data-set
-
names the data set that contains the node supply and demand specifications. You do not need observations in the NODEDATA= data set for transshipment nodes. (Transshipment nodes neither supply nor demand flow.) All nodes are assumed to be transshipment nodes unless supply or demand data indicate otherwise. It is acceptable for some arcs to be directed toward supply nodes or away from demand nodes.
This data set is used only when you are solving network problems (not when solving LP problems), in which case the use of the NODEDATA= data set is optional provided that, if the NODEDATA= data set is not used, supply and demand details are specified by other means. Other means include using the MAXFLOW or SHORTPATH option, SUPPLY or DEMAND variable list (or both) in the ARCDATA= data set, and the SOURCE=, SUPPLY=, SINK=, or DEMAND= option in the PROC INTPOINT statement.
The following is a list of options you can use with PROC INTPOINT. The options are listed in alphabetical order.
- ARCS_ONLY_ARCDATA
-
indicates that data for arcs only are in the ARCDATA= data set. When PROC INTPOINT reads the data in the ARCDATA= data set, memory would not be wasted to receive data for nonarc variables. The read might then be performed faster. See the section How to Make the Data Read of PROC INTPOINT More Efficient.
- ARC_SINGLE_OBS
-
indicates that for all arcs and nonarc variables, data for each arc or nonarc variable is found in only one observation of the ARCDATA= data set. When reading the data in the ARCDATA= data set, PROC INTPOINT knows that the data in an observation is for an arc or a nonarc variable that has not had data previously read and that needs to be checked for consistency. The read might then be performed faster.
When solving an LP, specifying the ARC_SINGLE_OBS option indicates that for all LP variables, data for each LP variable is found in only one observation of the ARCDATA= data set. When reading the data in the ARCDATA= data set, PROC INTPOINT knows that the data in an observation is for an LP variable that has not had data previously read and that needs to be checked for consistency. The read might then be performed faster.
If you specify ARC_SINGLE_OBS, PROC INTPOINT automatically works as if GROUPED=ARCDATA is also specified.
See the section How to Make the Data Read of PROC INTPOINT More Efficient.
-
BYPASSDIVIDE=b
BYPASSDIV=b
BPD=b -
should be used only when the MAXFLOW option has been specified; that is, PROC INTPOINT is solving a maximal flow problem. PROC INTPOINT prepares to solve maximal flow problems by setting up a bypass arc. This arc is directed from the SOURCE= to the SINK= and will eventually convey flow equal to INFINITY minus the maximal flow through the network. The cost of the bypass arc must be great enough to drive flow through the network, rather than through the bypass arc. Also, the cost of the bypass arc must be greater than the eventual total cost of the maximal flow, which can be nonzero if some network arcs have nonzero costs. The cost of the bypass is set to the value of the INFINITY= option. Valid values for the BYPASSDIVIDE= option must be greater than or equal to 1.1.
If there are no nonzero costs of arcs in the MAXFLOW problem, the cost of the bypass arc is set to 1.0 (-1.0 if maximizing) if you do not specify the BYPASSDIVIDE= option. The default value for the BYPASSDIVIDE= option (in the presence of nonzero arc costs) is 100.0.
- BYTES=b
-
indicates the size of the main working memory (in bytes) that PROC INTPOINT will allocate. Specifying this option is mandatory. The working memory is used to store all the arrays and buffers used by PROC INTPOINT. If this memory has a size smaller than what is required to store all arrays and buffers, PROC INTPOINT uses various schemes that page information between auxiliary memory (often your machine’s disk) and RAM.
For small problems, specify BYTES=100000. For large problems (those with hundreds of thousands or millions of variables), BYTES=1000000 might do. For solving problems of that size, if you are running on a machine with an inadequate amount of RAM, PROC INTPOINT’s performance will suffer since it will be forced to page or to rely on virtual memory.
If you specify the MEMREP option, PROC INTPOINT will issue messages on the SAS log informing you of its memory usage; that is, how much memory is required to prevent paging, and details about the amount of paging that must be performed, if applicable.
- CON_SINGLE_OBS
-
improves how the CONDATA= data set is read. How it works depends on whether the CONDATA has a dense or sparse format.
If the CONDATA= data set has the dense format, specifying CON_SINGLE_OBS indicates that, for each constraint, data for each can be found in only one observation of the CONDATA= data set.
If the CONDATA= data set has a sparse format, and data for each arc, nonarc variable, or LP variable can be found in only one observation of the CONDATA, then specify the CON_SINGLE_OBS option. If there are
 SAS variables in the ROW and COEF list, then each arc or nonarc can have at most
SAS variables in the ROW and COEF list, then each arc or nonarc can have at most  constraint coefficients in the model. See the section How to Make the Data Read of PROC INTPOINT More Efficient.
constraint coefficients in the model. See the section How to Make the Data Read of PROC INTPOINT More Efficient.
-
DEFCAPACITY=c
DC=c -
requests that the default arc capacity and the default nonarc variable value upper bound (or for LP problems, the default LP variable value upper bound) be c. If this option is not specified, then DEFCAPACITY= INFINITY.
-
DEFCONTYPE=c
DEFTYPE=c
DCT=c -
specifies the default constraint type. This default constraint type is either less than or equal to or is the type indicated by DEFCONTYPE=c. Valid values for this option are
- LE, le, or
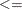
-
for less than or equal to
- EQ, eq, or
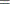
-
for equal to
- GE, ge, or

-
for greater than or equal to
The values do not need to be enclosed in quotes.
- LE, le, or
- DEFCOST=c
-
requests that the default arc cost and the default nonarc variable objective function coefficient (or for an LP, the default LP variable objective function coefficient) be c. If this option is not specified, then DEFCOST=0.0.
-
DEFMINFLOW=m
DMF=m -
requests that the default lower flow bound through arcs and the default lower value bound of nonarc variables (or for an LP, the default lower value bound of LP variables) be m. If a value is not specified, then DEFMINFLOW=0.0.
- DEMAND=d
-
specifies the demand at the SINK node specified by the SINK= option. The DEMAND= option should be used only if the SINK= option is given in the PROC INTPOINT statement and neither the SHORTPATH option nor the MAXFLOW option is specified. If you are solving a minimum cost network problem and the SINK= option is used to identify the sink node, and the DEMAND= option is not specified, then the demand at the sink node is made equal to the network’s total supply.
- GROUPED=grouped
-
PROC INTPOINT can take a much shorter time to read data if the data have been grouped prior to the PROC INTPOINT call. This enables PROC INTPOINT to conclude that, for instance, a new NAME list variable value seen in the ARCDATA= data set grouped by the values of the NAME list variable before PROC INTPOINT was called is new. PROC INTPOINT does not need to check that the NAME has been read in a previous observation. See the section How to Make the Data Read of PROC INTPOINT More Efficient.
-
GROUPED=ARCDATA indicates that the ARCDATA= data set has been grouped by values of the NAME list variable. If
_NAME_is the name of the NAME list variable, you could useproc sort data=arcdata; by _name_;
prior to calling PROC INTPOINT. Technically, you do not have to sort the data, only to ensure that all similar values of the NAME list variable are grouped together. If you specify the ARCS_ONLY_ARCDATA option, PROC INTPOINT automatically works as if GROUPED=ARCDATA is also specified.
-
GROUPED=CONDATA indicates that the CONDATA= data set has been grouped.
If the CONDATA= data set has a dense format, GROUPED=CONDATA indicates that the CONDATA= data set has been grouped by values of the ROW list variable. If
_ROW_is the name of the ROW list variable, you could useproc sort data=condata; by _row_;
prior to calling PROC INTPOINT. Technically, you do not have to sort the data, only to ensure that all similar values of the ROW list variable are grouped together. If you specify the CON_SINGLE_OBS option, or if there is no ROW list variable, PROC INTPOINT automatically works as if GROUPED=CONDATA has been specified.
If the CONDATA= data set has the sparse format, GROUPED=CONDATA indicates that CONDATA has been grouped by values of the COLUMN list variable. If
_COL_is the name of the COLUMN list variable, you could useproc sort data=condata; by _col_;
prior to calling PROC INTPOINT. Technically, you do not have to sort the data, only to ensure that all similar values of the COLUMN list variable are grouped together.
-
GROUPED=BOTH indicates that both GROUPED=ARCDATA and GROUPED=CONDATA are TRUE.
-
GROUPED=NONE indicates that the data sets have not been grouped, that is, neither GROUPED=ARCDATA nor GROUPED=CONDATA is TRUE. This is the default, but it is much better if GROUPED=ARCDATA, or GROUPED=CONDATA, or GROUPED=BOTH.
A data set like
... _XXXXX_ .... bbb bbb aaa ccc cccis a candidate for the GROUPED= option. Similar values are grouped together. When PROC INTPOINT is reading the
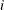 th observation, either the value of the
th observation, either the value of the _XXXXX_variable is the same as the st (that is, the previous observation’s)
st (that is, the previous observation’s) _XXXXX_value, or it is a new_XXXXX_value not seen in any previous observation. This also means that if the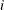 th
th _XXXXX_value is different from the st
st _XXXXX_value, the value of the st
st _XXXXX_variable will not be seen in any observations .
.
-
-
INFINITY=i
INF=i -
is the largest number used by PROC INTPOINT in computations. A number too small can adversely affect the solution process. You should avoid specifying an enormous value for the INFINITY= option because numerical roundoff errors can result. If a value is not specified, then INFINITY=99999999. The INFINITY= option cannot be assigned a value less than 9999.
-
MAXFLOW
MF -
specifies that PROC INTPOINT solve a maximum flow problem. In this case, the PROC INTPOINT procedure finds the maximum flow from the node specified by the SOURCE= option to the node specified by the SINK= option. PROC INTPOINT automatically assigns an INFINITY= option supply to the SOURCE= option node and the SINK= option is assigned the INFINITY= option demand. In this way, the MAXFLOW option sets up a maximum flow problem as an equivalent minimum cost problem.
You can use the MAXFLOW option when solving any flow problem (not necessarily a maximum flow problem) when the network has one supply node (with infinite supply) and one demand node (with infinite demand). The MAXFLOW option can be used in conjunction with all other options (except SHORTPATH, SUPPLY=, and DEMAND=) and capabilities of PROC INTPOINT.
-
MAXIMIZE
MAX -
specifies that PROC INTPOINT find the maximum cost flow through the network. If both the MAXIMIZE and the SHORTPATH options are specified, the solution obtained is the longest path between the SOURCE= and SINK= nodes. Similarly, MAXIMIZE and MAXFLOW together cause PROC INTPOINT to find the minimum flow between these two nodes; this is zero if there are no nonzero lower flow bounds. If solving an LP, specifying the MAXIMIZE option is necessary if you want the maximal optimal solution found instead of the minimal optimum.
- MEMREP
-
indicates that information on the memory usage and paging schemes (if necessary) is reported by PROC INTPOINT on the SAS log.
- NAMECTRL=i
-
is used to interpret arc and nonarc variable names in the CONDATA= data set. In the ARCDATA= data set, an arc is identified by its tail and head node. In the CONDATA= data set, arcs are identified by names. You can give a name to an arc by having a NAME list specification that indicates a SAS variable in the ARCDATA= data set that has names of arcs as values.
PROC INTPOINT requires that arcs that have information about them in the CONDATA= data set have names, but arcs that do not have information about them in the CONDATA= data set can also have names. Unlike a nonarc variable whose name uniquely identifies it, an arc can have several different names. An arc has a default name in the form tail_head, that is, the name of the arc’s tail node followed by an underscore and the name of the arc’s head node.
In the CONDATA= data set, if the dense data format is used (described in the section CONDATA= Data Set), a name of an arc or a nonarc variable is the name of a SAS variable listed in the VAR list specification. If the sparse data format of the CONDATA= data set is used, a name of an arc or a nonarc variable is a value of the SAS variable listed in the COLUMN list specification.
The NAMECTRL= option is used when a name of an arc or a nonarc variable in the CONDATA= data set (either a VAR list variable name or a value of the COLUMN list variable) is in the form tail_head and there exists an arc with these end nodes. If tail_head has not already been tagged as belonging to an arc or nonarc variable in the ARCDATA= data set, PROC INTPOINT needs to know whether tail_head is the name of the arc or the name of a nonarc variable.
If you specify NAMECTRL=1, a name that is not defined in the ARCDATA= data set is assumed to be the name of a nonarc variable. NAMECTRL=2 treats tail_head as the name of the arc with these endnodes, provided no other name is used to associate data in the CONDATA= data set with this arc. If the arc does have other names that appear in the CONDATA= data set, tail_head is assumed to be the name of a nonarc variable. If you specify NAMECTRL=3, tail_head is assumed to be a name of the arc with these end nodes, whether the arc has other names or not. The default value of NAMECTRL is 3.
If the dense format is used for the CONDATA= data set, there are two circumstances that affect how this data set is read:
-
if you are running SAS Version 6, or a previous version to that, or if you are running SAS Version 7 onward and you specify
options validvarname=v6;
in your SAS session. Let’s refer to this as case 1.
-
if you are running SAS Version 7 onward and you do not specify
options validvarname=v6;
in your SAS session. Let’s refer to this as case 2.
For case 1, the SAS System converts SAS variable names in a SAS program to uppercase. The VAR list variable names are uppercased. Because of this, PROC INTPOINT automatically uppercases names of arcs and nonarc variables or LP variables (the values of the NAME list variable) in the ARCDATA= data set. The names of arcs and nonarc variables or LP variables (the values of the NAME list variable) appear uppercased in the CONOUT= data set.
Also, if the dense format is used for the CONDATA= data set, be careful with default arc names (names in the form tailnode_headnode). Node names (values in the TAILNODE and HEADNODE list variables) in the ARCDATA= data set are not automatically uppercased by PROC INTPOINT. Consider the following statements:
data arcdata;
input _from_ $ _to_ $ _name $ ;
datalines;
from to1 .
from to2 arc2
TAIL TO3 .
;
data densecon;
input from_to1 from_to2 arc2 tail_to3;
datalines;
2 3 3 5
;
proc intpoint
arcdata=arcdata condata=densecon;
run;
The SAS System does not uppercase character string values within SAS data sets. PROC INTPOINT never uppercases node names,
so the arcs in observations 1, 2, and 3 in the preceding ARCDATA= data set have the default names from_to1, from_to2, and TAIL_TO3, respectively. When the dense format of the CONDATA= data set is used, PROC INTPOINT does uppercase values of the NAME list variable, so the name of the arc in the second observation of the ARCDATA= data set is ARC2. Thus, the second arc has two names: its default from_to2 and the other that was specified ARC2.
As the SAS System uppercases program code, you must think of the input statement
input from_to1 from_to2 arc2 tail_to3;
as really being
INPUT FROM_TO1 FROM_TO2 ARC2 TAIL_TO3;
The SAS variables named FROM_TO1 and FROM_TO2 are not associated with any of the arcs in the preceding ARCDATA= data set. The values FROM_TO1 and FROM_TO2 are different from all of the arc names from_to1, from_to2, TAIL_TO3, and ARC2. FROM_TO1 and FROM_TO2 could end up being the names of two nonarc variables.
The SAS variable named ARC2 is the name of the second arc in the ARCDATA= data set, even though the name specified in the ARCDATA= data set looks like arc2. The SAS variable named TAIL_TO3 is the default name of the third arc in the ARCDATA= data set.
For case 2, the SAS System does not convert SAS variable names in a SAS program to uppercase.
The VAR list variable names are not uppercased. PROC INTPOINT does not automatically uppercase names of arcs and nonarc variables
or LP variables (the values of the NAME list variable) in the ARCDATA= data set. PROC INTPOINT does not uppercase any SAS variable names, data set values, or indeed anything. Therefore, PROC INTPOINT
respects case, and characters in the data if compared must have the right case if you mean them to be the same. Note how the
input statement in the DATA step that initialized the data set densecon below is specified in the following code:
data arcdata;
input _from_ $ _to_ $ _name $ ;
datalines;
from to1 .
from to2 arc2
TAIL TO3 .
;
data densecon;
input from_to1 from_to2 arc2 TAIL_TO3;
datalines;
2 3 3 5
;
proc intpoint
arcdata=arcdata condata=densecon;
run;
- NARCS=n
-
specifies the approximate number of arcs. See the section How to Make the Data Read of PROC INTPOINT More Efficient.
- NCOEFS=n
-
specifies the approximate number of constraint coefficients. See the section How to Make the Data Read of PROC INTPOINT More Efficient.
- NCONS=n
-
specifies the approximate number of constraints. See the section How to Make the Data Read of PROC INTPOINT More Efficient.
- NNAS=n
-
specifies the approximate number of nonarc variables. See the section How to Make the Data Read of PROC INTPOINT More Efficient.
- NNODES=n
-
specifies the approximate number of nodes. See the section How to Make the Data Read of PROC INTPOINT More Efficient.
- NON_REPLIC=non_replic
-
prevents PROC INTPOINT from doing unnecessary checks of data previously read.
See the section How to Make the Data Read of PROC INTPOINT More Efficient.
- OPTIM_TIMER
-
indicates that the procedure is to issue a message to the SAS log giving the CPU time spent doing optimization. This includes the time spent preprocessing, performing optimization, and postprocessing. Not counted in that time is the rest of the procedure execution, which includes reading the data and creating output SAS data sets.
The time spent optimizing can be small compared to the total CPU time used by the procedure. This is especially true when the problem is quite small (e.g., fewer than 10,000 variables).
- RHSOBS=charstr
-
specifies the keyword that identifies a right-hand-side observation when using the sparse format for data in the CONDATA= data set. The keyword is expected as a value of the SAS variable in the CONDATA= data set named in the COLUMN list specification. The default value of the RHSOBS= option is _RHS_ or _rhs_. If charstr is not a valid SAS variable name, enclose it in quotes.
- SCALE=scale
-
indicates that the NPSC side constraints or the LP constraints are to be scaled. Scaling is useful when some coefficients are either much larger or much smaller than other coefficients. Scaling might make all coefficients have values that have a smaller range, and this can make computations more stable numerically. Try the SCALE= option if PROC INTPOINT is unable to solve a problem because of numerical instability. Specify
-
SCALE=ROW, SCALE=CON, or SCALE=CONSTRAINT if you want the largest absolute value of coefficients in each constraint to be about 1.0
-
SCALE=COL, SCALE=COLUMN, or SCALE=NONARC if you want NPSC nonarc variable columns or LP variable columns to be scaled so that the absolute value of the largest constraint coefficient of that variable is near to 1
-
SCALE=BOTH if you want the largest absolute value of coefficients in each constraint, and the absolute value of the largest constraint coefficient of an NPSC nonarc variable or LP variable to be near to 1. This is the default.
-
-
SHORTPATH
SP -
specifies that PROC INTPOINT solve a shortest path problem. The INTPOINT procedure finds the shortest path between the nodes specified in the SOURCE= option and the SINK= option. The costs of arcs are their lengths. PROC INTPOINT automatically assigns a supply of one flow unit to the SOURCE= node, and the SINK= node is assigned to have a one flow unit demand. In this way, the SHORTPATH option sets up a shortest path problem as an equivalent minimum cost problem.
If a network has one supply node (with supply of one unit) and one demand node (with demand of one unit), you could specify the SHORTPATH option, with the SOURCE= and SINK= nodes, even if the problem is not a shortest path problem. You then should not provide any supply or demand data in the NODEDATA= data set or the ARCDATA= data set.
-
SINK=sinkname
SINKNODE=sinkname -
identifies the demand node. The SINK= option is useful when you specify the MAXFLOW option or the SHORTPATH option and you need to specify toward which node the shortest path or maximum flow is directed. The SINK= option also can be used when a minimum cost problem has only one demand node. Rather than having this information in the ARCDATA= data set or the NODEDATA= data set, use the SINK= option with an accompanying DEMAND= specification for this node. The SINK= option must be the name of a head node of at least one arc; thus, it must have a character value. If the value of the SINK= option is not a valid SAS character variable name (if, for example, it contains embedded blanks), it must be enclosed in quotes.
-
SOURCE=sourcename
SOURCENODE=sourcename -
identifies a supply node. The SOURCE= option is useful when you specify the MAXFLOW or the SHORTPATH option and need to specify from which node the shortest path or maximum flow originates. The SOURCE= option also can be used when a minimum cost problem has only one supply node. Rather than having this information in the ARCDATA= data set or the NODEDATA= data set, use the SOURCE= option with an accompanying SUPPLY= amount of supply at this node. The SOURCE= option must be the name of a tail node of at least one arc; thus, it must have a character value. If the value of the SOURCE= option is not a valid SAS character variable name (if, for example, it contains embedded blanks), it must be enclosed in quotes.
-
SPARSECONDATA
SCDATA -
indicates that the CONDATA= data set has data in the sparse data format. Otherwise, it is assumed that the data are in the dense format.
Note: If the SPARSECONDATA option is not specified, and you are running SAS software Version 6 or you have specified
options validvarname=v6;
all NAME list variable values in the ARCDATA= data set are uppercased. See the section Case Sensitivity.
- SUPPLY=s
-
specifies the supply at the source node specified by the SOURCE= option. The SUPPLY= option should be used only if the SOURCE= option is given in the PROC INTPOINT statement and neither the SHORTPATH option nor the MAXFLOW option is specified. If you are solving a minimum cost network problem and the SOURCE= option is used to identify the source node and the SUPPLY= option is not specified, then by default the supply at the source node is made equal to the network’s total demand.
- THRUNET
-
tells PROC INTPOINT to force through the network any excess supply (the amount by which total supply exceeds total demand) or any excess demand (the amount by which total demand exceeds total supply) as is required. If a network problem has unequal total supply and total demand and the THRUNET option is not specified, PROC INTPOINT drains away the excess supply or excess demand in an optimal manner. The consequences of specifying or not specifying THRUNET are discussed in the section Balancing Total Supply and Total Demand.
- TYPEOBS=charstr
-
specifies the keyword that identifies a type observation when using the sparse format for data in the CONDATA= data set. The keyword is expected as a value of the SAS variable in the CONDATA= data set named in the COLUMN list specification. The default value of the TYPEOBS= option is _TYPE_ or _type_. If charstr is not a valid SAS variable name, enclose it in quotes.
- VERBOSE=v
-
limits the number of similar messages that are displayed on the SAS log.
For example, when reading the ARCDATA= data set, PROC INTPOINT might have cause to issue the following message many times:
ERROR: The HEAD list variable value in obs i in ARCDATA is missing and the TAIL list variable value of this obs is nonmissing. This is an incomplete arc specification.If there are many observations that have this fault, messages that are similar are issued for only the first VERBOSE= such observations. After the ARCDATA= data set has been read, PROC INTPOINT will issue the message
NOTE: More messages similar to the ones immediately above could have been issued but were suppressed as VERBOSE=v.If observations in the ARCDATA= data set have this error, PROC INTPOINT stops and you have to fix the data. Imagine that this error is only a warning and PROC INTPOINT proceeded to other operations such as reading the CONDATA= data set. If PROC INTPOINT finds there are numerous errors when reading that data set, the number of messages issued to the SAS log are also limited by the VERBOSE= option.
When PROC INTPOINT finishes and messages have been suppressed, the message
NOTE: To see all messages, specify VERBOSE=vmin.
is issued. The value of vmin is the smallest value that should be specified for the VERBOSE= option so that all messages are displayed if PROC INTPOINT is run again with the same data and everything else (except VERBOSE=vmin) unchanged.
The default value for the VERBOSE= option is 12.
-
ZERO2=z
Z2=z -
specifies the zero tolerance level used when determining whether the final solution has been reached. ZERO2= is also used when outputting the solution to the CONOUT= data set. Values within z of zero are set to 0.0, where z is the value of the ZERO2= option. Flows close to the lower flow bound or capacity of arcs are reassigned those exact values. If there are nonarc variables, values close to the lower or upper value bound of nonarc variables are reassigned those exact values. When solving an LP problem, values close to the lower or upper value bound of LP variables are reassigned those exact values.
The ZERO2= option works when determining whether optimality has been reached or whether an element in the vector
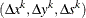 is less than or greater than zero. It is crucial to know that when determining the maximal value for the step length
is less than or greater than zero. It is crucial to know that when determining the maximal value for the step length  in the formula
in the formula
See the description of the PDSTEPMULT= option for more details on this computation.
Two values are deemed to be close if one is within z of the other. The default value for the ZERO2= option is 0.000001. Any value specified for the ZERO2= option that is < 0.0 or > 0.0001 is not valid.
- ZEROTOL=z
-
specifies the zero tolerance used when PROC INTPOINT must compare any real number with another real number, or zero. For example, if
 and
and 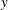 are real numbers, then for
are real numbers, then for  to be considered greater than
to be considered greater than 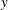 ,
,  must be at least
must be at least  . The ZEROTOL= option is used throughout any PROC INTPOINT run.
. The ZEROTOL= option is used throughout any PROC INTPOINT run.
ZEROTOL=z controls the way PROC INTPOINT performs all double precision comparisons; that is, whether a double precision number is equal to, not equal to, greater than (or equal to), or less than (or equal to) zero or some other double precision number. A double precision number is deemed to be the same as another such value if the absolute difference between them is less than or equal to the value of the ZEROTOL= option.
The default value for the ZEROTOL= option is
 E
E . You can specify the ZEROTOL= option in the INTPOINT statement. Valid values for the ZEROTOL= option must be
. You can specify the ZEROTOL= option in the INTPOINT statement. Valid values for the ZEROTOL= option must be  0.0 and
0.0 and  0.0001. Do not specify a value too close to zero as this defeats the purpose of the ZEROTOL= option. Neither should the value
be too large, as comparisons might be incorrectly performed.
0.0001. Do not specify a value too close to zero as this defeats the purpose of the ZEROTOL= option. Neither should the value
be too large, as comparisons might be incorrectly performed.
- FACT_METHOD=f
-
enables you to choose the type of algorithm used to factorize and solve the main linear systems at each iteration of the interior point algorithm.
FACT_METHOD=LEFT_LOOKING is new for SAS 9.1.2. It uses algorithms described in George, Liu, and Ng (2001). Left looking is one of the main methods used to perform Cholesky optimization and, along with some recently developed implementation approaches, can be faster and require less memory than other algorithms.
Specify FACT_METHOD=USE_OLD if you want the procedure to use the only factorization available prior to SAS 9.1.2.
-
TOLDINF=t
RTOLDINF=t -
specifies the allowed amount of dual infeasibility. In the section Interior Point Algorithmic Details, the vector
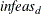 is defined. If all elements of this vector are
is defined. If all elements of this vector are  , the solution is considered dual feasible.
, the solution is considered dual feasible. 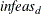 is replaced by a zero vector, making computations faster. This option is the dual equivalent to the TOLPINF= option. Increasing the value of the TOLDINF= option too much can lead to instability, but a modest increase can give the
algorithm added flexibility and decrease the iteration count. Valid values for
is replaced by a zero vector, making computations faster. This option is the dual equivalent to the TOLPINF= option. Increasing the value of the TOLDINF= option too much can lead to instability, but a modest increase can give the
algorithm added flexibility and decrease the iteration count. Valid values for  are greater than
are greater than  E
E . The default is
. The default is  E
E .
.
-
TOLPINF=t
RTOLPINF=t -
specifies the allowed amount of primal infeasibility. This option is the primal equivalent to the TOLDINF= option. In the section Interior Point: Upper Bounds, the vector
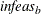 is defined. In the section Interior Point Algorithmic Details, the vector
is defined. In the section Interior Point Algorithmic Details, the vector 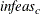 is defined. If all elements in these vectors are
is defined. If all elements in these vectors are  , the solution is considered primal feasible.
, the solution is considered primal feasible. 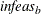 and
and 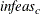 are replaced by zero vectors, making computations faster. Increasing the value of the TOLPINF= option too much can lead to
instability, but a modest increase can give the algorithm added flexibility and decrease the iteration count. Valid values
for
are replaced by zero vectors, making computations faster. Increasing the value of the TOLPINF= option too much can lead to
instability, but a modest increase can give the algorithm added flexibility and decrease the iteration count. Valid values
for  are greater than
are greater than  E
E . The default is
. The default is  E
E .
.
-
TOLTOTDINF=t
RTOLTOTDINF=t -
specifies the allowed total amount of dual infeasibility. In the section Interior Point Algorithmic Details, the vector
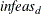 is defined. If
is defined. If  , the solution is considered dual feasible.
, the solution is considered dual feasible. 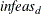 is replaced by a zero vector, making computations faster. This option is the dual equivalent to the TOLTOTPINF= option. Increasing the value of the TOLTOTDINF= option too much can lead to instability, but a modest increase can give the
algorithm added flexibility and decrease the iteration count. Valid values for
is replaced by a zero vector, making computations faster. This option is the dual equivalent to the TOLTOTPINF= option. Increasing the value of the TOLTOTDINF= option too much can lead to instability, but a modest increase can give the
algorithm added flexibility and decrease the iteration count. Valid values for  are greater than
are greater than  E
E . The default is
. The default is  E
E .
.
-
TOLTOTPINF=t
RTOLTOTPINF=t -
specifies the allowed total amount of primal infeasibility. This option is the primal equivalent to the TOLTOTDINF= option. In the section Interior Point: Upper Bounds, the vector
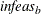 is defined. In the section Interior Point Algorithmic Details, the vector
is defined. In the section Interior Point Algorithmic Details, the vector 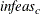 is defined. If
is defined. If  and
and  , the solution is considered primal feasible.
, the solution is considered primal feasible. 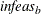 and
and 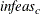 are replaced by zero vectors, making computations faster. Increasing the value of the TOLTOTPINF= option too much can lead
to instability, but a modest increase can give the algorithm added flexibility and decrease the iteration count. Valid values
for
are replaced by zero vectors, making computations faster. Increasing the value of the TOLTOTPINF= option too much can lead
to instability, but a modest increase can give the algorithm added flexibility and decrease the iteration count. Valid values
for  are greater than
are greater than  E
E . The default is
. The default is  E
E .
.
-
CHOLTINYTOL=c
RCHOLTINYTOL=c -
specifies the cut-off tolerance for Cholesky factorization of the
 . If a diagonal value drops below c, the row is essentially treated as dependent and is ignored in the factorization. Valid values for c are between
. If a diagonal value drops below c, the row is essentially treated as dependent and is ignored in the factorization. Valid values for c are between  E
E and
and  E
E . The default value is
. The default value is  E
E .
.
-
DENSETHR=d
RDENSETHR=d -
specifies the density threshold for Cholesky factorization. When the symbolic factorization encounters a column of
 (where
(where  is the remaining unfactorized submatrix) that has DENSETHR= proportion of nonzeros and the remaining part of
is the remaining unfactorized submatrix) that has DENSETHR= proportion of nonzeros and the remaining part of  is at least
is at least  , the remainder of
, the remainder of  is treated as dense. In practice, the lower right part of the Cholesky triangular factor
is treated as dense. In practice, the lower right part of the Cholesky triangular factor  is quite dense and it can be computationally more efficient to treat it as 100% dense. The default value for d is 0.7. A specification of d
is quite dense and it can be computationally more efficient to treat it as 100% dense. The default value for d is 0.7. A specification of d 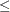 0.0 causes all dense processing; d
0.0 causes all dense processing; d  1.0 causes all sparse processing.
1.0 causes all sparse processing.
-
PDSTEPMULT=p
RPDSTEPMULT=p -
specifies the step-length multiplier. The maximum feasible step-length chosen by the interior point algorithm is multiplied by the value of the PDSTEPMULT= option. This number must be less than 1 to avoid moving beyond the barrier. An actual step-length greater than 1 indicates numerical difficulties. Valid values for p are between 0.01 and 0.999999. The default value is 0.99995.
In the section Interior Point Algorithmic Details, the solution of the next iteration is obtained by moving along a direction from the current iteration’s solution:
![\[ (x^{k+1}, y^{k+1}, s^{k+1}) = (x^ k, y^ k, s^ k) + \alpha (\Delta x^ k, \Delta y^ k, \Delta s^ k) \]](images/ormplpug_intpoint0240.png)
where
 is the maximum feasible step-length chosen by the interior point algorithm. If
is the maximum feasible step-length chosen by the interior point algorithm. If  , then
, then  is reduced slightly by multiplying it by p.
is reduced slightly by multiplying it by p.  is a value as large as possible but
is a value as large as possible but 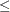 1.0 and not so large that an
1.0 and not so large that an 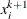 or
or 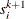 of some variable
of some variable 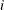 is “too close” to zero.
is “too close” to zero.
-
PRSLTYPE=p
IPRSLTYPE=p -
Preprocessing the linear programming problem often succeeds in allowing some variables and constraints to be temporarily eliminated from the resulting LP that must be solved. This reduces the solution time and possibly also the chance that the optimizer will run into numerical difficulties. The task of preprocessing is inexpensive to do.
You control how much preprocessing to do by specifying PRSLTYPE=p, where p can be –1, 0, 1, 2, or 3:
–1
Do not perform preprocessing. For most problems, specifying PRSLTYPE= –1 is not recommended.
0
Given upper and lower bounds on each variable, the greatest and least contribution to the row activity of each variable is computed. If these are within the limits set by the upper and lower bounds on the row activity, then the row is redundant and can be discarded. Otherwise, whenever possible, the bounds on any of the variables are tightened. For example, if all coefficients in a constraint are positive and all variables have zero lower bounds, then the row’s smallest contribution is zero. If the rhs value of this constraint is zero, then if the constraint type is
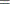 or
or 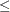 , all the variables in that constraint are fixed to zero. These variables and the constraint are removed. If the constraint
type is
, all the variables in that constraint are fixed to zero. These variables and the constraint are removed. If the constraint
type is  , the constraint is redundant. If the rhs is negative and the constraint is
, the constraint is redundant. If the rhs is negative and the constraint is 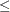 , the problem is infeasible. If just one variable in a row is not fixed, the row to used to impose an implicit upper or lower
bound on the variable and then this row is eliminated. The preprocessor also tries to tighten the bounds on constraint right-hand
sides.
, the problem is infeasible. If just one variable in a row is not fixed, the row to used to impose an implicit upper or lower
bound on the variable and then this row is eliminated. The preprocessor also tries to tighten the bounds on constraint right-hand
sides.
1
When there are exactly two unfixed variables with coefficients in an equality constraint, one variable is solved in terms of the other. The problem will have one less variable. The new matrix will have at least two fewer coefficients and one less constraint. In other constraints where both variables appear, two coefficients are combined into one. PRSLTYPE=0 reductions are also done.
2
It may be possible to determine that an equality constraint is not constraining a variable. That is, if all variables are nonnegative, then
 does not constrain
does not constrain  , since it must be nonnegative if all the
, since it must be nonnegative if all the  ’s are nonnegative. In this case,
’s are nonnegative. In this case,  is eliminated by subtracting this equation from all others containing
is eliminated by subtracting this equation from all others containing  . This is useful when the only other entry for
. This is useful when the only other entry for  is in the objective function. This reduction is performed if there is at most one other nonobjective coefficient. PRSLTYPE=0
reductions are also done.
is in the objective function. This reduction is performed if there is at most one other nonobjective coefficient. PRSLTYPE=0
reductions are also done.
3
All possible reductions are performed. PRSLTYPE=3 is the default.
Preprocessing is iterative. As variables are fixed and eliminated, and constraints are found to be redundant and they too are eliminated, and as variable bounds and constraint right-hand sides are tightened, the LP to be optimized is modified to reflect these changes. Another iteration of preprocessing of the modified LP may reveal more variables and constraints that are eliminated, or tightened.
- PRINTLEVEL2=p
-
is used when you want to see PROC INTPOINT’s progress to the optimum. PROC INTPOINT will produce a table on the SAS log. A row of the table is generated during each iteration and may consist of values of
-
the affine step complementarity
-
the complementarity of the solution for the next iteration
-
the total bound infeasibility
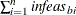 (see the
(see the 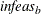 array in the section Interior Point: Upper Bounds)
array in the section Interior Point: Upper Bounds)
-
the total constraint infeasibility
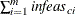 (see the
(see the 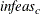 array in the section Interior Point Algorithmic Details)
array in the section Interior Point Algorithmic Details)
-
the total dual infeasibility
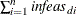 (see the
(see the 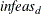 array in the section Interior Point Algorithmic Details)
array in the section Interior Point Algorithmic Details)
As optimization progresses, the values in all columns should converge to zero. If you specify PRINTLEVEL2=2, all columns will appear in the table. If PRINTLEVEL2=1 is specified, only the affine step complementarity and the complementarity of the solution for the next iteration will appear. Some time is saved by not calculating the infeasibility values.
PRINTLEVEL2=2 is specified in all PROC INTPOINT runs in the section Examples: INTPOINT Procedure.
-
- RTTOL=r
-
specifies the zero tolerance used during the ratio test of the interior point algorithm. The ratio test determines
 , the maximum feasible step length.
, the maximum feasible step length.
Valid values for
 are greater than
are greater than  E
E . The default value is
. The default value is  E
E .
.
In the section Interior Point Algorithmic Details, the solution of the next iteration is obtained by moving along a direction from the current iteration’s solution:
![\[ (x^{k+1}, y^{k+1}, s^{k+1}) = (x^ k, y^ k, s^ k) + \alpha (\Delta x^ k, \Delta y^ k, \Delta s^ k) \]](images/ormplpug_intpoint0240.png)
where
 is the maximum feasible step-length chosen by the interior point algorithm. If
is the maximum feasible step-length chosen by the interior point algorithm. If  , then
, then  is reduced slightly by multiplying it by the value of the PDSTEPMULT= option.
is reduced slightly by multiplying it by the value of the PDSTEPMULT= option.  is a value as large as possible but
is a value as large as possible but  and not so large that an
and not so large that an 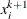 or
or 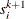 of some variable
of some variable 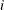 is negative. When determining
is negative. When determining  , only negative elements of
, only negative elements of 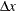 and
and 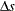 are important.
are important.
RTTOL=
 indicates a number close to zero so that another number
indicates a number close to zero so that another number  is considered truly negative if
is considered truly negative if  . Even though
. Even though  , if
, if  ,
,  may be too close to zero and may have the wrong sign due to rounding error.
may be too close to zero and may have the wrong sign due to rounding error.
-
MAXITERB=m
IMAXITERB=m -
specifies the maximum number of iterations that the interior point algorithm can perform. The default value for m is 100. One of the most remarkable aspects of the interior point algorithm is that for most problems, it usually needs to do a small number of iterations, no matter the size of the problem.
-
PDGAPTOL=p
RPDGAPTOL=p -
specifies the primal-dual gap or duality gap tolerance. Duality gap is defined in the section Interior Point Algorithmic Details. If the relative gap (
 ) between the primal and dual objectives is smaller than the value of the PDGAPTOL= option and both the primal and dual problems
are feasible, then PROC INTPOINT stops optimization with a solution that is deemed optimal. Valid values for p are between
) between the primal and dual objectives is smaller than the value of the PDGAPTOL= option and both the primal and dual problems
are feasible, then PROC INTPOINT stops optimization with a solution that is deemed optimal. Valid values for p are between  E
E and
and  E
E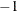 . The default is
. The default is  E
E .
.
- STOP_C=s
-
is used to determine whether optimization should stop. At the beginning of each iteration, if complementarity (the value of the Complem-ity column in the table produced when you specify PRINTLEVEL2=1 or PRINTLEVEL2=2) is
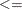 s, optimization will stop. This option is discussed in the section Stopping Criteria.
s, optimization will stop. This option is discussed in the section Stopping Criteria.
- STOP_DG=s
-
is used to determine whether optimization should stop. At the beginning of each iteration, if the duality gap (the value of the Duality_gap column in the table produced when you specify PRINTLEVEL2=1 or PRINTLEVEL2=2) is
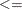 s, optimization will stop. This option is discussed in the section Stopping Criteria.
s, optimization will stop. This option is discussed in the section Stopping Criteria.
- STOP_IB=s
-
is used to determine whether optimization should stop. At the beginning of each iteration, if total bound infeasibility
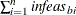 (see the
(see the 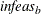 array in the section Interior Point: Upper Bounds; this value appears in the Tot_infeasb column in the table produced when you specify PRINTLEVEL2=1 or PRINTLEVEL2=2) is
array in the section Interior Point: Upper Bounds; this value appears in the Tot_infeasb column in the table produced when you specify PRINTLEVEL2=1 or PRINTLEVEL2=2) is 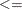 s, optimization will stop. This option is discussed in the section Stopping Criteria.
s, optimization will stop. This option is discussed in the section Stopping Criteria.
- STOP_IC=s
-
is used to determine whether optimization should stop. At the beginning of each iteration, if total constraint infeasibility
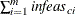 (see the
(see the 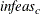 array in the section Interior Point Algorithmic Details; this value appears in the Tot_infeasc column in the table produced when you specify PRINTLEVEL2=2) is
array in the section Interior Point Algorithmic Details; this value appears in the Tot_infeasc column in the table produced when you specify PRINTLEVEL2=2) is 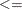 s, optimization will stop. This option is discussed in the section Stopping Criteria.
s, optimization will stop. This option is discussed in the section Stopping Criteria.
- STOP_ID=s
-
is used to determine whether optimization should stop. At the beginning of each iteration, if total dual infeasibility
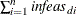 (see the
(see the 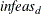 array in the section Interior Point Algorithmic Details; this value appears in the Tot_infeasd column in the table produced when you specify PRINTLEVEL2=2) is
array in the section Interior Point Algorithmic Details; this value appears in the Tot_infeasd column in the table produced when you specify PRINTLEVEL2=2) is 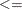 s, optimization will stop. This option is discussed in the section Stopping Criteria.
s, optimization will stop. This option is discussed in the section Stopping Criteria.
- AND_STOP_C=s
-
is used to determine whether optimization should stop. At the beginning of each iteration, if complementarity (the value of the Complem-ity column in the table produced when you specify PRINTLEVEL2=1 or PRINTLEVEL2=2) is
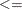 s, and the other conditions related to other AND_STOP parameters are also satisfied, optimization will stop. This option is discussed
in the section Stopping Criteria.
s, and the other conditions related to other AND_STOP parameters are also satisfied, optimization will stop. This option is discussed
in the section Stopping Criteria.
- AND_STOP_DG=s
-
is used to determine whether optimization should stop. At the beginning of each iteration, if the duality gap (the value of the Duality_gap column in the table produced when you specify PRINTLEVEL2=1 or PRINTLEVEL2=2) is
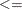 s, and the other conditions related to other AND_STOP parameters are also satisfied, optimization will stop. This option is discussed
in the section Stopping Criteria.
s, and the other conditions related to other AND_STOP parameters are also satisfied, optimization will stop. This option is discussed
in the section Stopping Criteria.
- AND_STOP_IB=s
-
is used to determine whether optimization should stop. At the beginning of each iteration, if total bound infeasibility
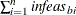 (see the
(see the 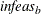 array in the section Interior Point: Upper Bounds; this value appears in the Tot_infeasb column in the table produced when you specify PRINTLEVEL2=1 or PRINTLEVEL2=2) is
array in the section Interior Point: Upper Bounds; this value appears in the Tot_infeasb column in the table produced when you specify PRINTLEVEL2=1 or PRINTLEVEL2=2) is 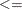 s, and the other conditions related to other AND_STOP parameters are also satisfied, optimization will stop. This option is discussed
in the section Stopping Criteria.
s, and the other conditions related to other AND_STOP parameters are also satisfied, optimization will stop. This option is discussed
in the section Stopping Criteria.
- AND_STOP_IC=s
-
is used to determine whether optimization should stop. At the beginning of each iteration, if total constraint infeasibility
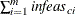 (see the
(see the 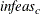 array in the section Interior Point Algorithmic Details; this value appears in the Tot_infeasc column in the table produced when you specify PRINTLEVEL2=2) is
array in the section Interior Point Algorithmic Details; this value appears in the Tot_infeasc column in the table produced when you specify PRINTLEVEL2=2) is 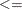 s, and the other conditions related to other AND_STOP parameters are also satisfied, optimization will stop. This option is discussed
in the section Stopping Criteria.
s, and the other conditions related to other AND_STOP parameters are also satisfied, optimization will stop. This option is discussed
in the section Stopping Criteria.
- AND_STOP_ID=s
-
is used to determine whether optimization should stop. At the beginning of each iteration, if total dual infeasibility
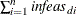 (see the
(see the 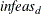 array in the section Interior Point Algorithmic Details; this value appears in the Tot_infeasd column in the table produced when you specify PRINTLEVEL2=2) is
array in the section Interior Point Algorithmic Details; this value appears in the Tot_infeasd column in the table produced when you specify PRINTLEVEL2=2) is 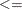 s, and the other conditions related to other AND_STOP parameters are also satisfied, optimization will stop. This option is discussed
in the section Stopping Criteria.
s, and the other conditions related to other AND_STOP parameters are also satisfied, optimization will stop. This option is discussed
in the section Stopping Criteria.
- KEEPGOING_C=s
-
is used to determine whether optimization should stop. When a stopping condition is met, if complementarity (the value of the Complem-ity column in the table produced when you specify PRINTLEVEL2=1 or PRINTLEVEL2=2) is > s, optimization will continue. This option is discussed in the section Stopping Criteria.
- KEEPGOING_DG=s
-
is used to determine whether optimization should stop. When a stopping condition is met, if the duality gap (the value of the Duality_gap column in the table produced when you specify PRINTLEVEL2=1 or PRINTLEVEL2=2) is > s, optimization will continue. This option is discussed in the section Stopping Criteria.
- KEEPGOING_IB=s
-
is used to determine whether optimization should stop. When a stopping condition is met, if total bound infeasibility
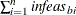 (see the
(see the 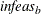 array in the section Interior Point: Upper Bounds; this value appears in the Tot_infeasb column in the table produced when you specify PRINTLEVEL2=1 or PRINTLEVEL2=2) is > s, optimization will continue. This option is discussed in the section Stopping Criteria.
array in the section Interior Point: Upper Bounds; this value appears in the Tot_infeasb column in the table produced when you specify PRINTLEVEL2=1 or PRINTLEVEL2=2) is > s, optimization will continue. This option is discussed in the section Stopping Criteria.
- KEEPGOING_IC=s
-
is used to determine whether optimization should stop. When a stopping condition is met, if total constraint infeasibility
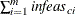 (see the
(see the 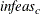 array in the section Interior Point Algorithmic Details; this value appears in the Tot_infeasc column in the table produced when you specify PRINTLEVEL2=2) is > s, optimization will continue. This option is discussed in the section Stopping Criteria.
array in the section Interior Point Algorithmic Details; this value appears in the Tot_infeasc column in the table produced when you specify PRINTLEVEL2=2) is > s, optimization will continue. This option is discussed in the section Stopping Criteria.
- KEEPGOING_ID=s
-
is used to determine whether optimization should stop. When a stopping condition is met, if total dual infeasibility
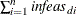 (see the
(see the 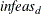 array in the section Interior Point Algorithmic Details; this value appears in the Tot_infeasd column in the table produced when you specify PRINTLEVEL2=2) is > s, optimization will continue. This option is discussed in the section Stopping Criteria.
array in the section Interior Point Algorithmic Details; this value appears in the Tot_infeasd column in the table produced when you specify PRINTLEVEL2=2) is > s, optimization will continue. This option is discussed in the section Stopping Criteria.
- AND_KEEPGOING_C=s
-
is used to determine whether optimization should stop. When a stopping condition is met, if complementarity (the value of the Complem-ity column in the table produced when you specify PRINTLEVEL2=1 or PRINTLEVEL2=2) is > s, and the other conditions related to other AND_KEEPGOING parameters are also satisfied, optimization will continue. This option is discussed in the section Stopping Criteria.
- AND_KEEPGOING_DG=s
-
is used to determine whether optimization should stop. When a stopping condition is met, if the duality gap (the value of the Duality_gap column in the table produced when you specify PRINTLEVEL2=1 or PRINTLEVEL2=2) is > s, and the other conditions related to other AND_KEEPGOING parameters are also satisfied, optimization will continue. This option is discussed in the section Stopping Criteria.
- AND_KEEPGOING_IB=s
-
is used to determine whether optimization should stop. When a stopping condition is met, if total bound infeasibility
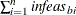 (see the
(see the 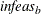 array in the section Interior Point: Upper Bounds; this value appears in the Tot_infeasb column in the table produced when you specify PRINTLEVEL2=2) is > s, and the other conditions related to other AND_KEEPGOING parameters are also satisfied, optimization will continue. This option
is discussed in the section Stopping Criteria.
array in the section Interior Point: Upper Bounds; this value appears in the Tot_infeasb column in the table produced when you specify PRINTLEVEL2=2) is > s, and the other conditions related to other AND_KEEPGOING parameters are also satisfied, optimization will continue. This option
is discussed in the section Stopping Criteria.
- AND_KEEPGOING_IC=s
-
is used to determine whether optimization should stop. When a stopping condition is met, if total constraint infeasibility
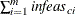 (see the
(see the 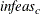 array in the section Interior Point Algorithmic Details; this value appears in the Tot_infeasc column in the table produced when you specify PRINTLEVEL2=2) is > s, and the other conditions related to other AND_KEEPGOING parameters are also satisfied, optimization will continue. This option
is discussed in the section Stopping Criteria.
array in the section Interior Point Algorithmic Details; this value appears in the Tot_infeasc column in the table produced when you specify PRINTLEVEL2=2) is > s, and the other conditions related to other AND_KEEPGOING parameters are also satisfied, optimization will continue. This option
is discussed in the section Stopping Criteria.
- AND_KEEPGOING_ID=s
-
is used to determine whether optimization should stop. When a stopping condition is met, if total dual infeasibility
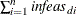 (see the
(see the 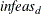 array in the section Interior Point Algorithmic Details; this value appears in the Tot_infeasd column in the table produced when you specify PRINTLEVEL2=2) is > s, and the other conditions related to other AND_KEEPGOING parameters are also satisfied, optimization will continue. This option
is discussed in the section Stopping Criteria.
array in the section Interior Point Algorithmic Details; this value appears in the Tot_infeasd column in the table produced when you specify PRINTLEVEL2=2) is > s, and the other conditions related to other AND_KEEPGOING parameters are also satisfied, optimization will continue. This option
is discussed in the section Stopping Criteria.