Wavelet Analysis
Fourier Transform Infrared (FT-IR) spectroscopy is an important tool in analytic chemistry. The following example demonstrates wavelet analysis applied to an FT-IR spectrum of quartz (Sullivan 2000). The following DATA step creates a data set that contains the spectrum, expressed as an absorbance value for each of 850 wave numbers.
data quartzInfraredSpectrum; WaveNumber=4000.6167786 - _N_ *4.00084378; input Absorbance @@; datalines; 4783 4426 4419 4652 4764 4764 4621 4475 4430 4618 4735 4735 4655 4538 4431 4714 4738 4707 4627 4523 4512 4708 4802 4811 4769 4506 4642 4799 4811 4732 4583 4676 4856 4868 4796 4849 4829 4677 4962 4994 4924 4673 4737 5078 5094 4987 4632 4636 5010 5166 5166 4864 4547 4682 5161 5291 5143 4684 4662 5221 5640 5640 5244 4791 4832 5629 5766 5723 5121 4690 5513 6023 6023 5503 4675 5031 6071 6426 6426 5723 5198 5943 6961 7135 6729 5828 6511 7500 7960 7960 7299 6484 7257 8180 8542 8537 7154 7255 8262 8898 8898 8263 7319 7638 8645 8991 8991 8292 7309 8005 9024 9024 8565 7520 7858 8652 8966 8966 8323 7513 8130 8744 8879 8516 7722 8099 8602 8729 8726 8238 7885 8350 8600 8603 8487 7995 8194 8613 8613 8408 7953 8236 8696 8696 8552 8102 7852 8570 8818 8818 8339 7682 8535 9038 9038 8503 7669 7794 8864 9163 9115 8221 7275 8012 9317 9317 8512 7295 7623 9021 9409 9338 8116 6860 7873 9282 9490 9191 7012 7392 9001 9483 9457 8107 6642 7695 9269 9532 9246 7641 6547 8886 9457 9457 8089 6535 7537 9092 9406 9178 7591 6470 7838 9156 9222 7974 6506 7360 8746 9057 8877 7455 6504 7605 8698 8794 8439 7057 7202 8240 8505 8392 7287 6634 7418 8186 8229 7944 6920 6829 7499 7949 7831 7057 6866 7262 7626 7626 7403 6791 7062 7289 7397 7397 7063 6985 7221 7221 7199 6977 7088 7380 7380 7195 6957 6847 7426 7570 7508 6952 6833 7489 7721 7718 7254 6855 7132 7914 8040 7880 7198 6864 7575 8270 8229 7545 7036 7637 8470 8570 8364 7591 7413 8195 8878 8878 8115 7681 8313 9102 9185 8981 8283 8197 8932 9511 9511 9101 8510 8670 9686 9709 9504 8944 8926 9504 9964 9964 9627 9212 9366 9889 10100 9939 9540 9512 9860 10121 10121 9828 9567 9513 9782 9890 9851 9510 9385 9339 9451 9451 9181 9076 9015 8960 9014 8957 8760 8760 8602 8584 8584 8459 8469 8373 8279 8327 8282 8341 8341 8155 8260 8260 8250 8350 8245 8358 8403 8355 8490 8490 8439 8689 8689 8621 8680 8661 8897 9028 8900 8873 8873 9187 9377 9377 9078 9002 9147 9635 9687 9535 9127 9242 9824 9928 9775 9200 9047 9572 10102 10102 9631 9024 9209 10020 10271 9830 9062 9234 10154 10483 10453 9582 9011 9713 10643 10701 10372 9368 9857 10865 10936 10572 9574 9691 10820 11452 11452 10623 9903 10787 11931 12094 11302 10604 11458 12608 12808 12589 11629 11795 12863 13575 13575 12968 12498 13268 14469 14469 13971 13727 14441 15334 15515 15410 14986 15458 16208 16722 16722 16618 17061 17661 18089 18089 18184 18617 19015 19467 19633 19830 20334 20655 20947 21347 21756 22350 22584 22736 22986 23412 24126 24498 24501 24598 24986 25729 26356 26356 26271 26754 27624 28162 28162 28028 28305 29223 30073 30219 30185 30308 31831 32699 32819 32793 33320 34466 35600 36038 36086 36518 37517 38765 39462 39681 40209 41243 42274 42772 42876 43172 43929 44842 45351 45395 45551 46035 46774 47353 47353 47362 47908 48539 48936 48978 49057 49497 50101 50670 50914 51134 51603 52276 53007 53399 53769 54281 54815 54914 55365 55874 56180 56272 56669 57076 57422 57458 57525 57681 57679 57318 57318 57181 57417 57409 57144 57047 56377 56551 56483 56098 56034 55598 55364 55364 55146 54904 54990 55501 55533 55362 54387 55340 55240 54748 53710 55346 55795 55795 55060 55945 55945 55753 56759 56859 57509 56741 56273 56961 58566 58566 58104 59275 59275 59051 59090 59461 60362 60560 61103 61272 61380 61878 62067 62237 62214 61182 61532 62173 62253 60473 61346 63143 63378 61519 61753 63078 63841 63841 62115 61227 63237 63237 61338 63951 63951 63604 63633 64625 65135 64976 63630 63494 63834 63338 63218 62324 64131 64234 65122 64551 64127 64415 64621 64621 63142 65344 65585 65476 65074 64714 63803 65085 65085 65646 65646 64851 65390 65390 64997 65541 65587 65682 65952 65952 65390 65702 65846 65734 65734 65628 65509 65571 65636 65636 65620 65487 65544 65547 65738 65758 65711 65360 65362 65362 65231 65333 65453 65473 65435 65302 65412 65412 65351 65242 65242 65170 65221 65297 65297 65202 65177 65183 65184 65179 65209 65209 65144 65134 65113 65009 64919 64945 64988 64988 64856 64686 64529 64370 64282 64233 64169 63869 63685 63480 63373 63349 63307 63131 63017 62885 62736 62736 62706 62666 62622 62671 62781 62853 62950 63106 63135 63141 63220 63263 63489 63807 63966 64132 64294 64612 64841 64985 65159 65204 65259 65540 65707 65749 65732 65719 65820 65895 65925 65925 65888 65937 66059 66109 66109 66078 66007 65897 65897 65747 65490 64947 64598 64363 64140 63801 63571 63395 63333 63442 63442 63339 63196 62911 62118 61795 61454 61456 61607 62025 62190 62190 62023 61780 61502 61482 61458 61320 61015 60852 60708 60684 60522 60488 60506 60640 60797 60995 61141 61141 61036 60664 60522 60017 59681 59129 58605 58035 57192 56137 54995 53586 52037 50283 48565 45419 43341 41111 36131 35377 34431 31679 29237 26898 24655 22417 19876 17244 15176 12575 10532 8180 6040 4059 2210 575 ;
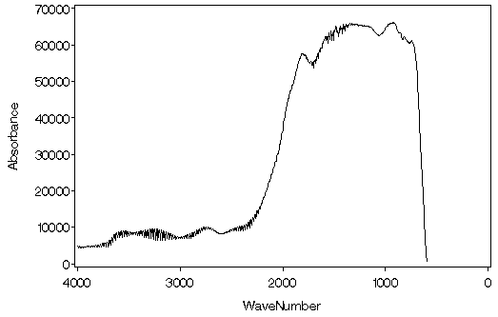
The following statements produce the line plot of these data displayed in Figure 20.1.
symbol1 c=black i=join v=none;
proc gplot data=quartzInfraredSpectrum;
plot Absorbance*WaveNumber/
hminor = 0 vminor = 0
vaxis = axis1
hreverse frame;
axis1 label = ( r=0 a=90 );
run;
These data contain information at two distinct scales, namely a low-frequency curve superimposed with a high-frequency oscillation.
Notice that the oscillation is not uniform but occurs in several distinct bands. Wavelet analysis is an appropriate tool for
providing insight into this type of data, as it enables you to identify the frequencies present in the absorbance data as
the wave number changes. This property of wavelets is known as “time frequency localization”; in this case the role of time is played by WaveNumber. Also note that the dependent variable Absorbance is measured at equally spaced values of the independent variable WaveNumber. This condition is necessary for the direct use of the discrete wavelet transform that is implemented in the SAS/IML wavelet
functions.