MAD Function :: SAS/IML(R) 13.1 User's Guide

Previous Page|Next Page

MAD Function

Subsections:

Example

MAD (x <, method> ) ;

The MAD function computes the univariate (scaled) median absolute deviation of each column of the input matrix.

The arguments to the MAD function are as follows:

x

is an 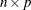$n \times p$ input data matrix.

method

is an optional string argument with the following values:

“MAD”: for computing the median absolute deviation (MAD); this is the default.
“NMAD”: for computing the normalized version of MAD
“SN”: for computing $S_ n$
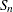
“QN”: for computing $Q_ n$

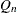
For simplicity, the following descriptions assume that the input argument x is a column vector. The notation $x_ i$ means the $i$ th element of the column vector x.

The MAD function can be used for computing one of the following three robust scale estimates:

median absolute deviation (MAD) or normalized form of MAD,

$\mbox{MAD}_ n = b * med_ i^ n \; |x_ i - med_ j^ n \; x_ j|$

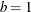where $b=1$ is the unscaled default and 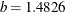$b=1.4826$ is used for the scaled version (consistency with the Gaussian distribution).
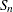$S_ n$ , which is a more efficient alternative to MAD,

$S_ n = c_ n * med_ i \; med_{j \neq i} \; |x_ i - x_ j|$

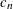where the outer median is a low median (order statistic of rank $\left[\frac{n+1}{2}\right]$ ) and the inner median is a high median (order statistic of rank $\left[\frac{n}{2}+1\right]$ ), and where $c_ n$ is a scalar that depends on sample size $n$ .
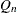$Q_ n$ is another efficient alternative to MAD. It is based on the 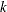$k$ th-order statistic of the 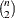${n \choose 2}$ inter-point distances,

$Q_ n = d_ n * \{ |x_ i - x_ j|; \quad i < j \} _{(k)} \quad \mbox{with} \quad k \approx {n \choose 2}/ 4$

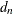where $d_ n$ is a scalar similar to but different from 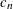$c_ n$ . See Rousseeuw and Croux (1993) for more details.

The scalars $c_ n$ and $d_ n$ are defined as follows:

$c_ n = 1.1926 * \left\{ \begin{array}{ll} 0.743 & \mbox{for n=2} \\ 1.851 & \mbox{for n=3} \\ 0.954 & \mbox{for n=4} \\ 1.351 & \mbox{for n=5} \\ 0.993 & \mbox{for n=6} \\ 1.198 & \mbox{for n=7} \\ 1.005 & \mbox{for n=8} \\ 1.131 & \mbox{for n=9} \\ n/(n - 0.9) & \mbox{for other odd n} \\ 1.0 & \mbox{otherwise} \end{array} \right. \qquad d_ n = 2.2219 * \left\{ \begin{array}{ll} 0.399 & \mbox{for n=2} \\ 0.994 & \mbox{for n=3} \\ 0.512 & \mbox{for n=4} \\ 0.844 & \mbox{for n=5} \\ 0.611 & \mbox{for n=6} \\ 0.857 & \mbox{for n=7} \\ 0.669 & \mbox{for n=8} \\ 0.872 & \mbox{for n=9} \\ n/(n + 1.4) & \mbox{for other odd n} \\ n/(n + 3.8) & \mbox{otherwise} \end{array} \right. \qquad$

Example

The following example uses the univariate data set of Barnett and Lewis (1978). The data set is used in Chapter 12 to illustrate the univariate LMS and LTS estimates.

 b = {3, 4, 7, 8, 10, 949, 951};

 rmad1 = mad(b);
 rmad2 = mad(b,"mad");
 rmad3 = mad(b,"nmad");
 rmad4 = mad(b,"sn");
 rmad5 = mad(b,"qn");
 print "Default MAD=" rmad1,
       "Common MAD =" rmad2,
       "MAD*1.4826 =" rmad3,
       "Robust S_n =" rmad4,
       "Robust Q_n =" rmad5;

Figure 24.201: Median Absolute Deviations

	rmad1
Default MAD=	4

	rmad2
Common MAD =	4

	rmad3
MAD*1.4826 =	5.9304089

	rmad4
Robust S_n =	7.143674

	rmad5
Robust Q_n =	5.7125049