The LUPDT subroutine provides updating and downdating for rank deficient linear least squares solutions, complete orthogonal factorization, and Moore-Penrose inverses.
The LUPDT subroutine returns the following values:
- lup
-
is an
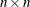 lower triangular matrix
lower triangular matrix  that is updated or downdated by using the
that is updated or downdated by using the 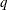 rows in
rows in 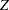 .
.
- bup
-
is an
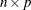 matrix
matrix 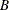 of right-hand sides that is updated or downdated by using the
of right-hand sides that is updated or downdated by using the 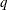 rows in
rows in 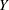 . If b is not specified, bup is not accessible.
. If b is not specified, bup is not accessible.
- sup
-
is a
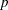 vector of square roots of residual sum of squares that is updated or downdated by using the
vector of square roots of residual sum of squares that is updated or downdated by using the 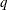 rows in
rows in 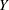 . If ssq is not specified, sup is not accessible.
. If ssq is not specified, sup is not accessible.
The input arguments to the LUPDT subroutine are as follows:
- L
-
specifies an
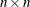 lower triangular matrix
lower triangular matrix  to be updated or downdated by
to be updated or downdated by 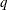 row vectors
row vectors  stored in the
stored in the 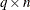 matrix
matrix 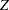 . Only the lower triangle of L is used; the upper triangle can contain any information.
. Only the lower triangle of L is used; the upper triangle can contain any information.
- z
-
is a
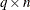 matrix
matrix 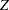 used rowwise to update or downdate the matrix
used rowwise to update or downdate the matrix  .
.
- b
-
specifies an optional
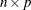 matrix
matrix 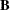 of right-hand sides that have to be updated or downdated simultaneously with L. If b is specified, the argument y must be specified.
of right-hand sides that have to be updated or downdated simultaneously with L. If b is specified, the argument y must be specified.
- y
-
specifies an optional
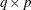 matrix
matrix 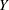 used rowwise to update or downdate the right-hand-side matrix b.
used rowwise to update or downdate the right-hand-side matrix b.
- ssq
-
specifies an optional
 vector that, if b is specified, specifies the square root of the error sum of squares that should be updated or downdated simultaneously with
L and b.
vector that, if b is specified, specifies the square root of the error sum of squares that should be updated or downdated simultaneously with
L and b.
The relevant formula for the LUPDT call is ![]() . See the section Complete QR Decomposition with LUPDT in the documentation for the RZLIND call.
. See the section Complete QR Decomposition with LUPDT in the documentation for the RZLIND call.