The LAV subroutine performs linear least absolute value regression by solving the ![]() norm minimization problem.
norm minimization problem.
The LAV subroutine returns the following values:
- rc
-
is a scalar return code that indicates the reason for optimization termination.
rc
Termination
0
Successful
1
Successful, but approximate covariance matrix and standard errors cannot be computed
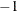 or
or 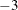
Unsuccessful: error in the input arguments
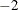
Unsuccessful: matrix
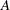 is rank-deficient (
is rank-deficient (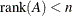 )
)
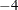
Unsuccessful: maximum iteration limit exceeded
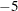
Unsuccessful: no solution found for ill-conditioned problem
- xr
-
specifies a vector or matrix with
 columns. If the optimization process is not successfully completed, xr is a row vector with
columns. If the optimization process is not successfully completed, xr is a row vector with  missing values. If termination is successful and the opt[3] option is not set, xr is the vector with the optimal estimate,
missing values. If termination is successful and the opt[3] option is not set, xr is the vector with the optimal estimate, 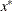 . If termination is successful and the opt[3] option is specified, xr is an
. If termination is successful and the opt[3] option is specified, xr is an 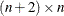 matrix that contains the optimal estimate,
matrix that contains the optimal estimate, 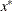 , in the first row, the asymptotic standard errors in the second row, and the
, in the first row, the asymptotic standard errors in the second row, and the 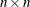 covariance matrix of parameter estimates in the remaining rows.
covariance matrix of parameter estimates in the remaining rows.
The input arguments to the LAV subroutine are as follows:
- a
-
specifies an
 matrix
matrix 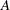 with
with 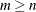 and full column rank,
and full column rank, 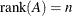 . If you want to include an intercept in the model, you must include a column of ones in the matrix
. If you want to include an intercept in the model, you must include a column of ones in the matrix 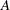 .
.
- b
-
specifies the
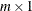 vector
vector 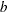 .
.
- x0
-
specifies an optional
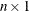 vector that specifies the starting point of the optimization.
vector that specifies the starting point of the optimization.
- opt
-
is an optional vector used to specify options. If an element of the opt vector is missing, the default value is used.
-
opt[1] specifies the maximum number maxi of outer iterations (this corresponds to the number of changes of the Huber parameter
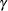 ). The default is
). The default is 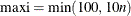 . (The number of inner iterations is restricted by an internal threshold. If the number of inner iterations exceeds this threshold,
a new outer iteration is started with an increased value of
. (The number of inner iterations is restricted by an internal threshold. If the number of inner iterations exceeds this threshold,
a new outer iteration is started with an increased value of 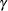 .)
.)
-
opt[2] specifies the amount of printed output. Higher values request additional output and include the output of lower values.
opt[2]
Termination
0
No output is printed.
1
Error and warning messages are printed.
2
The iteration history is printed (this is the default).
3
The
 least squares (
least squares (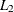 norm) estimates are printed if no starting point is specified, the
norm) estimates are printed if no starting point is specified, the 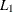 norm estimates are always printed, and if opt[3] is set, the estimates are printed together with the asymptotic standard errors.
norm estimates are always printed, and if opt[3] is set, the estimates are printed together with the asymptotic standard errors.
4
The
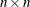 approximate covariance matrix of parameter estimates is printed if opt[3] is set.
approximate covariance matrix of parameter estimates is printed if opt[3] is set.
5
The residual and predicted values for all
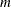 rows (equations) of
rows (equations) of 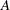 are printed.
are printed.
-
opt[3] specifies which estimate of the variance of the median of nonzero residuals be used as a factor for the approximate covariance matrix of parameter estimates and for the approximate standard errors (ASE). If opt[3]
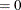 , the McKean-Schrader (1987) estimate is used, and if opt[3]
, the McKean-Schrader (1987) estimate is used, and if opt[3]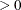 , the Cox-Hinkley (1974) estimate, with
, the Cox-Hinkley (1974) estimate, with 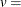 opt[3], is used. The default behavior is that the covariance matrix is not computed.
opt[3], is used. The default behavior is that the covariance matrix is not computed.
-
opt[4] specifies whether a computationally expensive test for necessary and sufficient optimality of the solution
 is executed. The default behavior (opt[4]
is executed. The default behavior (opt[4]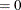 ) is that the convergence test is not performed.
) is that the convergence test is not performed.
-
Missing values are not permitted in the a or b argument. The ![]() argument is ignored if it contains any missing values. Missing values in the opt argument cause the default value to be used.
argument is ignored if it contains any missing values. Missing values in the opt argument cause the default value to be used.
The LAV subroutine is designed for solving the unconstrained linear ![]() norm minimization problem,
norm minimization problem,
for ![]() equations with
equations with ![]() (unknown) parameters
(unknown) parameters ![]() . This is equivalent to estimating the unknown parameter vector,
. This is equivalent to estimating the unknown parameter vector, ![]() , by least absolute value regression in the model
, by least absolute value regression in the model
where ![]() is the vector of
is the vector of ![]() observations,
observations, ![]() is the design matrix, and
is the design matrix, and ![]() is a random error term.
is a random error term.
An algorithm by Madsen and Nielsen (1993) is used, which can be faster for large values of ![]() and
and ![]() than the Barrodale and Roberts (1974) algorithm. The current version of the algorithm assumes that
than the Barrodale and Roberts (1974) algorithm. The current version of the algorithm assumes that ![]() has full column rank. Also, constraints cannot be imposed on the parameters in this version.
has full column rank. Also, constraints cannot be imposed on the parameters in this version.
The ![]() norm minimization problem is more difficult to solve than the least squares (
norm minimization problem is more difficult to solve than the least squares (![]() norm) minimization problem because the objective function of the
norm) minimization problem because the objective function of the ![]() norm problem is not continuously differentiable (the first derivative has jumps). A function that is continuous but not continuously
differentiable is called nonsmooth. By using PROC NLP and the nonlinear optimization subroutines, you can obtain the estimates in linear and nonlinear
norm problem is not continuously differentiable (the first derivative has jumps). A function that is continuous but not continuously
differentiable is called nonsmooth. By using PROC NLP and the nonlinear optimization subroutines, you can obtain the estimates in linear and nonlinear ![]() norm estimation (even subject to linear or nonlinear constraints) as long as the number of parameters,
norm estimation (even subject to linear or nonlinear constraints) as long as the number of parameters, ![]() , is small. Using the nonlinear optimization subroutines, there are two ways to solve the nonlinear
, is small. Using the nonlinear optimization subroutines, there are two ways to solve the nonlinear ![]() norm,
norm, ![]() , problem:
, problem:
-
For small values of
 , you can implement the Nelder-Mead simplex algorithm with the NLPNMS subroutine to solve the minimization problem in its original specification. The Nelder-Mead simplex algorithm does not assume a smooth
objective function, does not take advantage of any derivatives, and therefore does not require continuous differentiability
of the objective function. See the section NLPNMS Call for details.
, you can implement the Nelder-Mead simplex algorithm with the NLPNMS subroutine to solve the minimization problem in its original specification. The Nelder-Mead simplex algorithm does not assume a smooth
objective function, does not take advantage of any derivatives, and therefore does not require continuous differentiability
of the objective function. See the section NLPNMS Call for details.
-
Gonin and Money (1989) describe how an original
 norm estimation problem can be modified to an equivalent optimization problem with nonlinear constraints which has a simple
differentiable objective function. You can invoke the NLPQN subroutine, which implements a quasi-Newton algorithm, to solve the nonlinearly constrained
norm estimation problem can be modified to an equivalent optimization problem with nonlinear constraints which has a simple
differentiable objective function. You can invoke the NLPQN subroutine, which implements a quasi-Newton algorithm, to solve the nonlinearly constrained  norm optimization problem. See the section NLPQN Call for details about the NLPQN subroutine.
norm optimization problem. See the section NLPQN Call for details about the NLPQN subroutine.
Both approaches are successful only for a small number of parameters and good initial estimates. If you cannot supply good
initial estimates, the optimal results of the corresponding nonlinear least squares (![]() norm) estimation can provide fairly good initial estimates.
norm) estimation can provide fairly good initial estimates.
Gonin and Money (1989) show that the nonlinear ![]() norm estimation problem
norm estimation problem
can be reformulated as a linear optimization problem with nonlinear constraints in the following ways.
-
as a linear optimization problem with
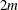 nonlinear inequality constraints in
nonlinear inequality constraints in 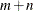 variables
variables 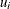 and
and 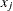 ,
,
![\[ \min _{x} \sum _{i=1}^ m u_ i \mbox{ subject to } \left. \begin{array}{lcr} f_ i(x) - u_ i & \leq & 0 \\ f_ i(x) + u_ i & \geq & 0 \\ u_ i & \geq & 0 \end{array} \right\} \quad i=1,\ldots ,m \]](images/imlug_langref0725.png)
-
as a linear optimization problem with
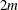 nonlinear equality constraints in
nonlinear equality constraints in 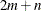 variables
variables 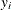 ,
,  , and
, and 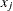 ,
,
![\[ \min _{x} \sum _{i=1}^ m (y_ i + z_ i) \mbox{ subject to } \left. \begin{array}{lcr} f_ i(x) + y_ i - z_ i & = & 0 \\ y_ i & \geq & 0 \\ z_ i & \geq & 0 \end{array} \right\} \quad i=1,\ldots ,m \]](images/imlug_langref0729.png)
For linear functions ![]() ,
, ![]() , you obtain linearly constrained linear optimization problems, for which the number of variables and constraints is on the
order of the number of observations,
, you obtain linearly constrained linear optimization problems, for which the number of variables and constraints is on the
order of the number of observations, ![]() . The advantage that the algorithm by Madsen and Nielsen (1993) has over the Barrodale and Roberts (1974) algorithm is that its computational cost increases only linearly with
. The advantage that the algorithm by Madsen and Nielsen (1993) has over the Barrodale and Roberts (1974) algorithm is that its computational cost increases only linearly with ![]() , and it can be faster for large values of
, and it can be faster for large values of ![]() .
.
In addition to computing an optimal solution ![]() that minimizes
that minimizes ![]() , you can also compute approximate standard errors and the approximate covariance matrix of
, you can also compute approximate standard errors and the approximate covariance matrix of ![]() . The standard errors can be used to compute confidence limits.
. The standard errors can be used to compute confidence limits.
The following example is the same one used for illustrating the LAV subroutine by Lee and Gentle (1986). ![]() and
and ![]() are as follows:
are as follows:
![\[ A = \left[ \begin{array}{rr} 1 & 0 \\ 1 & 1 \\ 1 & -1 \\ 1 & -1 \\ 1 & 2 \\ 1 & 2 \end{array} \right] b = \left[ \begin{array}{r} 1 \\ 2 \\ 1 \\ -1 \\ 2 \\ 4 \end{array} \right] \]](images/imlug_langref0733.png)
The following statements specify the matrix ![]() , the vector
, the vector ![]() , and the options vector opt. The options vector specifies that all output is printed (opt[2]
, and the options vector opt. The options vector specifies that all output is printed (opt[2]![]() ), that the asymptotic standard errors and covariance matrix are computed based on the McKean-Schrader (1987) estimate
), that the asymptotic standard errors and covariance matrix are computed based on the McKean-Schrader (1987) estimate ![]() of the variance of the median (opt[3]
of the variance of the median (opt[3]![]() ), and that the convergence test be performed (opt[4]
), and that the convergence test be performed (opt[4]![]() ).
).
a = { 0, 1, -1, -1, 2, 2 };
m = nrow(a);
a = j(m, 1, 1.) || a;
b = { 1, 2, 1, -1, 2, 4 };
opt= { . 5 0 1 };
call lav(rc, xr, a, b, , opt);
The first part of the output is shown in Figure 24.183. This output displays the least squares solution, which is used as the starting point. The estimates of the largest and smallest
nonzero eigenvalues of ![]() give only an idea of the magnitude of these values, and they can be very crude approximations.
give only an idea of the magnitude of these values, and they can be very crude approximations.
The second part of the printed output shows the iteration history. It is shown in Figure 24.184.
Figure 24.184: Iteration History
| LAV (L1) Estimation | ||||||
|---|---|---|---|---|---|---|
| Start with LS Solution | ||||||
| Start Iter: gamma=1 ActEqn=6 | ||||||
| Iter | N Huber | Act Eqn | Rank | Gamma | L1(x) | F(Gamma) |
| 1 | 1 | 2 | 2 | 0.9000 | 4.000000 | 2.200000 |
| 1 | 1 | 2 | 2 | 0.0000 | 4.000000 | 2.200000 |
The third part of the output is shown in Figure 24.185. This output displays the ![]() norm solution (first row) together with asymptotic standard errors (second row) and the asymptotic covariance matrix of parameter
estimates. The ASEs are the square roots of the diagonal elements of this covariance matrix.
norm solution (first row) together with asymptotic standard errors (second row) and the asymptotic covariance matrix of parameter
estimates. The ASEs are the square roots of the diagonal elements of this covariance matrix.
Figure 24.185: Parameter and Covariance Estimates
| L1 Solution with ASE | ||
|---|---|---|
| Est | 1 | 1 |
| ASE | 0.4482711811 | 0.3310702082 |
| Cov Matrix: McKean-Schrader | |
|---|---|
| 0.2009470518 | -0.054803741 |
| -0.054803741 | 0.1096074828 |
The last part of the printed output shows the predicted values and residuals, as in Lee and Gentle (1986). It is shown in Figure 24.186.
Figure 24.186: Predicted and Residual Values
| Predicted Values and Residuals | |||
|---|---|---|---|
| N | Observed | Predicted | Residual |
| 1 | 1.0000 | 1.0000 | 0 |
| 2 | 2.0000 | 2.0000 | 0 |
| 3 | 1.0000 | 0.0000 | 1.000000 |
| 4 | -1.0000 | 0.0000 | -1.000000 |
| 5 | 2.0000 | 3.0000 | -1.000000 |
| 6 | 4.0000 | 3.0000 | 1.000000 |