The NLPNMS subroutine use the Nelder-Mead simplex method to compute an optimum value of a function.
See the section Nonlinear Optimization and Related Subroutines for a listing of all NLP subroutines. See Chapter 14 for a description of the arguments of NLP subroutines.
The Nelder-Mead simplex method is one of the subroutines that can solve optimization problems with nonlinear constraints.
It does not use any derivatives, and it does not assume that the objective function has continuous derivatives. However, the
objective function must be continuous. The NLPNMS technique uses a large number of function calls, and it can be unable to
generate precise results when ![]() .
.
The NLPNMS subroutine uses the following simplex algorithms:
-
For unconstrained or only boundary-constrained problems, the original Nelder-Mead simplex algorithm is implemented and extended to boundary constraints. This algorithm does not compute the objective for infeasible points, and it is invoked if the “nlc” module argument is not specified and the blc argument contains at most two rows (corresponding to lower and upper bounds).
-
For linearly or nonlinearly constrained problems, a slightly modified version of Powell’s (1992) constrained optimization by linear approximations (COBYLA) implementation is used. This algorithm is invoked if the “nlc” module argument is specified or if at least one linear constraint is specified with the blc argument.
The original Nelder-Mead algorithm cannot be used for general linear or nonlinear constraints, but in the unconstrained or boundary-constrained cases, it can be faster. It changes the shape of the simplex by adapting the nonlinearities of the objective function; this contributes to an increased speed of convergence.
Powell’s COBYLA algorithm is a sequential trust-region algorithm that tries to maintain a regularly shaped simplex throughout
the iterations. The algorithm uses a monotone-decreasing radius, ![]() , of a spheric trust region. The modification implemented in the NLPNMS call permits an increase of the trust-region radius
, of a spheric trust region. The modification implemented in the NLPNMS call permits an increase of the trust-region radius
![]() in special situations. A sequence of iterations is performed with a constant trust-region radius
in special situations. A sequence of iterations is performed with a constant trust-region radius ![]() until the computed function reduction is much less than the predicted reduction. Then, the trust-region radius
until the computed function reduction is much less than the predicted reduction. Then, the trust-region radius ![]() is reduced. The trust-region radius is increased only if the computed function reduction is relatively close to the predicted
reduction and if the simplex is well-shaped. The start radius,
is reduced. The trust-region radius is increased only if the computed function reduction is relatively close to the predicted
reduction and if the simplex is well-shaped. The start radius, ![]() , can be specified with the second element of the par argument, and the final radius,
, can be specified with the second element of the par argument, and the final radius, ![]() , can be specified with the ninth element of the tc argument. Convergence to small values of
, can be specified with the ninth element of the tc argument. Convergence to small values of ![]() , or high-precision convergence, can require many calls of the function and constraint modules and can result in numerical
problems. The main reasons for the slow convergence of the COBYLA algorithm are as follows:
, or high-precision convergence, can require many calls of the function and constraint modules and can result in numerical
problems. The main reasons for the slow convergence of the COBYLA algorithm are as follows:
-
Linear approximations of the objective and constraint functions are used locally.
-
Maintaining the regularly shaped simplex and not adapting its shape to nonlinearities yields very small simplexes for highly nonlinear functions, such as fourth-order polynomials.
To allocate memory for the vector returned by the “nlc” module argument, you must specify the total number of nonlinear constraints with the tenth element of the opt argument. If any of the constraints are equality constraints, the number of equality constraints must be specified by the eleventh element of the opt argument. See the section Parameter Constraints for details.
For more information about the special sets of termination criteria used by the NLPNMS algorithms, see the section Termination Criteria.
In addition to the standard iteration history, the NLPNMS subroutine prints the following information. For unconstrained or boundary-constrained problems, the subroutine also prints the following:
-
difcrit, which, in this subroutine, refers to the difference between the largest and smallest function values of the
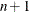 simplex vertices
simplex vertices
-
std, which is the standard deviation of the function values of the simplex vertices
-
deltax, which is the vertex length of a restarted simplex. If there are convergence problems, the algorithm restarts the iteration process with a simplex of smaller vertex length.
-
size, which is the average
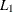 distance of the simplex vertex with the smallest function value to the other simplex vertices
distance of the simplex vertex with the smallest function value to the other simplex vertices
For linearly and nonlinearly constrained problems, the subroutine prints the following:
-
conmax is the maximum constraint violation.
-
meritf is the value of the merit function,
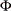 .
.
-
difmerit is the difference between adjacent values of the merit function.
-
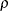 is the trust-region radius.
is the trust-region radius.
The following statements uses the NLPNMS call to solve the Rosen-Suzuki problem (see the section Rosen-Suzuki Problem), which has three nonlinear constraints. Figure 24.236 is a partial listing of the output:
start F_HS43(x);
f = x*x` + x[3]*x[3] - 5*(x[1] + x[2]) - 21*x[3] + 7*x[4];
return(f);
finish F_HS43;
start C_HS43(x);
c = j(3,1,0.);
c[1] = 8 - x*x` - x[1] + x[2] - x[3] + x[4];
c[2] = 10 - x*x` - x[2]*x[2] - x[4]*x[4] + x[1] + x[4];
c[3] = 5 - 2.*x[1]*x[1] - x[2]*x[2] - x[3]*x[3]
- 2.*x[1] + x[2] + x[4];
return(c);
finish C_HS43;
x = j(1, 4, 1);
opt = j(1, 11, .);
opt[2] = 3; opt[10] = 3; opt[11] = 0;
call nlpnms(rc, xres, "F_HS43", x, opt, , , , , "C_HS43");
Figure 24.236: Nelder-Mead Simplex Optimization
| Optimization Start | ||
|---|---|---|
| Parameter Estimates | ||
| N | Parameter | Estimate |
| 1 | X1 | 1.000000 |
| 2 | X2 | 1.000000 |
| 3 | X3 | 1.000000 |
| 4 | X4 | 1.000000 |
| Value of Objective Function = -19 |
| Values of Nonlinear Constraints | |||||
|---|---|---|---|---|---|
| Constraint | Residual | ||||
| [ | 1 | ] | 4.0000 | ||
| [ | 2 | ] | 6.0000 | ||
| [ | 3 | ] | 1.0000 | ||
| Nelder-Mead Simplex Optimization |
| COBYLA Algorithm by M.J.D. Powell (1992) |
| Minimum Iterations | 0 |
|---|---|
| Maximum Iterations | 1000 |
| Maximum Function Calls | 3000 |
| Iterations Reducing Constraint Violation | 0 |
| ABSFCONV Function Criterion | 0 |
| FCONV Function Criterion | 2.220446E-16 |
| FCONV2 Function Criterion | 1E-6 |
| FSIZE Parameter | 0 |
| ABSXCONV Parameter Change Criterion | 0.0001 |
| XCONV Parameter Change Criterion | 0 |
| XSIZE Parameter | 0 |
| ABSCONV Function Criterion | -1.34078E154 |
| Initial Simplex Size (INSTEP) | 0.5 |
| Singularity Tolerance (SINGULAR) | 1E-8 |
| Nelder-Mead Simplex Optimization |
| COBYLA Algorithm by M.J.D. Powell (1992) |
| Parameter Estimates | 4 |
|---|---|
| Nonlinear Constraints | 3 |
| Optimization Start | |||
|---|---|---|---|
| Objective Function | -29.5 | Maximum Constraint Violation | 4.5 |
| Iteration | Restarts | Function Calls |
Objective Function |
Maximum Constraint Violation |
Merit Function |
Merit Function Change |
Ratio Between Actual and Predicted Change |
|
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 12 | -52.80342 | 4.3411 | -42.3031 | 12.803 | 1.000 | |
| 2 | 0 | 17 | -39.51475 | 0.0227 | -39.3797 | -2.923 | 0.250 | |
| 3 | 0 | 53 | -44.02098 | 0.00949 | -43.9727 | 4.593 | 0.0625 | |
| 4 | 0 | 62 | -44.00214 | 0.000833 | -43.9977 | 0.0249 | 0.0156 | |
| 5 | 0 | 72 | -44.00009 | 0.000033 | -43.9999 | 0.00226 | 0.0039 | |
| 6 | 0 | 79 | -44.00000 | 1.783E-6 | -44.0000 | 0.00007 | 0.0010 | |
| 7 | 0 | 90 | -44.00000 | 1.363E-7 | -44.0000 | 1.74E-6 | 0.0002 | |
| 8 | 0 | 94 | -44.00000 | 1.543E-8 | -44.0000 | 5.33E-7 | 0.0001 |
| Optimization Results | |||
|---|---|---|---|
| Iterations | 8 | Function Calls | 95 |
| Restarts | 0 | Objective Function | -44.00000003 |
| Maximum Constraint Violation | 1.543059E-8 | Merit Function | -43.99999999 |
| Actual Over Pred Change | 0.0001 | ||
| ABSXCONV convergence criterion satisfied. |
| Warning: | The point x is feasible only at the LCEPSILON= 1E-7 range. |
| Optimization Results | ||
|---|---|---|
| Parameter Estimates | ||
| N | Parameter | Estimate |
| 1 | X1 | -0.000034167 |
| 2 | X2 | 1.000004 |
| 3 | X3 | 2.000023 |
| 4 | X4 | -0.999971 |
| Value of Objective Function = -44.00000003 |
| Values of Nonlinear Constraints | |||||
|---|---|---|---|---|---|
| Constraint | Residual | ||||
| [ | 1 | ] | -1.54E-8 | *?* | |
| [ | 2 | ] | 1.0000 | ||
| [ | 3 | ] | -1.5E-8 | *?* | |
| The 2 nonlinear constraints which are marked with *?* are not satisfied at the accuracy specified by the LCEPSILON= option. However, the default value of this option seems to be too strong to be applied to nonlinear constraints. |