-
GROUP=effect
GRP=effect
-
defines an effect specifying heterogeneity in the covariance
structure of 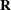 . All observations having the same level of the GROUP effect have the same covariance parameters. Each new level of the GROUP
effect produces a new set of covariance parameters with the same structure as the original group. You should exercise caution
in properly defining the GROUP effect, because strange covariance patterns can result from its misuse. Also, the GROUP effect
can greatly increase the number of estimated covariance parameters, which can adversely affect the optimization process.
. All observations having the same level of the GROUP effect have the same covariance parameters. Each new level of the GROUP
effect produces a new set of covariance parameters with the same structure as the original group. You should exercise caution
in properly defining the GROUP effect, because strange covariance patterns can result from its misuse. Also, the GROUP effect
can greatly increase the number of estimated covariance parameters, which can adversely affect the optimization process.
Continuous variables are permitted as arguments to the GROUP=
option. PROC BTL does not sort by the values of the continuous variable; rather, it considers the data to be from a new subject
or group whenever the value of the continuous variable changes from the previous observation. Using a continuous variable
decreases execution time for models with a large number of subjects or groups and also prevents the production of a large
“Class Levels Information” table.
-
LDATA=SAS-data-set
-
reads the coefficient matrices associated with the TYPE=LIN(number ) option. The data set must contain the variables PARM, ROW, COL1–COLn, or PARM, ROW, COL, VALUE. The PARM variable denotes
which of the number coefficient matrices is currently being constructed, and the ROW, COL1–COLn, or ROW, COL, VALUE variables specify the matrix
values, as they do with the RANDOM statement option GDATA=. Unspecified values of these matrices are set equal to 0.
-
LOCAL
LOCAL=EXP(<effects>)
LOCAL=POM(POM-data-set )
-
requests that a diagonal matrix be added to 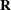 . With just the LOCAL option, this diagonal matrix equals
. With just the LOCAL option, this diagonal matrix equals 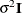 , and
, and 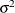 becomes an additional variance parameter that PROC BTL profiles out of the likelihood provided that you do not specify the
NOPROFILE option in the PROC BTL statement. The LOCAL option is useful if you want to add an observational error to a time
series structure (Jones and Boadi-Boateng, 1991) or a nugget effect to a spatial structure (Cressie, 1991).
becomes an additional variance parameter that PROC BTL profiles out of the likelihood provided that you do not specify the
NOPROFILE option in the PROC BTL statement. The LOCAL option is useful if you want to add an observational error to a time
series structure (Jones and Boadi-Boateng, 1991) or a nugget effect to a spatial structure (Cressie, 1991).
The LOCAL=EXP(<effects> ) option produces exponential local effects, also known as dispersion effects, in a log-linear variance model. These local
effects have the form
where 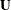 is the full-rank design matrix corresponding to the effects that you specify, and
is the full-rank design matrix corresponding to the effects that you specify, and 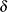 are the parameters that PROC BTL estimates. An intercept is not included in
are the parameters that PROC BTL estimates. An intercept is not included in 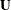 because it is accounted for by
because it is accounted for by 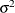 . PROC BTL constructs the full-rank
. PROC BTL constructs the full-rank 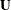 in terms of 1s and
in terms of 1s and  1s for classification effects. Be sure to scale continuous effects in
1s for classification effects. Be sure to scale continuous effects in 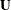 sensibly.
sensibly.
The LOCAL=POM(POM-data-set ) option specifies the power-of-the-mean structure. This structure possesses a variance of the form 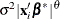 for the
for the 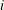 th observation, where
th observation, where 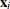 is the
is the 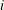 th row of
th row of 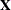 (the design matrix of the fixed effects), and
(the design matrix of the fixed effects), and 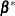 is an estimate of the fixed-effects parameters that you specify in POM-data-set.
is an estimate of the fixed-effects parameters that you specify in POM-data-set.
The SAS data set specified by POM-data-set contains the numeric variable Estimate (in previous releases, the variable name was required to be EST), and it has at least
as many observations as there are fixed-effects parameters. The first 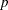 observations of the Estimate variable in POM-data-set are taken to be the elements of
observations of the Estimate variable in POM-data-set are taken to be the elements of 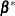 , where
, where 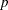 is the number of columns of
is the number of columns of 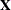 . You must order these observations according to the non-full-rank parameterization of the BTL procedure.
. You must order these observations according to the non-full-rank parameterization of the BTL procedure.
-
LOCALW
-
specifies that only the local effects and no others be weighted. By default, all effects are weighted. The LOCALW option is
used in connection with the WEIGHT statement and the LOCAL option in the REPEATED statement.
-
NONLOCALW
-
specifies that only the nonlocal effects and no others be weighted. By default, all effects are weighted. The NONLOCALW option
is used in connection with the WEIGHT statement and the LOCAL option in the REPEATED statement.
-
SUBJECT=effect
SUB=effect
-
identifies the subjects in your mixed model. Complete independence is assumed across subjects; therefore, the SUBJECT= option
produces a block-diagonal structure in 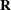 with identical blocks. When the SUBJECT= effect consists entirely of classification variables, the blocks of
with identical blocks. When the SUBJECT= effect consists entirely of classification variables, the blocks of 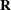 correspond to observations sharing the same level of that effect. These blocks are sorted according to this effect as well.
correspond to observations sharing the same level of that effect. These blocks are sorted according to this effect as well.
Continuous variables are permitted as arguments to the SUBJECT= option. PROC BTL does not sort by the values of the continuous
variable; rather, it considers the data to be from a new subject or group whenever the value of the continuous variable changes
from the previous observation. Using a continuous variable decreases execution time for models with a large number of subjects
or groups.
If you want to model nonzero covariance among all of the observations in your SAS data set, specify SUBJECT=INTERCEPT to treat
the data as if they are all from one subject. However, be aware that, in this case, PROC BTL manipulates an 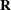 matrix with dimensions equal to the number of observations. If no SUBJECT= effect is specified, then every observation is
assumed to be from a different subject and
matrix with dimensions equal to the number of observations. If no SUBJECT= effect is specified, then every observation is
assumed to be from a different subject and 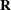 is assumed to be diagonal. For this reason, you usually want to use the SUBJECT= option in the REPEATED statement.
is assumed to be diagonal. For this reason, you usually want to use the SUBJECT= option in the REPEATED statement.
-
TYPE=covariance-structure
-
specifies the covariance structure of the 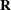 matrix. The SUBJECT= option defines the blocks of
matrix. The SUBJECT= option defines the blocks of 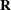 , and the TYPE= option specifies the structure of these blocks. The default structure is VC. See PROC MIXED for details about
the available covariance structures.
, and the TYPE= option specifies the structure of these blocks. The default structure is VC. See PROC MIXED for details about
the available covariance structures.
![]() matrix in the mixed model. Its syntax is different from that of the REPEATED statement in PROC GLM. If no REPEATED statement
is specified,
matrix in the mixed model. Its syntax is different from that of the REPEATED statement in PROC GLM. If no REPEATED statement
is specified, ![]() is assumed to be equal to
is assumed to be equal to ![]() .
.
![]() and use the TYPE= option to define their covariance structure. In this case, the repeated measures data must be similarly
ordered for each subject, and you must indicate all missing response variables with periods in the input data set unless they
all fall at the end of a subject’s repeated response profile. These requirements are necessary in order to inform PROC BTL
of the proper location of the observed repeated responses.
and use the TYPE= option to define their covariance structure. In this case, the repeated measures data must be similarly
ordered for each subject, and you must indicate all missing response variables with periods in the input data set unless they
all fall at the end of a subject’s repeated response profile. These requirements are necessary in order to inform PROC BTL
of the proper location of the observed repeated responses.
![]() corresponding to the observations with the same level. This results in a singular
corresponding to the observations with the same level. This results in a singular ![]() and an infinite likelihood.
and an infinite likelihood.
![]() for each subject are constructed in the order in which they appear in the input data set.
for each subject are constructed in the order in which they appear in the input data set.
