RANDOM Statement :: SAS/Genetics(TM) 12.3 User's Guide

RANDOM Statement

RANDOM random-effects </ options> ;

The RANDOM statement defines the random effects constituting the $\bgamma$ vector in the mixed model. It can be used to specify traditional variance component models (as in the VARCOMP procedure) and to specify random coefficients. The random effects can be classification or continuous variables, and multiple RANDOM statements are possible.

The purpose of the RANDOM statement is to define the $\bZ$ matrix of the mixed model, the random effects in the $\bgamma$ vector, and the structure of $\bG$ . The $\bZ$ matrix is constructed exactly like the $\bX$ matrix for the fixed effects, and the $\bG$ matrix is constructed to correspond with the effects constituting $\bZ$ . The structure of $\bG$ is defined by using the TYPE= option .

You can specify INTERCEPT (or INT) as a random effect to indicate the intercept. PROC BTL does not include the intercept in the RANDOM statement by default as it does in the MODEL statement.

You can specify the following options in the RANDOM statement after a slash (/).

GDATA=SAS-data-set

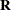requests that the $\bG$ matrix be read in from a SAS data set. This $\bG$ matrix is assumed to be known; therefore, only $\bR$ -side parameters from effects in the REPEATED statement are included in the Newton-Raphson iterations. If no REPEATED statement is specified, then only a residual variance is estimated.

The information in the GDATA= data set can appear in one of two ways. The first is a sparse representation for which you include ROW, COL, and VALUE variables to indicate the row, column, and value of $\bG$ . All unspecified locations are assumed to be 0. The second representation is for dense matrices. In it you include ROW and COL1–COLn variables to indicate the row and columns of $\bG$ , which is a symmetric matrix of order n. For both representations, you must specify effects in the RANDOM statement that generate a $\bZ$ matrix that contains n columns.

If you have more than one RANDOM statement, only one GDATA= option is required in any one of them, and the data set you specify must contain the entire $\bG$ matrix defined by all of the RANDOM statements.

If the GDATA= data set contains variance ratios instead of the variances themselves, then use the RATIOS option.

Known parameters of $\bG$ can also be input using the PARMS statement with the HOLD= option.

GROUP=effect GRP=effect

defines an effect specifying heterogeneity in the covariance structure of $\bG$ . All observations having the same level of the group effect have the same covariance parameters. Each new level of the group effect produces a new set of covariance parameters with the same structure as the original group. You should exercise caution in defining the group effect, because strange covariance patterns can result from its misuse. Also, the group effect can greatly increase the number of estimated covariance parameters, which can adversely affect the optimization process.

Continuous variables are permitted as arguments to the GROUP= option. PROC BTL does not sort by the values of the continuous variable; rather, it considers the data to be from a new subject or group whenever the value of the continuous variable changes from the previous observation. Using a continuous variable decreases execution time for models with a large number of subjects or groups and also prevents the production of a large “Class Levels Information” table.

LDATA=SAS-data-set

reads the coefficient matrices associated with the TYPE=LIN(number ) option. The data set must contain the variables PARM, ROW, COL1–COLn, or PARM, ROW, COL, VALUE. The PARM variable denotes which of the number coefficient matrices is currently being constructed, and the ROW, COL1–COLn, or ROW, COL, VALUE variables specify the matrix values, as they do with the GDATA= option. Unspecified values of these matrices are set equal to 0.

RATIOS

indicates that ratios with the residual variance are specified in the GDATA= data set instead of the covariance parameters themselves. The default GDATA= data set contains the individual covariance parameters.

SUBJECT=effect SUB=effect

identifies the subjects in your mixed model. Complete independence is assumed across subjects; thus, for the RANDOM statement, the SUBJECT= option produces a block-diagonal structure in $\bG$ with identical blocks. The $\bZ$ matrix is modified to accommodate this block-diagonality. In fact, specifying a subject effect is equivalent to nesting all other effects in the RANDOM statement within the subject effect.

Continuous variables are permitted as arguments to the SUBJECT= option. PROC BTL does not sort by the values of the continuous variable; rather, it considers the data to be from a new subject or group whenever the value of the continuous variable changes from the previous observation. Using a continuous variable decreases execution time for models with a large number of subjects or groups.

When you specify the SUBJECT= option and a classification random effect, computations are usually much faster if the levels of the random effect are duplicated within each level of the SUBJECT= effect.

TYPE=covariance-structure

specifies the covariance structure of $\bG$ . Although a variety of structures are available, most applications call for either TYPE=VC or TYPE=UN. The TYPE=VC (variance components) option is the default structure, and it models a different variance component for each random effect.

The TYPE=UN (unstructured) option is useful for correlated random coefficient models. For example,

   random intercept age / type=un subject=person;

specifies a random intercept-slope model that has different variances for the intercept and slope and a covariance between them. You can also use TYPE=FA0(2) here to request a $\bG$ estimate that is constrained to be nonnegative definite.

If you are constructing your own columns of $\bZ$ with continuous variables, you can use the TYPE=TOEP(1) structure to group them together to have a common variance component. If you want to have different covariance structures in different parts of $\bG$ , you must use multiple RANDOM statements with different TYPE= options.

The BTL Procedure (Experimental)

RANDOM Statement