The BTL Procedure (Experimental)
Example 4.1 Performing BTL Model Selection and Estimation
In the following data taken from Coffman et al. (2005), a sample of trout from an experimental backcross population were genotyped at markers spanning 38 chromosomes, and the disease resistance of each trout was recorded concomitantly. In a prior analysis, single-marker tests were performed with each marker, and the marker most strongly associated with the trait for each chromosome was kept. This reduced set of data along with the corresponding map data is input in the following code. "A" corresponds to the homozygous genotype, and "B" corresponds to the heterozygous genotype; these are the default values for PROC BTL.
data TroutDat; input (m1-m17) ($) trait; datalines; A A A B A A B B A A A B B A A B A 0 A B A A B B A B A A A A B B A A B 0 ... more lines ... B B A B B A B A B B A B A B B B B 1 B B B A A B A B A A A A A A A B A 1 ;
data TroutMap; input marker $ location name $ chromosome; datalines; m1 0 agcagc3 1 m2 0 acgatt11 2 m3 0 agcagc5 3 m4 11.6 agcagc6 4 m5 0 accaag22 5 m6 0 agcaca5 6 m7 43 agcagt27 7 m8 9.3 acgagt8 8 m9 52.8 agcact10 9 m10 2.3 agccag11 10 m11 0 accatc3 11 m12 0 accaag8 12 m13 14 accaag13 13 m14 7 acgaag8 14 m15 7 acgatc9 15 m16 0 agcagt26 16 m17 18.4 acccca20 17 ;
First, the single-marker models are tested as shown in the following code. The ALL=1 option in the MARKER statement requests the single-marker model tests for each marker in the MARKER statement. The GROUP= option indicates that chromosome is the linkage group variable in the map data set.
proc btl data=TroutDat map=TroutMap; marker m1-m17 /all=1 group=chromosome; model trait; run;
The single-marker model results are shown in Output 4.1.1.
| Model Statistics | ||||||||
|---|---|---|---|---|---|---|---|---|
| Linkage Group |
Marker Effect |
Name | DF | Chi- Square |
Pr > ChiSq | AIC | AICC | BIC |
| 1 | M1 | agcagc3 | 1 | 2.9479 | 0.0860 | 48.3 | 49.1 | 52.6 |
| 2 | M2 | acgatt11 | 1 | 1.0612 | 0.3029 | 50.1 | 51.0 | 54.4 |
| 3 | M3 | agcagc5 | 1 | 2.9479 | 0.0860 | 48.3 | 49.1 | 52.6 |
| 4 | M4 | agcagc6 | 1 | 2.1504 | 0.1425 | 49.0 | 49.9 | 53.3 |
| 5 | M5 | accaag22 | 1 | 1.2346 | 0.2665 | 50.0 | 50.9 | 54.3 |
| 6 | M6 | agcaca5 | 1 | 1.6173 | 0.2035 | 49.6 | 50.5 | 53.9 |
| 7 | M7 | agcagt27 | 1 | 3.5413 | 0.0599 | 47.7 | 48.5 | 52.0 |
| 8 | M8 | acgagt8 | 1 | 1.2158 | 0.2702 | 50.0 | 50.9 | 54.3 |
| 9 | M9 | agcact10 | 1 | 3.5413 | 0.0599 | 47.7 | 48.5 | 52.0 |
| 10 | M10 | agccag11 | 1 | 2.9479 | 0.0860 | 48.3 | 49.1 | 52.6 |
| 11 | M11 | accatc3 | 1 | 1.2848 | 0.2570 | 49.9 | 50.8 | 54.2 |
| 12 | M12 | accaag8 | 1 | 7.3678 | 0.0066 | 43.8 | 44.7 | 48.1 |
| 13 | M13 | accaag13 | 1 | 5.1787 | 0.0229 | 46.0 | 46.9 | 50.3 |
| 14 | M14 | acgaag8 | 1 | 2.6072 | 0.1064 | 48.6 | 49.5 | 52.9 |
| 15 | M15 | acgatc9 | 1 | 1.7060 | 0.1915 | 49.5 | 50.4 | 53.8 |
| 16 | M16 | agcagt26 | 1 | 2.3491 | 0.1254 | 48.8 | 49.7 | 53.2 |
| 17 | M17 | acccca20 | 1 | 3.5413 | 0.0599 | 47.7 | 48.5 | 52.0 |
Next, all two-marker models are estimated with the following code. Note that only the five best models are requested using the BEST= option, and the model selection criterion is selected to be the 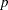 -value from using the MC= option.
-value from using the MC= option.
proc btl data=TroutDat map=TroutMap; marker m1-m17 /all=2 best=5 mc=p group=chromosome; model trait; run;
The two-marker model results are shown in the Output 4.1.2.
| Model Statistics | ||||||
|---|---|---|---|---|---|---|
| Marker Effect |
DF | Chi- Square |
Pr > ChiSq | AIC | AICC | BIC |
| M12*M17 | 3 | 24.8422 | <.0001 | 30.4 | 32.8 | 37.5 |
| M12*M14 | 3 | 15.1226 | 0.0017 | 40.1 | 42.5 | 47.2 |
| M8*M12 | 3 | 13.6663 | 0.0034 | 41.5 | 43.9 | 48.7 |
| M7*M12 | 3 | 12.9359 | 0.0048 | 42.3 | 44.7 | 49.4 |
| M9*M12 | 3 | 11.6006 | 0.0089 | 43.6 | 46.0 | 50.8 |
It looks like m12 xm17 is the best two-marker effect. You can try to estimate parameters for a BTL model by using the following code. The parameter estimation is requested using the PARMEST statement. The linkage units of the location variable from the map data set are specified to be CM (centimorgans) by using the LINKUNIT option. The linkage model used to create the inputted linkage map is specified as Haldane by using the LINKMOD= option.
Now that the experimental design has been specified, by default PROC BTL performs a grid search over a range of possible recombination values and displays penetrance estimates that are found to be within the range of valid values. The default grid search for the  uses values from 0 to 0.5 in increments of 0.1. In the following code, a finer grid search is requested by specifying the increment to be 0.05 in the RINC= option. Also, the penetrance parameter limits are set to be –0.1 and 1.1 using the options PMIN= and PMAX=, respectively (the default values are 0 and 1). The SAS code follows.
uses values from 0 to 0.5 in increments of 0.1. In the following code, a finer grid search is requested by specifying the increment to be 0.05 in the RINC= option. Also, the penetrance parameter limits are set to be –0.1 and 1.1 using the options PMIN= and PMAX=, respectively (the default values are 0 and 1). The SAS code follows.
proc btl data=TroutDat map=TroutMap; marker m12 m17 /group=chromosome; model trait; parmest r=0 linkmod=H linkunit=cm boot=1000; run;
The average penetrance value for each marker class is shown in the "Marker Class Means" table in Output 4.1.3, and the BTL penetrance estimates found using 0 for the marker-BTL recombination rates are shown in the "Parameter Estimates" table in Output 4.1.4. The confidence limits for the penetrance parameters from using the bootstrap technique are displayed in Output 4.1.4 as well.
| Marker Class Means | ||||
|---|---|---|---|---|
| Marker Class |
Marker Genotype |
N | Mean | Standard Error |
| pi11 | AA | 8 | 1.0000 | 0.0000 |
| pi12 | AB | 8 | 0.2500 | 0.0234 |
| pi21 | BA | 6 | 0.0000 | 0.0000 |
| pi22 | BB | 9 | 0.3333 | 0.0247 |
| Parameter Estimates | |||
|---|---|---|---|
| Parameter | Estimate | 95% Confidence Limits | |
| r1 | 0.0000 | ||
| r2 | 0.0000 | ||
| p11 | 4.0000 | 4.0000 | 4.0000 |
| p12 | 1.0000 | 0.0000 | 2.4000 |
| p21 | 0.0000 | 0.0000 | 0.0000 |
| p22 | 1.3333 | 0.0000 | 2.6667 |
| theta | 0.5000 | ||
| NOTE: The r and theta parameters are fixed. |
|||
Suppose your input data were coded differently, and "A" signified heterozygote and "B" signified homozygote. Since this coding is different from the default, you can specify the genotype values by using the HOMOZYGOTE= (or HO=) and HETEROZYGOTE= (or HE=) options.
proc btl data=TroutDat map=TroutMap; marker m12 m17 /group=chromosome; model trait; parmest ho="B" he="A" r=0 linkmod=H linkunit=cm boot=1000; run;
In Outputs 4.1.5 and 4.1.6, notice that the marker class mean values are reversed and different penetrance estimates are obtained.
| Marker Class Means | ||||
|---|---|---|---|---|
| Marker Class |
Marker Genotype |
N | Mean | Standard Error |
| pi11 | BB | 9 | 0.3333 | 0.0247 |
| pi12 | BA | 6 | 0.0000 | 0.0000 |
| pi21 | AB | 8 | 0.2500 | 0.0234 |
| pi22 | AA | 8 | 1.0000 | 0.0000 |
| Parameter Estimates | |||
|---|---|---|---|
| Parameter | Estimate | 95% Confidence Limits | |
| r1 | 0.0000 | ||
| r2 | 0.0000 | ||
| p11 | 1.3333 | 0.0000 | 2.6667 |
| p12 | 0.0000 | 0.0000 | 0.0000 |
| p21 | 1.0000 | 0.0000 | 2.4000 |
| p22 | 4.0000 | 4.0000 | 4.0000 |
| theta | 0.5000 | ||
| NOTE: The r and theta parameters are fixed. |
|||
Note: This procedure is experimental.
