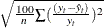The SIMLIN Procedure
Printed Output
Structural Form
The following items are printed as they are read from the EST= input data set. Structural zeros are printed as dots in the listing of these matrices.
-
Structural Coefficients for Endogenous Variables. This is the G matrix, with g rows and g columns.
-
Structural Coefficients for Lagged Endogenous Variables. These coefficients make up the C matrix, with g rows and l columns.
-
Structural Coefficients for Exogenous Variables. These coefficients make up the B matrix, with g rows and k columns.
Reduced Form
-
The reduced form coefficients are obtained by inverting G so that the endogenous variables can be directly expressed as functions of only lagged endogenous and exogenous variables.
-
Inverse Coefficient Matrix for Endogenous Variables. This is the inverse of the G matrix.
-
Reduced Form for Lagged Endogenous Variables. This is

 =G
=G 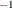 C, with g rows and l columns. Each value is a dynamic multiplier that shows how past values of lagged endogenous variables affect values of each
of the endogenous variables.
C, with g rows and l columns. Each value is a dynamic multiplier that shows how past values of lagged endogenous variables affect values of each
of the endogenous variables.
-
Reduced Form for Exogenous Variables. This is

 =G
=G  B, with g rows and k columns. Its values are called impact multipliers because they show the immediate effect of each exogenous variable on the value of the endogenous variables.
B, with g rows and k columns. Its values are called impact multipliers because they show the immediate effect of each exogenous variable on the value of the endogenous variables.
Multipliers
Interim and total multipliers show the effect of a change in an exogenous variable over time.
-
Interim Multipliers. These are the interim multiplier matrices. They are formed by multiplying

 by powers of D. The dth interim multiplier is D
by powers of D. The dth interim multiplier is D 

 . The interim multiplier of order d shows the effects of a change in the exogenous variables after d periods. Interim multipliers are only available if the maximum lag of the endogenous variables is 1.
. The interim multiplier of order d shows the effects of a change in the exogenous variables after d periods. Interim multipliers are only available if the maximum lag of the endogenous variables is 1.
-
Total Multipliers. This is the matrix of total multipliers, T=(I-D )

 . This matrix shows the cumulative effect of changes in the exogenous variables. Total multipliers are only available if the
maximum lag is one.
. This matrix shows the cumulative effect of changes in the exogenous variables. Total multipliers are only available if the
maximum lag is one.
Statistics of Fit
If the DATA= option is used and the DATA= data set contains endogenous variables, PROC SIMLIN prints a statistics-of-fit report
for the simulation. The statistics printed include the following. (Summations are over the observations for which both 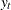 and
and 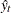 are nonmissing.)
are nonmissing.)
-
the number of nonmissing errors. (Number of observations for which both
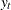 and
and 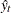 are nonmissing.)
are nonmissing.)
-
the mean error:
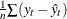
-
the mean percent error:
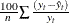
-
the mean absolute error:
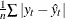
-
the mean absolute percent error
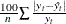
-
the root mean square error:
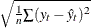
-
the root mean square percent error: