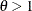The HPCOPULA Procedure
Archimedean Copulas
Overview of Archimedean Copulas
Let function ![$\phi : [0,1] \rightarrow [0, \infty )$](images/etsug_hpcopula0051.png) be a strict Archimedean copula generator function, and suppose that its inverse
be a strict Archimedean copula generator function, and suppose that its inverse 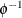 is completely monotonic on
is completely monotonic on 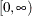 . A strict generator is a decreasing function
. A strict generator is a decreasing function ![$\phi :[0,1]\rightarrow [0, \infty )$](images/etsug_hpcopula0054.png) that satisfies
that satisfies 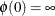 and
and 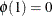 . A decreasing function
. A decreasing function ![$f(t):[a,b]\rightarrow (-\infty ,\infty )$](images/etsug_hpcopula0057.png) is completely monotonic if it satisfies
is completely monotonic if it satisfies
![\[ (-1)^ k \frac{d^ k}{dt^ k} f(t)\ge 0, k\in \mathbb {N}, t\in (a,b) \]](images/etsug_hpcopula0058.png)
An Archimedean copula is defined as follows:
![\[ C(u_1, u_2,\ldots , u_ m) = \phi ^{-1}\Bigl ( \phi (u_1) + \cdots + \phi (u_ m) \Bigr ) \]](images/etsug_hpcopula0059.png)
The Archimedean copulas available in the HPCOPULA procedure are the Clayton copula, the Frank copula, and the Gumbel copula.
Simulation
Suppose that the generator of the Archimedean copula is  . Then the simulation method that uses a Laplace-Stieltjes transformation of the distribution function is given by Marshall
and Olkin (1988), where
. Then the simulation method that uses a Laplace-Stieltjes transformation of the distribution function is given by Marshall
and Olkin (1988), where 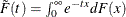 :
:
-
Generate a random variable V that has the distribution function F such that
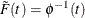 .
.
-
Draw samples from the independent uniform random variables
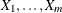 .
.
-
Return
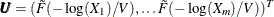 .
.
The Laplace-Stieltjes transformations are as follows:
-
For the Clayton copula,
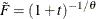 , and the distribution function F is associated with a gamma random variable that has a shape parameter of
, and the distribution function F is associated with a gamma random variable that has a shape parameter of 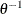 and a scale parameter of 1.
and a scale parameter of 1.
-
For the Gumbel copula,
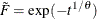 , and F is the distribution function of the stable variable
, and F is the distribution function of the stable variable 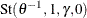 , where
, where ![$\gamma = [\cos (\pi /(2\theta ))]^\theta $](images/etsug_hpcopula0081.png) .
.
-
For the Frank copula where
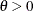 ,
, ![$\tilde{F}= - \log \{ 1-\exp (-t)[1- \exp (-\theta )]\} /\theta $](images/etsug_hpcopula0082.png) , and
, and 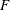 is a discrete probability function
is a discrete probability function 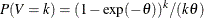 . This probability function is related to a logarithmic random variable that has a parameter value of
. This probability function is related to a logarithmic random variable that has a parameter value of 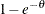 .
.
For more information about simulating a random variable from a stable distribution, see Theorem 1.19 in Nolan (2010). For more information about simulating a random variable from a logarithmic series, see Chapter 10.5 in Devroye (1986).
For a Frank copula where 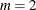 and
and 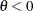 , the simulation can be done through conditional distributions as follows:
, the simulation can be done through conditional distributions as follows:
-
Draw independent
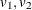 from a uniform distribution.
from a uniform distribution.
-
Let
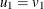 .
.
-
Let
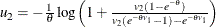 .
.

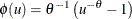
![\[ C_{\theta }(u_1, u_2,{\ldots }, u_ m) = \left[ \sum _{i=1}^ m u_ i^{-\theta } - m+1\right] ^{-1/\theta } \]](images/etsug_hpcopula0061.png)
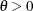
![\[ \phi (u) = - \log \left[ \frac{\exp (-{\theta }u)-1}{\exp (-{\theta })-1}\right] \]](images/etsug_hpcopula0063.png)
![\[ C_{\theta }(u_1, u_2,{\ldots }, u_ m) = \frac{1}{\theta } \log \left\{ 1 + \frac{\prod _{i=1}^{m}[\exp (-{\theta }u_ i)-1]}{[\exp (-{\theta })-1]^{m-1}} \right\} \]](images/etsug_hpcopula0064.png)
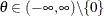
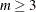
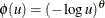
![\[ C_{\theta }(u_1, u_2,{\ldots }, u_ m) = \exp \left\{ - \left[ \sum _{i=1}^{m}(-\log u_ i)^\theta \right] ^{1/{\theta }} \right\} \]](images/etsug_hpcopula0070.png)