The HPCOPULA Procedure

Normal Copula

Subsections:

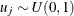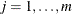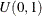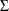Let $u_ j \sim U(0,1)$ for $j=1,\ldots ,m$, where $U(0,1)$ represents the uniform distribution on the $[0,1]$ interval. Let $\Sigma $ be the correlation matrix, where 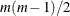$m(m-1)/2$ parameters satisfy the positive semidefiniteness constraint. The normal copula can be written as

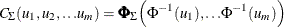
\begin{equation*} C_{\Sigma }(u_1, u_2,{\ldots } u_ m) = \bm {\Phi }_\Sigma \Bigl (\Phi ^{-1} (u_1),{\ldots } \Phi ^{-1} (u_ m)\Bigr ) \end{equation*}

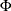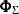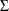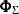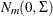where $\Phi $ is the distribution function of a standard normal random variable and $\bm {\Phi }_\Sigma $ is the m-variate standard normal distribution with mean vector 0 and covariance matrix $\Sigma $. That is, the distribution $\bm {\Phi }_\Sigma $ is $N_ m(0,\Sigma )$.

Simulation

For the normal copula, the input of the simulation is the correlation matrix 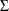$\Sigma $. The normal copula can be simulated by the following steps, in which 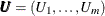$\bm U= (U_1,\ldots ,U_ m)$ denotes one random draw from the copula:

  1. Generate a multivariate normal vector 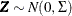$\bm Z \sim N(0,\Sigma )$, where 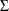$\Sigma $ is an m-dimensional correlation matrix.

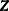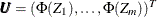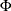  2. Transform the vector $\bm Z$ into $\bm U= (\Phi (Z_1),\ldots ,\Phi (Z_ m))^ T$, where $\Phi $ is the distribution function of univariate standard normal.

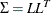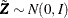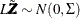The first step can be achieved by Cholesky decomposition of the correlation matrix $\Sigma =LL^ T$, where L is a lower triangular matrix with positive elements on the diagonal. If $\bm {\tilde{Z}} \sim N(0,I)$, then $L\bm {\tilde{Z}} \sim N(0,\Sigma )$.