The PANEL Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesComputational ResourcesRestricted EstimatesNotationOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsBetween EstimatorsPooled EstimatorOne-Way Random-Effects ModelTwo-Way Random-Effects ModelParks Method (Autoregressive Model)Da Silva Method (Variance-Component Moving Average Model)Dynamic Panel EstimatorLinear Hypothesis TestingHeteroscedasticity-Corrected Covariance MatricesHeteroscedasticity- and Autocorrelation-Consistent Covariance MatricesR SquareSpecification TestsPanel Data Poolability TestPanel Data Unit Root TestsTroubleshootingCreating ODS GraphicsOUTPUT OUT= Data SetOUTEST= Data SetOUTTRANS= Data SetPrinted OutputODS Table Names
Missing ValuesComputational ResourcesRestricted EstimatesNotationOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsBetween EstimatorsPooled EstimatorOne-Way Random-Effects ModelTwo-Way Random-Effects ModelParks Method (Autoregressive Model)Da Silva Method (Variance-Component Moving Average Model)Dynamic Panel EstimatorLinear Hypothesis TestingHeteroscedasticity-Corrected Covariance MatricesHeteroscedasticity- and Autocorrelation-Consistent Covariance MatricesR SquareSpecification TestsPanel Data Poolability TestPanel Data Unit Root TestsTroubleshootingCreating ODS GraphicsOUTPUT OUT= Data SetOUTEST= Data SetOUTTRANS= Data SetPrinted OutputODS Table Names -
Example

- References
Da Silva Method (Variance-Component Moving Average Model)
The Da Silva method assumes that the observed value of the dependent variable at the tth time point on the ith cross-sectional unit can be expressed as
|
|
where
-
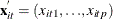 is a vector of explanatory variables for the tth time point and ith cross-sectional unit
is a vector of explanatory variables for the tth time point and ith cross-sectional unit
-
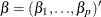 is the vector of parameters
is the vector of parameters
-
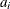 is a time-invariant, cross-sectional unit effect
is a time-invariant, cross-sectional unit effect
-
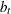 is a cross-sectionally invariant time effect
is a cross-sectionally invariant time effect
-
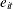 is a residual effect unaccounted for by the explanatory variables and the specific time and cross-sectional unit effects
is a residual effect unaccounted for by the explanatory variables and the specific time and cross-sectional unit effects
Since the observations are arranged first by cross sections, then by time periods within cross sections, these equations can be written in matrix notation as
|
|
where
|
|
|
|
|
|
|
|
|
|
|
|
Here 1 ![]() is an
is an ![]() vector with all elements equal to 1, and
vector with all elements equal to 1, and ![]() denotes the Kronecker product.
denotes the Kronecker product.
The following conditions are assumed:
-
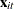 is a sequence of nonstochastic, known
is a sequence of nonstochastic, known 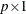 vectors in
vectors in 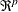 whose elements are uniformly bounded in
whose elements are uniformly bounded in 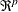 . The matrix X has a full column rank p.
. The matrix X has a full column rank p.
-
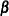 is a
is a 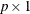 constant vector of unknown parameters.
constant vector of unknown parameters.
-
a is a vector of uncorrelated random variables such that
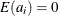 and
and 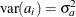 ,
, 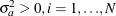 .
.
-
b is a vector of uncorrelated random variables such that
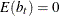 and
and 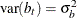 where
where 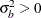 and
and 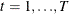 .
.
-
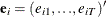 is a sample of a realization of a finite moving-average time series of order
is a sample of a realization of a finite moving-average time series of order 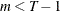 for each i ; hence,
for each i ; hence,
![\[ e_{it}={\alpha }_{0} {\epsilon }_{it}+ {\alpha }_{1} {\epsilon }_{it-1}+{\ldots }+ {\alpha }_{m} {\epsilon }_{it-m} \; \; \; \; t=1,{\ldots },\mi {T} ; i=1,{\ldots },\mi {N} \]](images/etsug_panel0480.png)
where
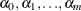 are unknown constants such that
are unknown constants such that  and
and 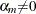 , and
, and 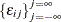 is a white noise process for each
is a white noise process for each 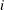 —that is, a sequence of uncorrelated random variables with
—that is, a sequence of uncorrelated random variables with 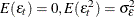 , and
, and 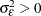 .
. 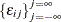 for
for 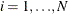 are mutually uncorrelated.
are mutually uncorrelated.
-
The sets of random variables
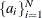 ,
, 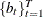 , and
, and 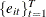 for
for 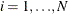 are mutually uncorrelated.
are mutually uncorrelated.
-
The random terms have normal distributions
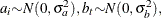 and
and 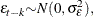 for
for 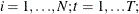 and
and 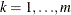 .
.
If assumptions 1–6 are satisfied, then
|
|
and
|
|
where ![]() is a
is a ![]() matrix with elements
matrix with elements ![]() as follows:
as follows:
|
|
where ![]() for
for ![]() . For the definition of
. For the definition of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , see the section Fuller and Battese’s Method.
, see the section Fuller and Battese’s Method.
The covariance matrix, denoted by V, can be written in the form
|
|
where ![]() , and, for k =1,
, and, for k =1,![]() , m,
, m, ![]() is a band matrix whose kth off-diagonal elements are 1’s and all other elements are 0’s.
is a band matrix whose kth off-diagonal elements are 1’s and all other elements are 0’s.
Thus, the covariance matrix of the vector of observations y has the form
|
|
where
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The estimator of ![]() is a two-step GLS-type estimator—that is, GLS with the unknown covariance matrix replaced by a suitable estimator of V. It is obtained by substituting Seely estimates for the scalar multiples
is a two-step GLS-type estimator—that is, GLS with the unknown covariance matrix replaced by a suitable estimator of V. It is obtained by substituting Seely estimates for the scalar multiples ![]() .
.
Seely (1969) presents a general theory of unbiased estimation when the choice of estimators is restricted to finite dimensional
vector spaces, with a special emphasis on quadratic estimation of functions of the form ![]() .
.
The parameters ![]() (i =1,
(i =1,![]() , n) are associated with a linear model E(y )=X
, n) are associated with a linear model E(y )=X ![]() with covariance matrix
with covariance matrix ![]() where
where ![]() (i =1,
(i =1, ![]() , n) are real symmetric matrices. The method is also discussed by Seely (1970a,1970b) and Seely and Zyskind (1971). Seely
and Soong (1971) consider the MINQUE principle, using an approach along the lines of Seely (1969).
, n) are real symmetric matrices. The method is also discussed by Seely (1970a,1970b) and Seely and Zyskind (1971). Seely
and Soong (1971) consider the MINQUE principle, using an approach along the lines of Seely (1969).